In this short series of articles, I’m writing about mathematical questions we don’t know the answer to – which haven’t yet been proven or disproven. This is the second article in the series, and considers a less well-known variant on an extremely well-known problem.
Ask anyone to name a theorem, and they’ll probably come up with one of the really famous ones, like Pythagoras’ theorem. This super-handy hypotenuse fact states that for a triangle with sides A, B and C, where the angle between A and B is a right angle, we have $C^2 = A^2 + B^2$. This leads us on to a nice bit of stamp-collecting – there are infinitely many triples of integers, A, B and C, which fit this equation, called Pythagorean Triples.
One well-known generalisation of this is to change the value $2$ to larger values, and go looking for triples satisfying $C^n = A^n + B^n$. But don’t – Andrew Wiles spent a good chunk of his life on proving that you can’t, for any value of $n>2$, find any such triples. The statement was originally made by Pierre De Fermat, and while Fermat famously didn’t write down a proof, it was the last of his mathematical statements to be gifted one – hence the name ‘Fermat’s Last Theorem’ – and proving it took over 350 years.
This series is of course about the unknown results in mathematics, the mysterious cases of questions we don’t yet have an answer for – so I’ll take you in another direction. If instead of considering these Pythagorean triples as the sides of right angled triangles, we think of them as the sides and diagonal of rectangles (yes, I know that’s the same thing, but bear with me) – we can extend this question into a nice puzzle. These rectangles made from Pythagorean triples will all have all four sides with integer length, and also their diagonal is an integer.
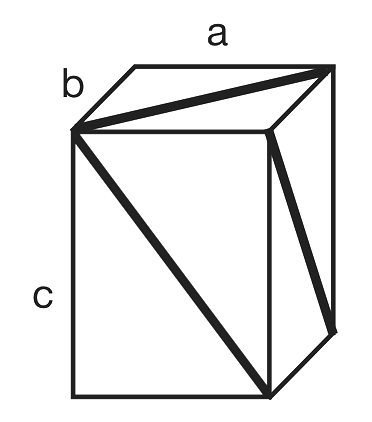
If I want to find not just a rectangle whose sides and diagonals are all integers, but instead a three-dimensional cuboid, with all the side lengths as integers, and additionally the diagonal of each face an integer too, it’s a more difficult question. If you’d like, go away and write down the equations for the lengths of all of these things, and see if you can find a set where all the answers are integers. I’ll hide one possible solution in the image on the right (click on it to see the answers).
Such a cuboid, with all sides and face diagonals having integer length, is known as an Euler Brick. Named after Leonhard Euler, there are infinitely many of these – obviously, since having found one you can multiply all the lengths by an integer and get a larger one. A primitive Euler brick is one for which all the edge lengths are coprime. You can also take an existing Euler brick with edges $(a,b,c)$, and create another one with edges $(bc, ac, ab)$ which will also be an Euler brick.
However, it still hasn’t quite got interesting enough. Some of you may be ahead of me here. If you additionally require the internal corner-to-opposite-corner diagonal of the cuboid, called the space diagonal, to have integer length (I’m going to pause and let you appreciate how good the name ‘space diagonal’ is, for anything, ever) – this restriction creates an object called a perfect cuboid. Again, knock yourself out working out the set of equations you’d need to satisfy. Any perfect cuboid will necessarily also be an Euler brick. But here’s the crazy thing – no known example of a perfect cuboid exists!
According to Wikipedia (as of November 2012), nobody has found any solutions to the equations defining a perfect cuboid. Computer programs have been run which show that if any such cuboid exists, its smallest side must be longer than $10^{10}$ and one of its edges must be longer than $3 \times 10^{12}$. There’s also a nice list on Wikipedia of properties that the edges of a primitive perfect cuboid must satisfy, which are implied by modular arithmetic.
So there you have it! A problem so simple you could explain it to a child, and yet mathematics is stumped. Maybe a perfect cuboid will be found by someone, with a big enough computer, in our lifetimes. Perhaps, with enough mathematical ingenuity, someone will prove that there’s no such thing. Or maybe, if we’re really lucky, someone will find a use for all this. But that’s just a pipe dream.
References:
Fermat’s Last Theorem, on Wikipedia
Perfect Cuboid, at Wolfram Mathworld
I feel a very strong affinity with these cuboids, for a reason I can’t quite put a name to.
Another very easy to understand mathematical problem, but extremely hard to solve. This kind of stuff made me interested in mathematics when I was a child. I have tried to brute force this problem too with maximum side length < 10⁸ and no solution of course.
This is another good page about the the perfect cuboid and closely related problems:
http://www.christianboyer.com/eulerbricks/
As of March 10, 2013 (after quite a few CPU years of run time) I have confirmed that there are no perfect cuboids with odd side length less than 5 trillion (5 x 10^12). –Rob
Hi Rob:
Over the past few years I have found 36830 different primitive body cuboids, and of these 3725 have odd edge larger than 10^13. I would be interested in knowing how many different primitive body cuboids you have found with odd edge less than 5 x 10^12. How many less than 10^12 ? 10^11? 10^10 ? . . . This would help me judge how complete my data files are. My present counts are
10^2 1
10^3 11
10^4 39
10^5 120
10^6 416
10^7 1164
10^8 2997
10^9 6858
10^10 13479
10^11 21514
10^12 28454
10^13 33105
10^14 35738
10^15 36817
10^16 36830
I’m reasonably sure about the counts up to 10^6, while 10^7 may be one or two short. After that there are more and more primitives yet to be found by my search method.
Hi Terry — Believe it or not, just now seeing your post 15 months after the fact. Unfortunately, I don’t have an answer for you. My method for searching for odd-side perfect cuboids (and for that matter even-side) does not facilitate reporting of body cuboids. (It searches for cases where the sum of the squares of two Pythagorean triple solutions for a given odd side match the square of a third solution). Btw, my searches have exhaustively checked the minimum odd side for a primitive perfect cuboid up to 25 trillion, and the minimum even side up to 2 trillion (which means the overall minimum side of a primitive perfect cuboid must be greater than 2 trillion).
Would a solution to the perfect cuboid problem actually make any kind of difference, I mean other than to perhaps offer some kind of closure to mathematicians who may have spent some amount of their spare time trying to solve it?
You never know! I wouldn’t be surprised to see it have an application somewhere in computing, or some funky geometry.
It seems unlikely, but, as Christian says, you never know. You only have to recall that it was just a few years ago that everyone thought the search for huge prime numbers was completely pointless, a trivial waste of time and resources. Now, because of the vital role that large primes play in the fields of cryptography and internet security, this research is seen as absolutely fundamental, and attracts literally billions of dollars of funding from governments and corporations!
To me there appears to be no solution to this problem (no perfect cuboid). In fact, I would propose the following conjecture:
if a^2 + d^2 = g^2 = b^2 + e^2 where a, b are sides and d and e are the diagonal lengths of those two sides, then the only solution for a, b, d, e and g very g is the trivial solution of a=0, d=0 or a=b,d=e or a=e,d=b.
I can’t prove it, but essentially the third side adds absolutely nothing to the problem since g appearing in the equation I have described includes the side c already. g is formed on the basis of a, b and c, so c is essentially a free variable.
Such a cuboid doesn’t exist . And I can prove this.
Neelam: if you can, you will be the first since problem was first proposed over 3 centuries ago.