Since I haven’t written a MathsJam recap for a few months, due to extreme busyness, this post will recap things which happened at December’s MathsJam as well as some other things I found in the pile of scrap paper when I went to tidy it all away over New Year.

December’s MathsJam meetings were moved forward a week, since we thought people might not turn up to one held on Christmas Eve (since they’d all be at midnight maths anyway) so we met on 17th – still sufficiently near Christmas to be Christmassy, and so people brought along mince pies and various other baked goods, including some Mars bar and marshmallow rice crispie cakes, which disappeared mysteriously quickly.

The main focus of the evening was the building of a fractal Christmas tree, based on the worksheets from the Think Maths website. The worksheets allow you to print nets of a Sierpinski tetrahedron, Menger sponge and Koch snowflake, which can be repeated to whatever extent you deem necessary and then assembled into a festive-looking tree. Our effort was a decent size, and the @MathsJam twitter feed from around then contains some photos of the tree as well as a video of it zooming outwards like a true fractal.

We printed the worksheets at A5 size, which meant the tetrahedra and Menger sponge weren’t quite the right size relative to each other that the hole in the base of the tetrahedron wasn’t bigger than the face of the cube – it meant the top part balanced quite precariously, but I’m not completely sure we changed the relative scales by printing them both with the area scaled down, and if anyone can work out whether it’d be different using A4 versions, let me know.

We wondered how the next scale up would work – making $64 \times 4 = 256$ tetrahedra would leave a huge hole in the base, and would this be able to balance on a Menger sponge made from 20 of the Menger sponges (3 times as long on each side)? I’ve seen it done using three sponges, one under each smaller tree, but one big one would be better. It also just occurred to me that the really hardcore way to scale up the Koch snowflake on the top would be to cut 20 and staple them into an icosahedron. We did not do that.

Extreme props to Mark, who spent a good chunk of time cutting out the Koch snowflake for the top of the tree. He cut the tiny triangles out, where the other two faces were cut by people who cut them off, so we nominated this the front of the tree. Around that time, Leeds MathsJam were discussing on Twitter how to fold a piece of paper so as to make a Koch snowflake with a single cut. That would certainly have saved some time – unless you wanted an infinitely detailed snowflake, in which case it might take longer to do the folding. Than the life of the universe.

Afterwards, we donated our completed tree to the pub, which they were immensely pleased with. We spent a small fraction of our MathsJam being jealous of Leeds MathsJam, whose pub had not only decorated the blackboard (blackboard!!) to welcome them, but also provided them with crackers and mince pies.

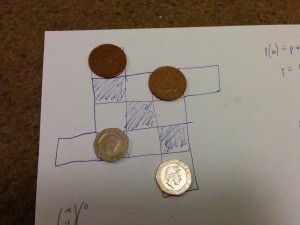We moved on to some other puzzles, including a coins/knight’s moves puzzle tweeted by a mystery MathsJam, which later turned out to be Nottingham. Given the layout of board and coins shown in the photo, what’s the minimum number of knight’s moves needed to switch the two silver coins for the copper ones?

Another discussion centred around this probability puzzle: Two people take turns to roll a dice, and on each roll, if they roll a 6 they win and if not the game continues. Is this game fair, and if not which player has the advantage?

There’s a nice way to show this using probability trees, but some of us managed without even drawing one. We then discussed the further question: if the game isn’t fair (which the existence of this further question slightly implies), what would you need the probability of winning on each go to be in order to make it fair? Is it even possible to do that? We hacked around at it and convinced ourselves of an answer.

We also spent a while discussing the five card trick (another explanation) by mathematician William Fitch Cheney, Jr., where a spectator randomly chooses five cards from a deck, and two magicians have agreed a system whereby if one magician passes the other four of the cards, the other can name the fifth. It’s a lovely trick, and several variations have been developed, many of which are discussed in Colm Mulcahy’s recent book.

According to Twitter, we also discussed Doctor Who, and the best way to teach coding (we concluded people should be able to pseudocode well, as a priority over knowing a load of syntax). I can’t find anything else illuminating from December’s Jam, but here are some other puzzles I found lurking in the scrap paper pile (apologies if these aren’t correctly stated, but I’m reconstructing the questions from someone’s scribbled solutions):

• Given a cube made from smaller cubelets ($n \times n \times n$), if you remove all the cubelets along one edge, prove that the number of cubelets remaining will be divisible by six.
• Given a pile of 105 rocks split into piles of 51, 49 and 5, you’re allowed to either combine two piles or split an even pile in half. Can you achieve 105 piles of size 1?
• Can you arrange 11 trees on a field to maximise the number of possible lines which pass through three or more trees? What’s the most lines you can make?
• Given a $3 \times 3$ grid of squares, and a cube whose face is the same size as one of the small squares, can you cut the grid along some of the gridlines and use it to wrap the cube so all the faces are covered?
• The Hadwiger-Nelson problem: what’s the minimum number of colours needed to colour the whole plane so that no two points which are distance 1 apart are the same colour?

That’s all for this month – the next MathsJam is on Tuesday 21st January, at a pub near your house. Go and join in!