This year has been frankly ridiculous. And while we’ve done our best to cover all the hot maths topics throughout, we have inevitably missed a few. Here’s some mathematical news bits and bobs from 2016 which we (and you!) may have not noticed.
Scottish Open uses mathematical formulae to number golf holes
Tomorrows pin flags at the #AAMSO will have a slight twist! See if you can work them out #JustForFun @MathsScot pic.twitter.com/6AlMGZ503v
— AAM Scottish Open (@AAMScottishOpen) July 5, 2016
Katie: This year, instead of the standard 1 to 18 written on the flags, the Scottish Open Golf Tournament used simple mathematical formulae – such as $12-7$ or $2^3 + 2^3$ to label their holes. It was a fun twist, and the tweet mentions @MathsScot – the Scottish government’s Making Maths Count campaign, which I suppose means they may have been involved.
Inference: International Review of Science
CLP: A while ago we received an email from the marketing director of an online journal titled “Inference: International Review of Science”. All of our fake-journal alarm bells immediately started ringing.
Surprisingly, Inference is not a journal with dubious standards of peer review set up to diddle authors out of publishing fees – it’s a marvellous scholarly review of the sciences, from a humanist perspective, like an even more high-brow Nautilus magazine.
The email suggested we might like an article by Alexander Kharazishvili about Cantor’s diagonalisation method. While it looks at first glance like the same potted history of formal logic that you might have seen a hundred times before, they’re not afraid of a bit of notation, and in fact it goes into a lot of depth – it’s a real review of the subject. Kharazishvili has written another article for Inference, about divergent sequences, which I prefer even though it contains the phrase “the proof is easy”.
They’ve got some big names to write for them – to name one, Gregory Chaitin has written an article about experimental/empirical mathematics.
Inference: International Review of Science
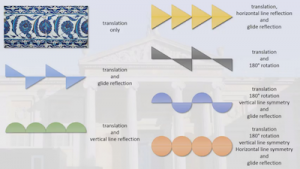Random Walks – the Mathematics of the Ashmolean
Katie: Mathematicians from the University of Oxford Mathematical Institute have teamed up with the Ashmolean museum to produce a series of films demonstrating the mathematics behind the museum’s historical artefacts. From Babylonian tablets to symmetrical tile patterns, there are three 6-8 minute films, plus one that introduces the whole series.
Random Walks – the Mathematics of the Ashmolean, at the Univeristy of Oxford website
Fermat’s Library
CLP: Fermat’s Library is like a big online journal club – they post a paper that somebody has suggested, and then readers are free to annotate and comment on it.
The community seems to comprise a large contingent of Silicon Valley types, so the papers posted tend towards the kind of thing they enjoy, but there’s some maths.
The interface is beautiful, and very well designed – comments are denoted by little dots positioned just off the margins of the paper, and open up into a sidebar that can display images, equations, or even videos. There’s also a traditional comments thread at the bottom for discussion of the paper as a whole.
I’ve had this link saved in my inbox since January of this year because I really wanted to do a proper treatment of it, but never got round to it. Sadly, it seems like not too many people use the site – most of the papers I’ve looked at only have annotations from one person, although they’re almost always of a high quality.
Thanks to Aperiodifan Nathan Day for sending this in. He said, “as an A-level student who wouldn’t otherwise understand most of the papers, I have found it really interesting and useful to have these papers explained and suggested to me each week.”
How the Circle Line rogue train was caught with data
Katie: Back at the start of December, we found this nice story about one of the train lines in Singapore’s underground system on which the trains weren’t behaving themselves, and how they used data analysis to figure out what was going on.
How the Circle Line rogue train was caught with data, at the data.gov.sg blog
Fermat’s Library
17 mathematical GIFs that are either deeply soothing or will make you understand maths (or both)
Katie: Buzzfeed have collected a set of mathematically interesting GIF animations (just under half of which are from @solvemymaths’ Twitter feed), including images from geometry, fractals, trig and data vis. The title of the article and the post URL seem to disagree on whether they’re deeply soothing or will make you understand maths, but I’m enjoying them either way.
17 Mathematical GIFs That Are Deeply Soothing, at Buzzfeed
A free book by Étienne Ghys
CLP: Étienne Ghys has uploaded an entire book to the arXiv! It’s called A Singular Mathematical Promenade and tells a winding tale that starts with one of his colleagues writing down a New Maths Fact on the back of a Paris metro ticket.
Over the course of about 300 pages, Ghys takes us on a tour of a smorgasbord of mathematical concepts, leading up to “the precise description of the chord diagrams that occur in the neighborhood of a singular point of a planar real analytic curve”.
It’s like a mathematical road trip, and it’s beautifully presented. Ghys must be a TeX wizard!
I haven’t had a chance to do any more than skim it so far, but I’m seriously considering printing it out and reading the whole thing – Étienne Ghys is very good at explaining very hard maths.
A Singular Mathematical Promenade on the arXiv
Cheng is still at it
Katie: To round out the year nicely, mathmo-at-large Eugenia Cheng has yet again come up with the perfect formula for something, and this time as a nice festive twist it’s for the perfect mince pie. The formula involves calculating the ratio of pastry to filling; she’s used a nice bit of calculus to optimise the ratio, and worked out a way to improve your pies, regardless of the angle of slope/ratio of base/opening of your mince pie cases, by trimming one of the layers before assembly.
Sadly, the Telegraph seems to think that people would be more interested in watching a horrifically chopped down version of the video that doesn’t make any sense and loses any semblance of interesting. Luckily though, we’ve found the full version.
Bafflingly, this video seems to be a promo for the new maths gallery at the Science Museum. Don’t ask how, we don’t know.
The mathematical formula for the perfect mince pie, at The Telegraph
How to make the perfect mince pie – using maths, at Barcroft TV
Pity gif #15 is only Riemann integration– they could have gotten Lebesgue just as easily!!