Let’s recite the $13$ times table. Pay attention to the first digit of each number:
\begin{array}{l} \color{blue}13, \\ \color{blue}26, \\ \color{blue}39, \\ \color{blue}52 \end{array}
What happened to $\color{blue}4$‽
A while ago I was working through the $13$ times table for some boring reason, and I was in the kind of mood to find it really quite vexing that the first digits don’t go $1,2,3,4$. Furthermore, $400 \div 13 \approx 31$, so it takes a long time before you see a 4 at all, and that seemed really unfair.
I was being pretty unreasonable in my expectations of basic arithmetic, but I wasn’t completely brain-dead: I smelled an integer sequence! How about
$a(n)$ = least $k$ such that $k \times n$ starts with a $4$.
That’s not particularly interesting, and someone who comes across this sequence in the OEIS might think “why $4$?” So, I did a bit more thinking and came up with this:
$a(n)$ = least $k$ such that $\{ \text{first digit of } j \times n, \, 0 \leq j \leq k \} = \{ 0,1,2, \dots 9 \}$
I wrote a bit of Python, and in a few minutes I had some numbers:
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $a(n)$ | 9 | 45 | 27 | 23 | 18 | 15 | 13 | 12 | 9 | 9 | 9 | 42 | 62 |
And hey, $13$ is a record-setter. I’m really beginning to dislike this number. Anyway, I searched the OEIS for my sequence and it wasn’t there, so I submitted it and it was duly accepted as A249067.
Along the way, OEIS editor Charles R Greathouse IV added this intriguing conjecture:
Conjecture: $a(n) \leq N$ for all $n$. Perhaps $N$ can be taken as $81$.
Why $81$? Maybe look at the graph produced automatically by the OEIS:
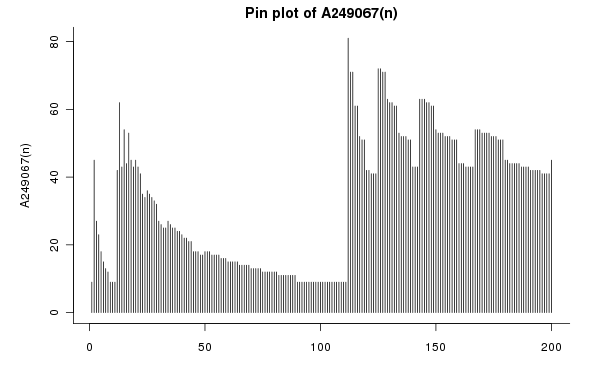 The record of $81$ is reached at $a(112)$. And at $a(1112)$. And $a(11112)$. That’s because they’re very slightly bigger than $\frac{1}{9} \times 10^m$, so nine times $1 \dots 12$ is just bigger than $9 \dots 9$, i.e. a number starting with a $1$, so it takes nine times nine steps down the times table before you see a number with $9$ as its first digit.
The record of $81$ is reached at $a(112)$. And at $a(1112)$. And $a(11112)$. That’s because they’re very slightly bigger than $\frac{1}{9} \times 10^m$, so nine times $1 \dots 12$ is just bigger than $9 \dots 9$, i.e. a number starting with a $1$, so it takes nine times nine steps down the times table before you see a number with $9$ as its first digit.
This pattern repeats at every power of $10$, and in fact every pattern in this sequence repeats (more or less) at every power of 10: this animated plot of the sequence with different horizontal scales shows that it’s self-similar:
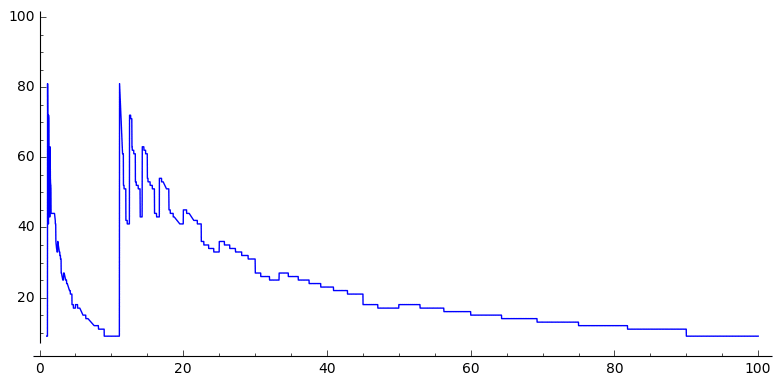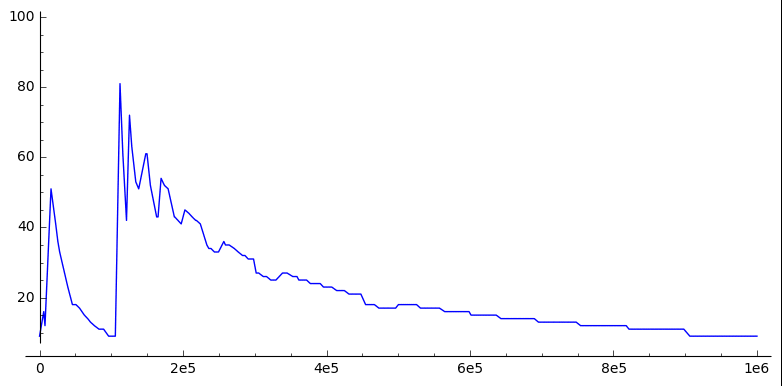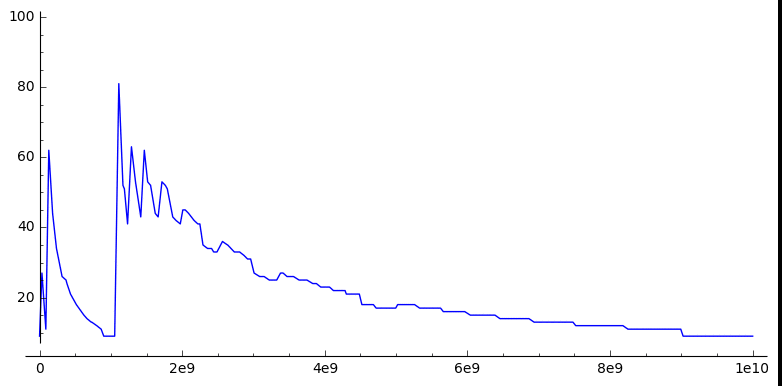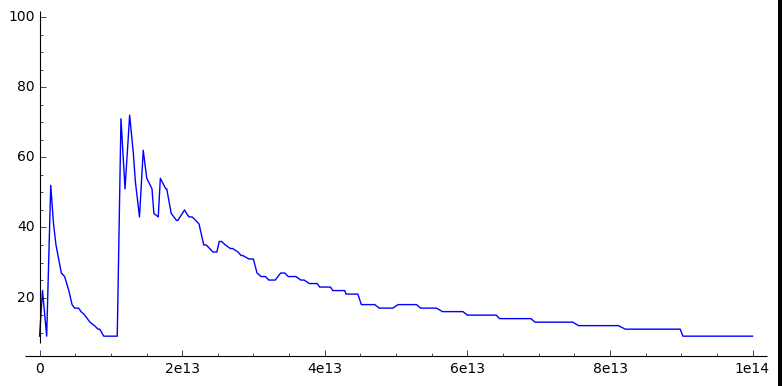
(The fuzziness in the bigger plots is because each plot just takes a sample of points, and interpolates between them)
So the conjecture looks true, and this is my sequence, so I should prove it.
It isn’t surprising that this thing repeats when you multiply by $10$: we’re only looking at the first digit, and obviously the first digit of $n$ is the same as the first digit of $10n$. That doesn’t suffice as a proof of Charles Greathouse’s conjecture though: numbers which don’t end in a $0$ might do something unhelpful.
Fortunately, the day after I thought this sequence up was MathsJam night. I decided I’d set the Charles Grey pub’s brightest minds on the problem. I had a few ideas but I’m not particularly quick at putting thoughts together.
Ji proposed an application of the pigeonhole principle: if you look at the first two digits of the numbers you see in $n$’s times table, you can write out everything you might see in a $9 \times 10$ grid:
\begin{array}{}
10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 \\
20 & 21 & 22 & 23 & 24 & 25 & 26 & 27 & 28 & 29 \\
30 & 31 & 32 & 33 & 34 & 35 & 36 & 37 & 38 & 39 \\
40 & 41 & 42 & 43 & 44 & 45 & 46 & 47 & 48 & 49 \\
50 & 51 & 52 & 53 & 54 & 55 & 56 & 57 & 58 & 59 \\
60 & 61 & 62 & 63 & 64 & 65 & 66 & 67 & 68 & 69 \\
70 & 71 & 72 & 73 & 74 & 75 & 76 & 77 & 78 & 79 \\
80 & 81 & 82 & 83 & 84 & 85 & 86 & 87 & 88 & 89 \\
90 & 91 & 92 & 93 & 94 & 95 & 96 & 97 & 98 & 99
\end{array}
The $n$ times table will dance around this grid until all nine rows have been visited. The longest it can do that is by visiting all 80 cells not in the last line. If the process doesn’t visit the same place twice before it hits every row, that means that the latest you can put off visiting the last row is the 81st iteration. So we need to show that you can’t visit the same spot twice before visiting each row once.
Unfortunately, that’s not true. The $12$ times table visits the ’12’ cell at $12 \times 1 = 12$ and again at $12 \times 10 = 120$, before all possible first digits have been seen.
So, we need another explanation.
Katie Steckles and the Manchester MathsJam crowd came up with an alternate explanation: if you can prove $\left\lceil \frac{1}{9} \cdot 10^m \right\rceil$ (that is, $112$, $1112$, $\ldots$) takes 81 steps for all $m \geq 3$, then that’s the maximum, as any $m$-digit number bigger than that will reach $9 \times 10^m$ in at most as many steps, and will definitely have seen all the other initial digits before then, and any $m$-digit number smaller than $\left\lceil \frac{1}{9} \cdot 10^m \right\rceil$ will visit every first digit in the first 9 multiples.
There’s some evidence for this: the $m+3$-digit numbers that take 81 steps seem to be the ones between $11\ldots112$ and $112499\ldots99$.
I don’t know if there’s a clever way of showing that $\left\lceil \frac{1}{9} \cdot 10^m \right\rceil$ takes 81 steps, but would it convince you if I said that $112$ takes that long, and adding more $1$s in the middle can’t make it any worse? Anyway, that’s good enough for me.
I think I can now answer my question: exactly how bad is the $13$ times table? Let’s compute the record-setters for A24097: the numbers that take longer than any smaller number to see every possible leading digit:
| $n$ | 1 | 2 | 13 | 112 |
|---|---|---|---|---|
| $a(n)$ | 9 | 45 | 62 | 81 |
$13$ is a record-setter in the sequence, which means it’s pretty bad, but it’s not the worst: we’ve shown above that $112$ takes the longest possible number of steps to see every digit. And the number $2$ comes under scrutiny for taking way longer than its neighbours. So really, $13$ is just unlucky to find itself in such company.
If you’re interested in the working-out I did for this post, I’ve put my Jupyter notebook online.
David Cushing had a hunch that the maximum number of steps in base $k$ would be $(k-1)^2$ (so in base $10$, the maximum is $9^2 = 81$). I’ve checked up to base $25$, and that hunch seems to be right.