My wife’s grandmother is a fearsome character. She’s in her nineties but still has all her wits about her. In fact, she’s got more than her fair share of wits. Whenever we visit her, she hits me with a barrage of questions and puzzles collected from the last several decades of TV quiz shows and newspaper games pages. My worth as a grandson-in-law is directly proportional to how many answers I get right.
One of her favourite modes of attack is the “30 Second Challenge” from the Daily Mail. It looks like this:
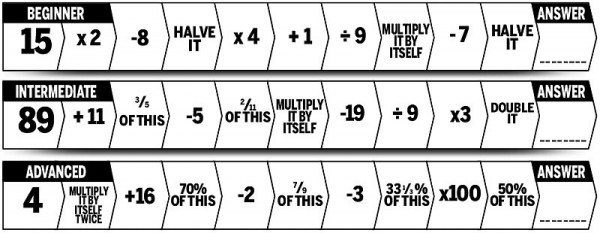
You start with the number on the left, then follow the instructions reading right until you get to the answer at the end. It’s one of Grandma’s favourites because it’s very hard to do in your head when she’s just reading it out!
I decided it would be a fun Sunday morning mental excursion to make a random 30 second challenge generator.