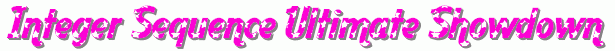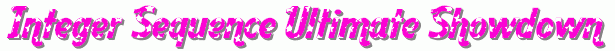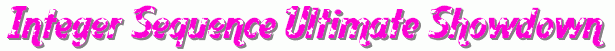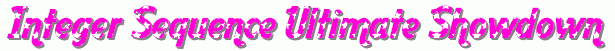CP walks into the office.
Cushing: Christian, look at this. I’ve asked Wolfram Alpha to plot a quadratic going through three squares.
CP walks into the office.
Cushing: Christian, look at this. I’ve asked Wolfram Alpha to plot a quadratic going through three squares.
Well! I have been quite remiss in writing up the Newcastle MathsJams. The last recap published was for May’s meeting. The end of the year (and associated holiday) is a good time to kick myself up the backside and do the entire second half of the year in one go. So, here’s that.
Happy birthday to Turismo Matemático, a happy little blog which has been posting pictures of mathematical objects around the world for five years now. It’s one of my favourite maths blogs; if you weren’t already aware of it, now’s as good a time as any to go and have a look.
A006720
Somos-4 sequence: $a(0)=a(1)=a(2)=a(3)=1$; for $n \geq 4$, $a(n)=(a(n-1)a(n-3)+a(n-2)^2)/a(n-4)$.1, 1, 1, 1, 2, 3, 7, 23, 59, 314, 1529, 8209, 83313, 620297, 7869898, 126742987, 1687054711, 47301104551, 1123424582771, 32606721084786, 1662315215971057, 61958046554226593, 4257998884448335457, 334806306946199122193, ...
The building where I work is named after Alexander Stewart Herschel. I suspect this is because it used to be the home of the physics department, since he was an astronomer, but it works for us too because he also has a pretty cool graph named after him.
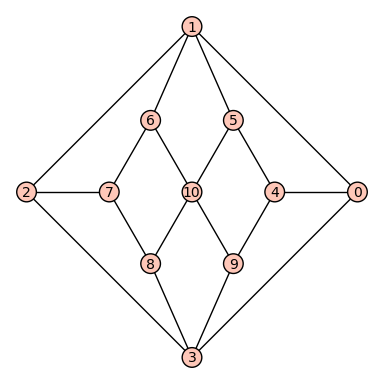
An embedding of the Herschel graph in the plane
Helpfully, it’s called the Herschel graph. It’s the smallest non-Hamiltonian polyhedral graph – you can’t draw a path on it that visits each vertex exactly once, but you can make a polyhedron whose vertices and edges correspond with the graph exactly. It’s also bipartite – you can colour the vertices using two colours so that edges only connect vertices of different colours. The graph’s automorphism group – its symmetries – is $D_6$, the symmetry group of the hexagon. That means that there’s threefold rotational symmetry, as well as a couple of lines of reflection. It’s hard to see the threefold symmetry in the usual diagram of the graph, but it’s there!
Anyway, at the start of the summer, one of the lecturers here, Dr Michael White, told me about this graph and asked if we could work out how to construct the corresponding polyhedron. Making a polyhedron is quite simple – take the diagram on the Wikipedia page, pinch the middle and pull up – but it would be really nice if you could make a polyhedron which has the same symmetries as the graph.
Over on Google+, David Roberts just posted this trailer (via Антид Ото) to a lovely documentary about Julia Robinson and her contributions towards answering Hilbert’s tenth problem.
[youtube url=https://www.youtube.com/watch?v=e4x9XKNAYjU]
David Hilbert’s tenth problem was to find an algorithm to solve diophantine equations, that is, to find roots of polynomials with integer coefficients. We now know that the problem is unsolvable in general, and Julia Robinson did a lot of the work to get there; she wrote that she “couldn’t bear to die without knowing the answer.”
David asked if anyone knows of any present-day female mathematicians of similar standing to Julia Robinson. Apart from President of the IMU Ingrid Daubechies and people who are active on Twitter my knowledge of top mathmos is quite poor, so I thought I’d open the question up to The Aperiodical’s readers.
The full DVD of Julia Robinson and Hilbert’s Tenth Problem is available from George Csicsery’s ZALA Films site, and it looks like there are a few copies on Amazon as well.
Welcome to the Field of Dreams. Talking of which: why can’t you grow wheat in $\mathbb{Z}/6\mathbb{Z}$?
Anyway, we’re finally here: the Grand Finale of our tournament to find the Integest Sequence 2013. Here’s a reminder of the sequences vying for the title:
It’s a been a long, hard battle. We’ve seen some good sequences, some bad sequences, and an awful lot of plagiarised GIFs. So, without further ado, it’s time to start the