Here’s some mathematical news that didn’t make it on to the site otherwise this month.
Maths News
There’s been more abc conjecture drama: Peter Scholze and Jakob Stix are in line for a ¥140m (around £766k) prize for their paper pointing out the flaw in Mochizuki’s claimed abc proof – if they publish it in a journal.
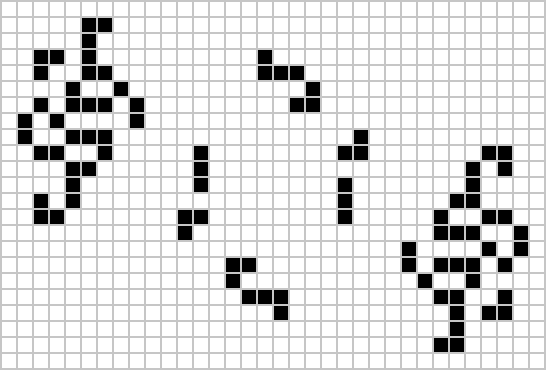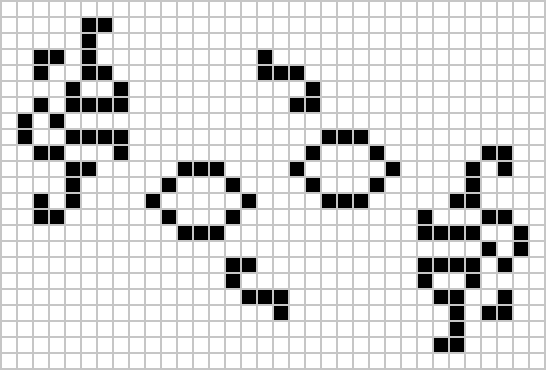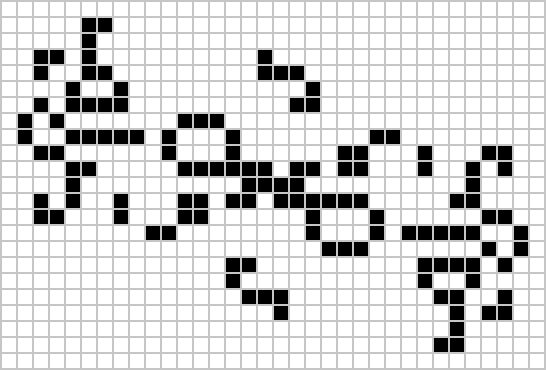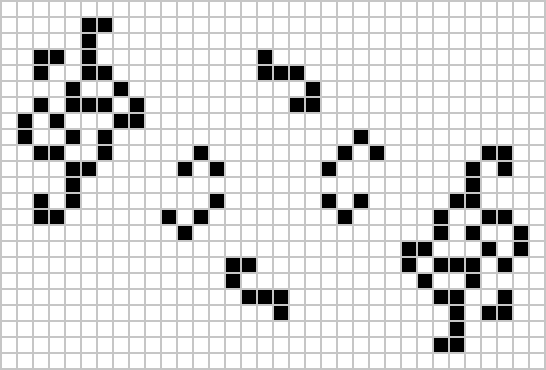
A period 19 oscillator has been found in Conway’s game of life – the discussion thread on ConwayLife just gives it as a series of coordinates, but it already has an entry on LifeWiki, where it’s called ‘Cribbage’. (via Isaac Grosof)
Then, a week later, the first ever period 41 oscillator was also found! Excitingly named 204P41 (consisting of 204 cells) it’s led to another discovery – it looks like we now know how to make oscillators with any period, meaning Game of Life is omniperiodic. Since 2013 we’ve known all periods above 43 were possible, and this fills a gap in this excellent table.
Lean’s mathlib has been completely ported to Lean4 – if you’re familiar with proof assistants, you may find this news exciting or significant. Here’s a video showing off what that looks like. Meanwhile, the Lean Focused Research Organization has been set up to “advance the formal mathematics revolution”. (via @leanprover@functional.cafe)
Events and Organisations
Inclusion/Exclusion, a justice and maths blog, has posted an open letter to the MAA about holding MathFest in Florida, requesting an option for online participation due to the state’s recent draconian law changes. It pulls ε punches:
Regardless of any in-person safeguards that MAA may put in place, this year’s MathFest will not be a safe event for trans people, for undocumented immigrants, or for many other members of our community, including disabled people. Therefore, our most urgent request is that you provide an online participation option.
Excerpt from the open letter
If π approximation day on 22/7 got you thinking about your plans for the next actual π day, you might find it useful to know that the International Day of Mathematics 2024 theme is Playing With Math. From their website, “In 2024 we want to celebrate mathematical games, puzzles and other entertaining activities, but also “playing” with mathematics itself, exploring, experimenting, and discovering.”
Speaking of mathematical games, Ben Orlin has released a book of solitaire games as a follow-up to his “Math Games with Bad Drawings”. It’s available for free on his website as a PDF, and therefore weighs infinity less than the actual book it’s a follow-up to, which is so huge it’s collapsed into a black hole under its own mass. (via Patrick Honner)
And finally: Tim Wall, the Australian group theorist, has died. According to his profile on the Australian Academy of Science website, Wall “has made highly significant and original contributions to the development of Algebra, in particular to the Theory of Groups. […] He has always instinctingly given of his ideas to his collaborators and younger colleagues.” Thanks Tim!