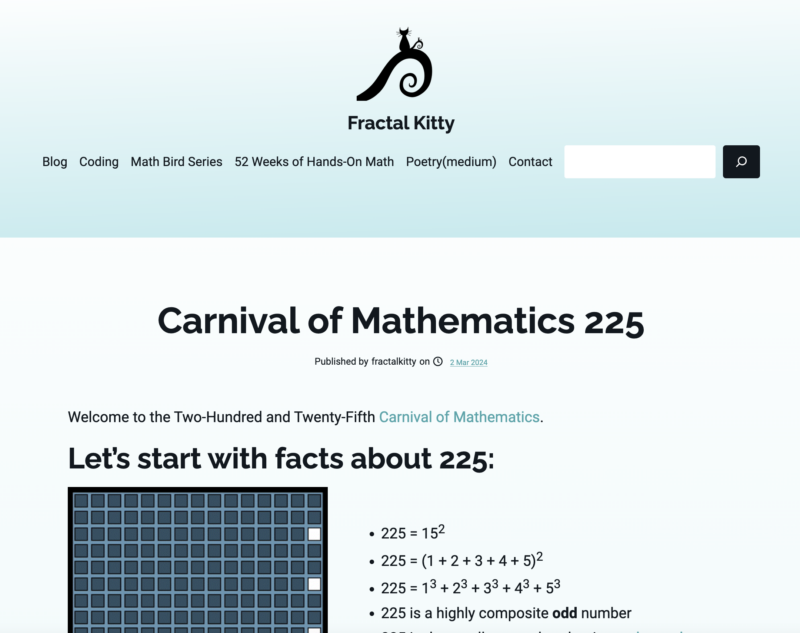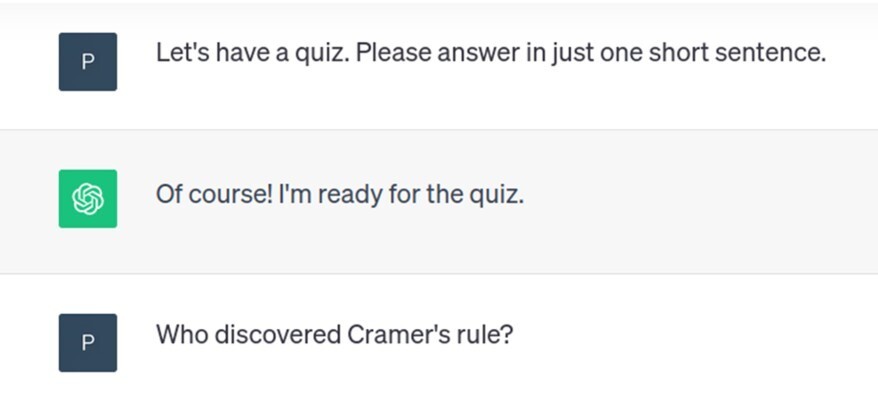
You know how loads of things in maths are named for the wrong person? In 1996, a fun quiz appeared in The Mathematical Gazette based on history of maths misconceptions. It contained a series of questions where the obvious answer is not correct, such as “Who discovered Cramer’s rule?”, “Did Pascal discover the Pascal triangle?”…