In this series of posts, we’ll be featuring mathematical video and streaming channels from all over the internet, by speaking to the creators of the channel and asking them about what they do. We spoke to Keenan Crane, a professor in Computer Science & Robotics at Carnegie Mellon University, who runs his own YouTube channel…
Aperiodical News Roundup – October 2023
Here’s a round-up of a few things that happened this month that we didn’t otherwise cover here. The Salem Prize for 2023, given annually to young mathematicians judged to have done outstanding work on harmonic analysis and related topics, has been awarded to Sarah Peluse and Julian Sahasrabudhe. (via Terence Tao) According to this recent…
Carnival of Mathematics 221
The next issue of the Carnival of Mathematics, rounding up blog posts from the month of October 2023, is now online at Beauty of Mathematics. The Carnival rounds up maths blog posts from all over the internet, including some from our own Aperiodical. See our Carnival of Mathematics page for more information.
\(-e^{i\pi}\) to Watch: Kat Does Maths
In this series of posts, we’ll be featuring mathematical video and streaming channels from all over the internet, by speaking to the creators of the channel and asking them about what they do. We spoke to Kat Phillips, who’s been running regular mathematical livestreams on Twitch through her channel KatDoesMaths since 2020, and has over…
Finite Group: first free live stream

As we wrote about recently, we (Katie and Peter, along with our friends Sophie Maclean and Matthew Scroggs) are involved in an exciting new initiative – an online maths community that gets together via online chat and monthly video events. The first event happened yesterday evening, and will be available to watch for free on…
\(-e^{i\pi}\) to Watch: Tibees
In this series of posts, we’ll be featuring mathematical video and streaming channels from all over the internet, by speaking to the creators of the channel and asking them about what they do. We spoke to Toby Hendy, author of the YouTube channel Tibees, which has over a million subscribers.
2. Four bugs
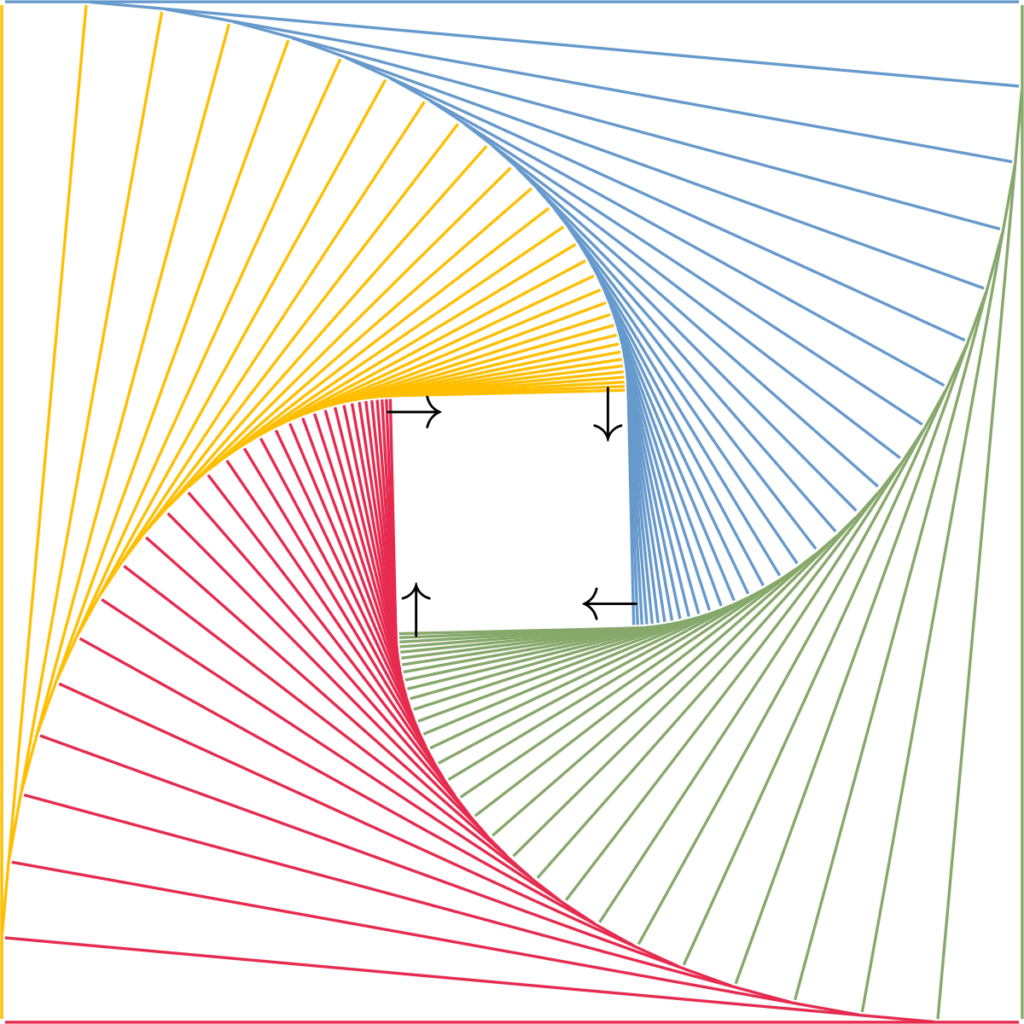
Reminder: I’m occasionally working to (sort of) recreate Martin Gardner’s cover images from Scientific American, the so-called Gardner’s Dozen. This time I’m looking at the cover image from the July 1965 issue, accompanying the column on ‘op art’ (which became chapter 24 in Martin Gardner’s Sixth Book of Mathematical Diversions from Scientific American).