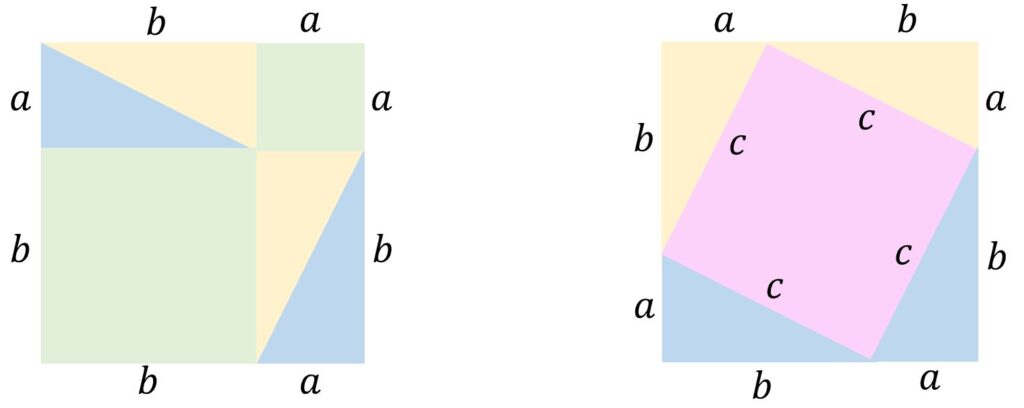
In this guest post, David Benjamin shares a cornucopia of concepts and stories relating to Pythagoras and his famous theorem. I admit to mild irritation when I’m told that Pythagoras’ theorem is $a^2+b^2=c^2$. The theorem is based on area – in particular, that of squares. There are many proofs of the theorem and in this…





