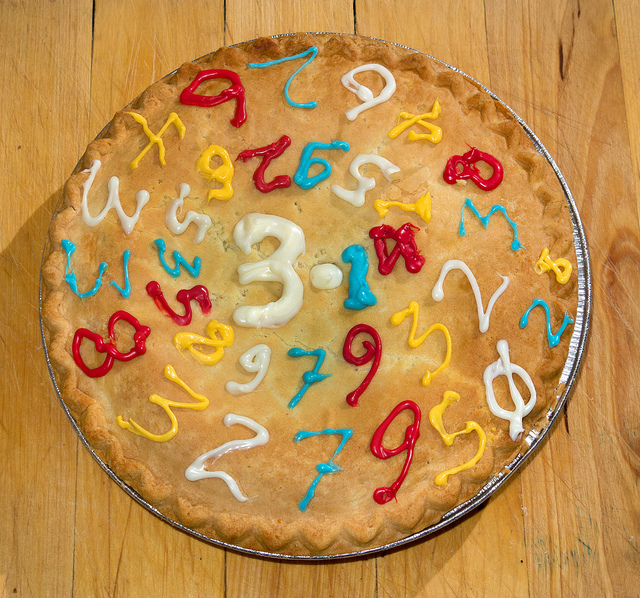‘Tis the season to celebrate the circle constant! ((Pedants would have me revise that to “a circle constant”.)) Yes, that’s right: in some calendar systems using some date notation, the day and month coincide with the first three digits of π, and mathematicians all over the world are celebrating with thematic baked goods and the wearing of irrational t-shirts.
And the internet’s maths cohort isn’t far behind. Here’s a round-up (geddit – round?!) of some of our favourites. In case you were wondering, we at The Aperiodical hadn’t forgotten about π day – we’re just saving ourselves for next year, when we’ll celebrate the magnificent “3.14.15”, which will for once be more accurate to the value of π than π approximation day on 22/7. (Admittedly, for the last few years, 3.14.14 and so on have strictly been closer to π than 22/7. But this will be the first time you can include the year and feel like you’re doing it right.)

 Welcome to the 145th Carnival of Mathematics, hosted here at The Aperiodical.
Welcome to the 145th Carnival of Mathematics, hosted here at The Aperiodical.