Here’s a bar bet you can’t lose. Actually, it’s more of a kitchen bet, being a quiche cutting conundrum.
You’ve just bought a lovely fresh haggis quiche at your local Minus 4 shop and are planning to eat it in one sitting, in your kitchen with a friend. You’ve agreed to share it in the fairest possible way: one of you cuts and the other choses. The quiche is in the usual circular shape.

A coin is tossed—rather unnecessarily, it must be said—and it is determined that your friend gets to cut. You step out of the kitchen for a moment and upon your return discover to your horror that your friend has already done the cutting, but not as you had expected. Instead of making one simple straight cut as close to a diameter as possible, the big oaf has made four straight cuts.

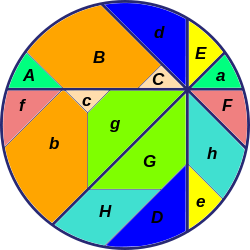
Despite the fact that these four cuts neatly meet at 45 degrees at a single point, everything is off-centre. The first cut is close to being a diamater, but the others are more lop-sided. The resulting eight slices are unequal in size, and the near-diameter cut clearly doesn’t bisect the quiche either.
“What have you done, Hamish?” you cry out in exasperation. “You were only supposed to make one cut, then I’d get to chose which piece I wanted. I was assuming you’d be smart enough to cut it into two pieces which looked so similar you wouldn’t mind which one I took for myself. That was the whole point! But now, even if we pretend you only made one of those four cuts, they’re all so skewed that it won’t seem fair, as it would be too easy for me to get four adjacent pieces that add up to more than half the quiche.”
“Sorry,” he replies sheepishly. “I thought that just two pieces would be too big. So I went for eight smaller ones. Besides, this is how I always cut deep-fried Mars bars.”
Trying to suppress the look of disbelief that has come over your face, you force Hamish to sit down for five minutes and read the Wikipedia page on fair cake-cutting.
“Now do you get it?” you ask. “With two pieces it’s easy, but with eight pieces it’s much trickier!”
“To be honest, I got lost early on reading that webpage,” Hamish confesses. Glancing over his shoulder you can see why, as the easy two-piece case is buried deep in the article.
“I’ll try to make it up to you,” Hamish offers. “Why don’t I divide these eight pieces into two piles of four, as fairly as I can, and you get to pick whichever pile you like?”
“Hmm, I guess that would work,” you reply. Then a revelation hits you. “Actually I have a better idea. Please let me do the division into two piles of four pieces, and you can chose whichever pile you want. Furthermore, I’ll do this with my eyes closed. You can even rotate the plate first so I don’t even know which piece is where. And I’ll bet you a tenner that I’ll do such a good job that no matter which pile you chose you won’t get much more than me! You can verify using the kitchen scales over there. You can even change your mind after you choose and weigh. You can’t ask for more than that!
It’s Hamish’s turn to be incredulous. He can’t believe his luck, being convinced that he’ll soon be £10 richer, since he doesn’t think you’ll be able to pull it off as you claim.
You close your eyes as promised, having first placed two identical clean plates on the table, one to the left of the quiche, the other to the right. Hamish spins the plate in front of you and says, “Ready? You can touch but don’t look.” You reach forward and quickly remove four pieces of the quiche and set them on the plate on the left. You open your eyes and put the remaining four on the plate on the right. Hamish picks one plate for himself, and then weighs both of them. To his astonishment he finds that he has lost the bet fair and square, even if he switches plates at this late stage. Crestfallen, he hands over ten quid.
What is it you do that guarantees your success here? This picture reveals all.
Even though your eyes are closed, it’s easy to remove four alternate slices to the plate on the left. If the four slices left behind are placed on a similar plate, and the two are weighed, they should come out more or less equal.
This works because of the little known and oft-misnamed Quiche Theorem, which asserts:
If a circular quiche is divided into 4n slices (where n is at least 2), by making cuts at equal angles through an arbitrary internal point, then the sums of the areas of alternate slices are equal.
Okay, so that’s really a 2D result about area, but we’ve just added depth (and flavour) to it.
This applies when we have 8, 12, or 16 slices, but not if there are 4, 6, 10 or 14. Furthermore, since the crust on a quiche can be viewed as the difference between the whole quiche and a slightly smaller circle of filling, with the same centre, and each circle behaves according to the theorem, it follows that you and Hamish also get equal amounts of crust.
Curiously, in cases where the number of slices isn’t a multiple of 4, the alternate slice strategy gives one person more quiche but less crust, and vice versa.
For 8 slices, Carter & Wagon (1994) gave a disection proof of the alternating slice strategy.
Maybe you should let Hamish loose with the knife a little longer, then he could see for himself, without resorting to weighing, that the quiche can be split into two equal-weight halves consistent with his initial 4 cuts. He’d then have sixteen mostly bite-sized pieces, half of which would match up with the other half, down to the last crust.
THE END
If you need to see the theorem in action, here’s a reproduction of Carter and Wagon’s proof without words in a GeoGebra worksheet. Drag the big blue points around to change the slices.
Very interesting. I work in Mathematics Museum at Mexico with children. any site or pdf with card tricks?
Thanks a lot
This result is usually called the “Pizza Theorem”. There is also
an associated “Crust Theorem”. See the Tipping Point Math
video https://www.youtube.com/watch?v=UXRUiTEZgbA