Welcome to the seventh match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

Ian Stephenson – Why your projects are always late…

Ian blogs about programming at www.sniff.org.uk.

Every big project ends up running over time, and going over budget. No matter how carefully you plan, the real thing takes longer than you thought it would. It turns out the reason for that is you’ve been doing the maths incorrectly.

Project planning usually starts by breaking the job into smaller tasks and estimating how long they’ll take. Then those get lined up, taking into account dependencies to find the critical path, and that’s how long the job takes. Then we probably add a little slack in just in case something goes wrong…

Estimating how long each task will take is the hard part here – especially when we’re being asked to develop something new, so let’s make it a bit easier, and pick a task you know how to do well, and you’ve done many times before:

How long will it take you to drive from home to work?

Easy you say… it takes 20 mins.

Great, so we allocate 20 mins in the schedule. We might have a bunch of other tasks which we’re equally confident about, and we put them all into MS Project, let it do its thing, and by the end of the project we struggle to hit the deadline, because even for simple tasks like this the estimates are bad. Let’s look at that estimate more closely… 20 mins you say? Sure 9 times out of 10 it takes 20 mins. So what’s the chances of you getting there in 15 mins? Well it’s possible if there was no traffic, and you hit every light, but its an absolute best case scenario. 10 mins? Not without breaking the law. What about 25 mins? Sure a bit of traffic… 30 mins? Road works. An hour? There was this one time there was a crash and the road was closed! 3 weeks? I guess if there was some kind of international medical emergency and we were all confined to our homes!

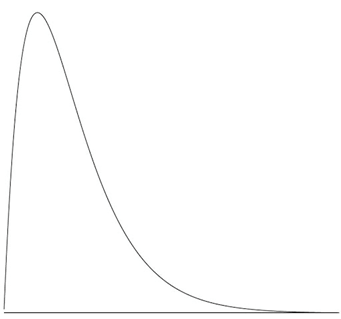
So our graph of probabilities looks something like this. The peak represents 20 minutes. On a good day we can do slightly better, but only slightly. On a bad day, we can do a LOT worse. Now look at the area… Most of the area under the graph is to the right of the 20 minute peak. Most of the time you’re behind schedule.

When asked for your time estimate you gave me the MODE – the most likely time, not the MEAN, the average time.

When you actually perform your task in with the other 10, 20, or 100 others that make up the big project, some of them come in a little ahead of schedule, and some come in a little behind, and some come in a LOT behind. They’re going to combine to produce an expected completion time based on the sum of the means, rather than the sum of the modes, but our estimates are based on the modes. And that’s why your projects are always late.

Sam Hartburn – Phi (Where’d You Come From?)

Sam Hartburn has been addicted to writing mathematical lyrics to well-known songs since 2016.

Phi, or $\phi$, is an irrational number commonly known as the golden ratio. It is equal to $\frac{1+\sqrt{5}}{2}=1.61803\dots$. This is the story of when phi turned up unexpectedly while I was playing with pentagons one evening. It can be sung to the tune of What’s Up by 4 Non Blondes. There’s a karaoke version if you want to sing along.

20 past 10 and I’m having fun
Messing around with a pentagon, to make
A dodecahedron

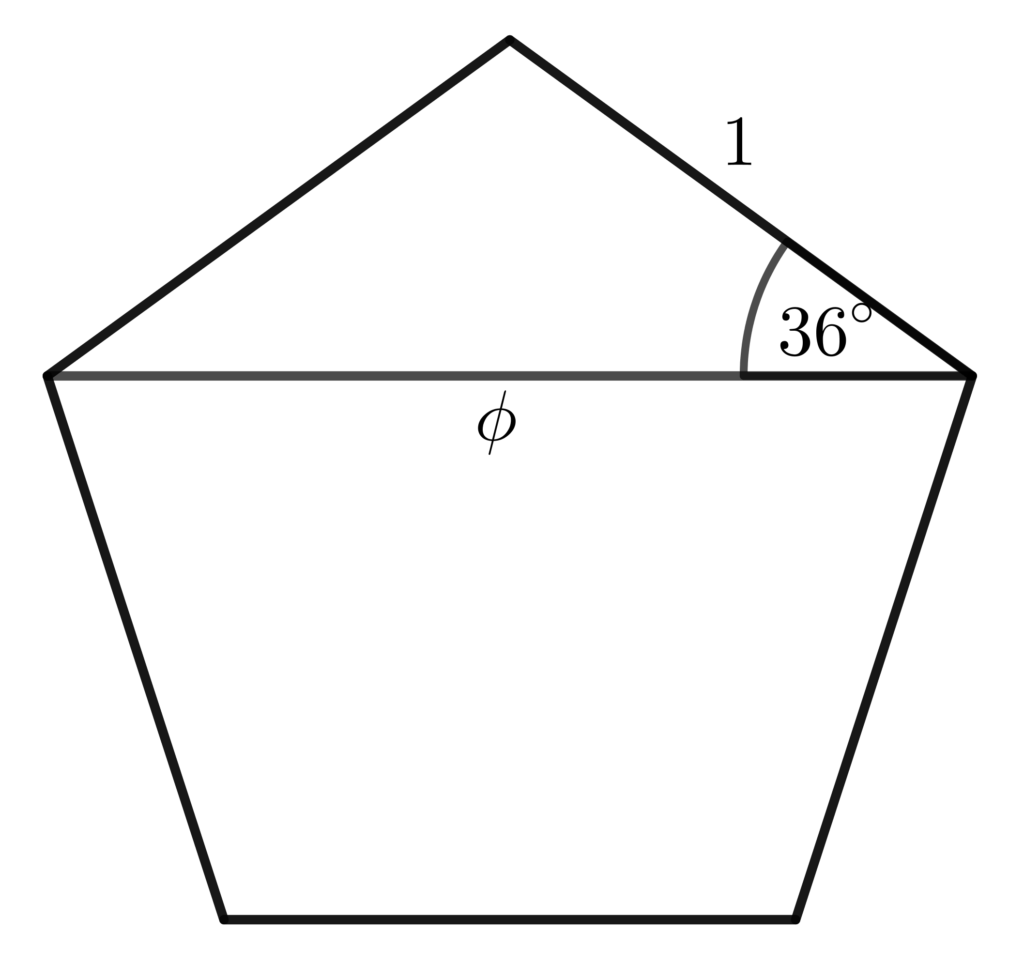
I realise quickly that to make it cool
I need to find out the diagonal, given
That the edge length is 1

And so I draw a line from the left to the right
And I know the angles, I know one side
And I notice something a little peculiar

Because I take 36 and I find the cosine
And I times it by 2 and I see it’s phi
And I scream from the top of my lungs
“Where’d you come from?”

And I say “Phi-i-i-i-i
Phi-i-i”
I said “Phi
Where’d you come from?”

And I say “Phi-i-i-i-i
Phi-i-i”
I said “Phi
Where’d you come from?”

And I try
All night long do I try
I look all the time
For a neat solution

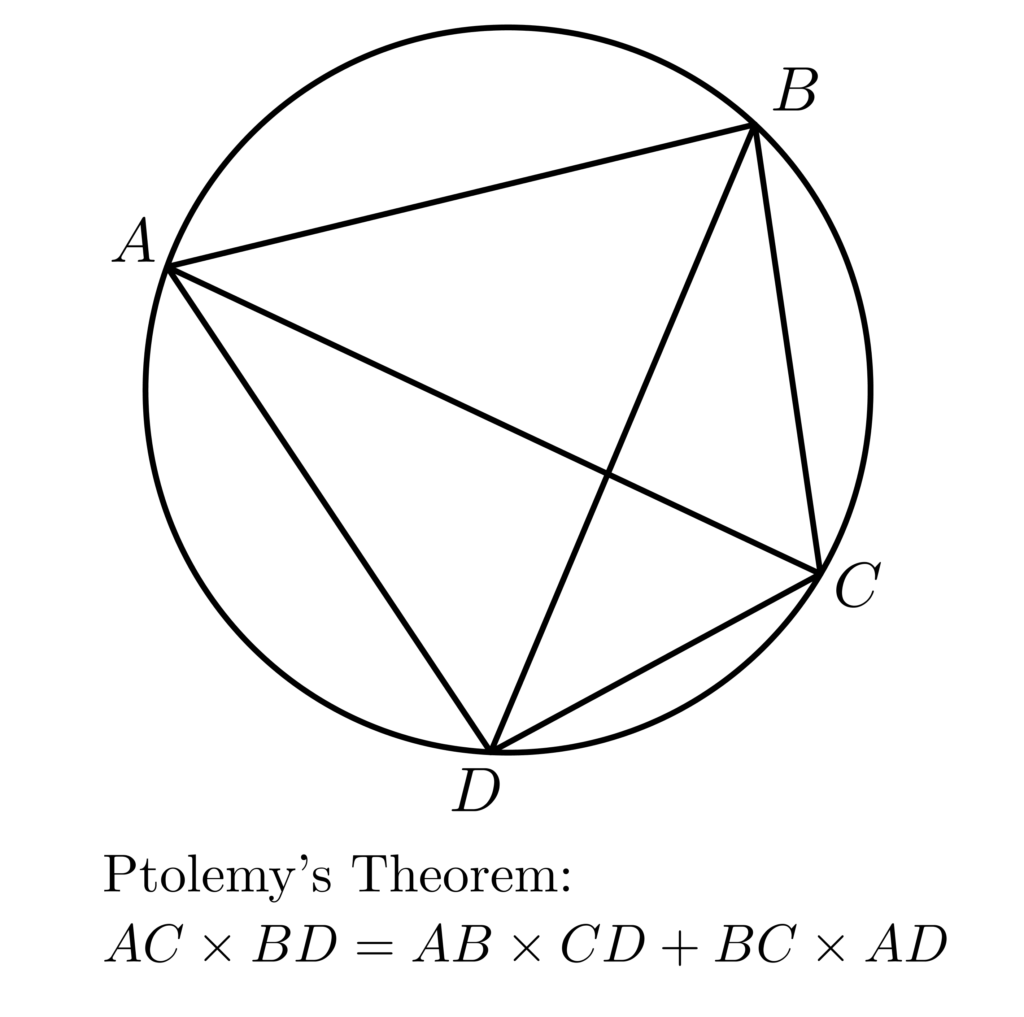
And I see
Oh my word, do I see
A theorem by Ptolemy
It’s a revelation

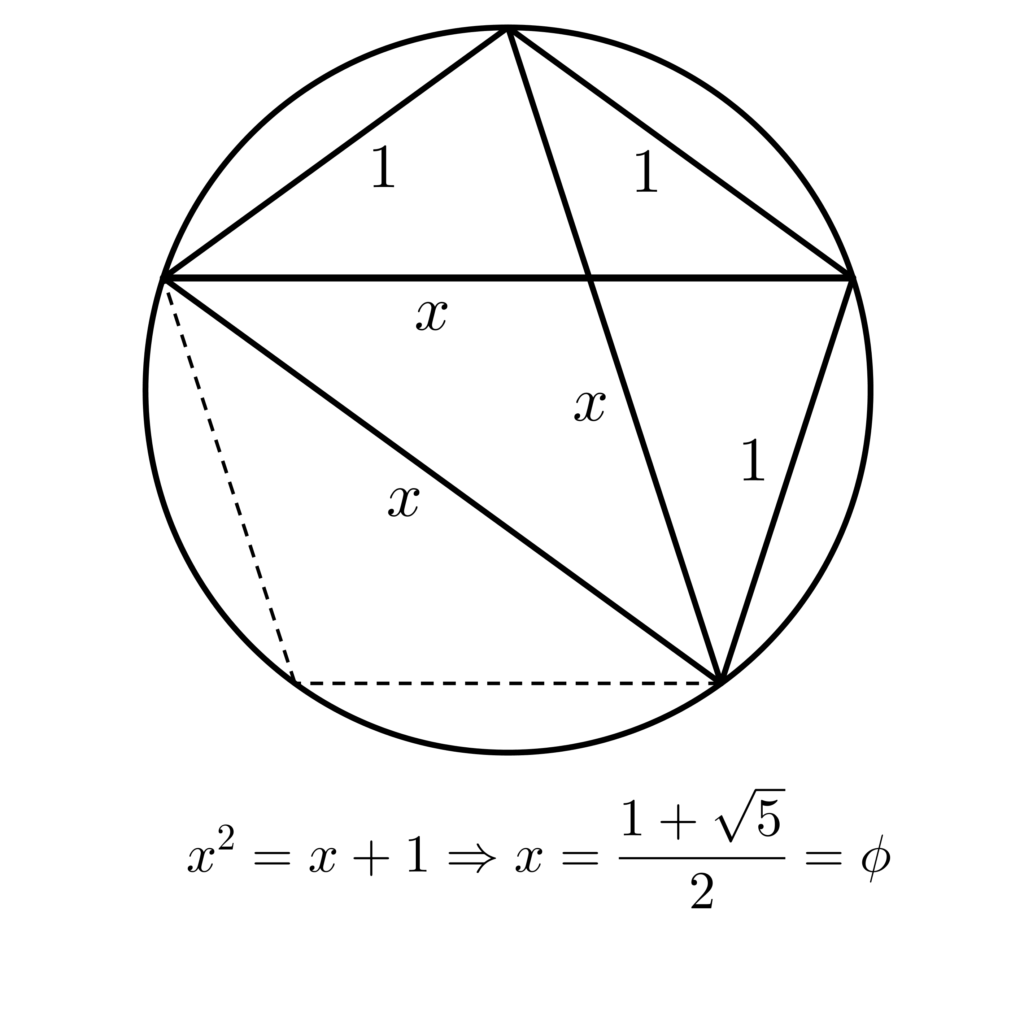
And so I put all the corners on a circle
And I join them all up with diagonals
And I start applying that theorem of Ptolemy

If the diagonal’s $x$ and the side length is 1
Then it gives me $x$-squared equals $x$ plus 1
And I scream from the top of my lungs
“That’s where you’re from!”

And I say “Phi-i-i-i-i
Phi-i-i”
I said “Phi
That’s where you’re from!”

And I say “Phi-i-i-i-i
Phi-i-i”
I said “Phi
That’s where you’re from!”

20 past 2 and although it’s late
I’m happy I stayed up to calculate with phi
And find out where it came from

Zvezdelina Stankova’s Numberphile video has a nice explanation of the concepts in the song. I’m sure there are other good explanations for why phi appears in the diagonal of a pentagon. What others can you find?

Hat tips to Colin Beveridge and Tom Button for discussion about why phi showed up here.

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Saturday the 25th, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.