This is a guest post by David Benjamin.
Rational numbers, when written in decimal, either have a terminating string of digits, like $\frac{3}{8}=0.375$, or produce an infinite repeating string: one well-known example is $\frac{1}{7}=0.142857142857142857…$, and for a full list of reciprocals and their decimal strings, the Aperiodical’s own Christian Lawson-Perfect has built a website which generates a full list.
I’ve collected some interesting observations about the patterns generated by the cycles of recurring decimals, and in particular several relating to $\frac{1}{7}$.
Maximum recurring cycles and the number patterns they generate
For anyone interested, there’s a surprising connection between reptend primes and Fermat primes.
The recurring cycle for $\frac{1}{7}$, which is $142857$, has a length of $6$ digits – and when the length of the cycle produced from a fraction is one less than the denominator of the fraction, the cycle is a maximum recurring cycle. When the denominator is a prime number $>5$, the rational number will always produce a recurring cycle, and many primes produce a maximum cycle. Such primes are called reptend primes and the first fourteen are $7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167$ (OEIS A001913).
The decimal expansion of general fractions of the form $\frac{n}{7}$ also have the interesting property that it contains the same digits in the same cyclic pattern for any value of $n$ up to $6$, but with the start digit shifted along each time: $\frac{2}{7} = 0.285714285714285714…$, $\frac{3}{7} = 0.428571428571428571…$ and so on.
This is not unrelated to the fact that $142857$ is the first cyclic number, and the only one not beginning with zero. Cyclic numbers (OEIS A180340) are so named because when a cyclic number $n$ is multiplied by the numbers from $2$ to $n-1$, it contains the same digits in a different order.
$142857 × 2 = 285714$
$142857 × 4 = 571428$
$142857 × 5 = 714285$
$142857 × 6 = 857142$
If we multiply by multiples of $7$, an interesting pattern appears, which when an addition is applied, shows a further connection:
$142857 × 7 = 999999$
$142857 × 14 = 1999998 \rightarrow 1 + 999998 = 999999$
$142857 × 21 = 2999997 \rightarrow 2 + 999997 = 999999$
$142857 × 392 = 55999944 \rightarrow 55 + 999944 = 999999$, where $392$ is $56 × 7$
Multiplication by any number greater than $7$ but not a multiple of $7$ can also be seen to produce, via an addition, more cycles of $142857$:
$142857 × 9 = 1285713 \rightarrow 1 + 285713 = 285714$
$142857 × 37 = 5285709 \rightarrow 5 + 285709 = 285714$
$142857 × 127 = 18142839 \rightarrow 18 + 142839 = 142857$
$142857 × 3123 = 446142411 \rightarrow 446 + 142411 = 142857$
$142857$ is also a Kaprekar number (OEIS A006886) – when squared, the two halves of the number sum to the original number. Examples include $45^{2}=2025$ for which $20+25=45$, and $297^{2}=88209$ for which $88+209=297$. For our cyclic number, $142857^{2}=20408122449$ and $20408+122449 = 142857$.
Dattatreya Ramachandra Kaprekar (1905-1986) was an Indian mathematician who said of himself, “a drunkard wants to go on drinking wine to remain in that pleasurable state. The same is the case with me in so far as numbers are concerned”.
Adding subsets of digits of cyclic numbers can also be seen to create interesting patterns:
\[14+28+57=99 \qquad 142+857=999 \qquad 1428+5714+2857=9999 \]
We can play the same trick with the second cyclic number $0588235294117647$: $94117647+05882352=99999999$; and using the third cyclic number $052631578947368421$ we have $947368421+052631578=999999999$.
We can also play with squares of subsets of the digits of cyclic numbers:
\[857^{2}-142^{2}=714285 \qquad 94117647^{2} – 5882352^{2}=8823529411764705 \]
For other prime denominators, we don’t always get cyclic patterns like this. The denominator $3$ gives two different cycles, $33333…$ and $66666…$ as does the denominator $13$ ($0769230769230769…$ and $1538461538461538…$). The denominator $11$ yields five different cycles. (For more, read Conway and Guy’s The Book of Numbers).
There is an extraordinary outcome for the set of proper fractions with prime denominator $19$. The maximum recurring cycle for $\frac{1}{19},\frac{2}{19},\frac{3}{19},…..\frac{18}{19}$, when laid out in tabular form, produces a magic square: its rows, columns and leading diagonals have the total $81$.
| 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 |
| 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 |
| 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 |
| 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 |
| 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 |
| 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 |
| 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 |
| 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 |
| 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 |
| 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 |
| 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 |
| 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 |
| 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 |
| 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 |
| 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 |
| 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 |
| 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 |
| 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 |
The first row of the table is the recurring cycle for the rational $\frac{1}{19}$, and the second row is the cycle for the rational $\frac{2}{19}$. The digits for each subsequent row continue in a similar way leading to the final row, the cycle for the rational $\frac{18}{19}$.
Cycles by addition
Another nice pattern here is the remarkable fact that the cycle $052631578947368421$, the recurring section from $\frac{1}{19}$, can be generated from the the powers of $2$. Writing the powers of two in subsequent rows, starting on the right, and then adding the columns gives:
| 1 | |||||||||||||||||||||||||
| 2 | |||||||||||||||||||||||||
| 4 | |||||||||||||||||||||||||
| 8 | |||||||||||||||||||||||||
| 1 | 6 | ||||||||||||||||||||||||
| 3 | 2 | ||||||||||||||||||||||||
| 6 | 4 | ||||||||||||||||||||||||
| 1 | 2 | 8 | |||||||||||||||||||||||
| 2 | 5 | 6 | |||||||||||||||||||||||
| 5 | 1 | 2 | |||||||||||||||||||||||
| 1 | 0 | 2 | 4 | ||||||||||||||||||||||
| 2 | 0 | 4 | 8 | ||||||||||||||||||||||
| 4 | 0 | 9 | 6 | ||||||||||||||||||||||
| 8 | 1 | 9 | 2 | ||||||||||||||||||||||
| 1 | 6 | 3 | 8 | 4 | |||||||||||||||||||||
| 3 | 2 | 7 | 6 | 8 | |||||||||||||||||||||
| 6 | 5 | 5 | 3 | 6 | |||||||||||||||||||||
| 1 | 3 | 1 | 0 | 7 | 2 | ||||||||||||||||||||
| 2 | 6 | 2 | 1 | 4 | 4 | ||||||||||||||||||||
| 5 | 2 | 4 | 2 | 8 | 8 | ||||||||||||||||||||
| . | . | . | . | . | 6 | ||||||||||||||||||||
| . | . | . | . | . | . | 2 | 1 | 0 | 5 | 2 | 6 | 3 | 1 | 5 | 7 | 8 | 9 | 4 | 7 | 3 | 6 | 8 | 4 | 2 | 1 |
$142857$, the recurring cycle for $\frac{1}{7}$, similarly occurs in this sequence of infinite additions. It begins with $7$ at the top, and each subsequent row is obtained by multiplying by $5$ and moving the end of the number to the left one each time. The cycle $142857$ is produced by adding the columns generated.
| 7 | ||||||||||||||||||||
| 3 | 5 | |||||||||||||||||||
| 1 | 7 | 5 | ||||||||||||||||||
| 8 | 7 | 5 | ||||||||||||||||||
| 4 | 3 | 7 | 5 | |||||||||||||||||
| 2 | 1 | 8 | 7 | 5 | ||||||||||||||||
| 1 | 0 | 9 | 3 | 7 | 5 | |||||||||||||||
| 5 | 4 | 6 | 8 | 7 | 5 | |||||||||||||||
| 2 | 7 | 3 | 4 | 3 | 7 | 5 | ||||||||||||||
| 1 | 3 | 6 | 7 | 1 | 8 | 7 | 5 | |||||||||||||
| 6 | 8 | 3 | 5 | 9 | 3 | 7 | 5 | |||||||||||||
| 3 | 4 | 1 | 7 | 9 | 6 | 8 | 7 | 5 | ||||||||||||
| . | 0 | 8 | 9 | 8 | 4 | 3 | 7 | 5 | ||||||||||||
| . | 4 | 9 | 2 | 1 | 8 | 7 | 5 | |||||||||||||
| . | . | . | . | . | . | . | 7 | 1 | 4 | 2 | 8 | 5 | 7 | 1 | 4 | 2 | 8 | 5 | 7 |
The $\frac{1}{7}$ Cycle and Conic Sections
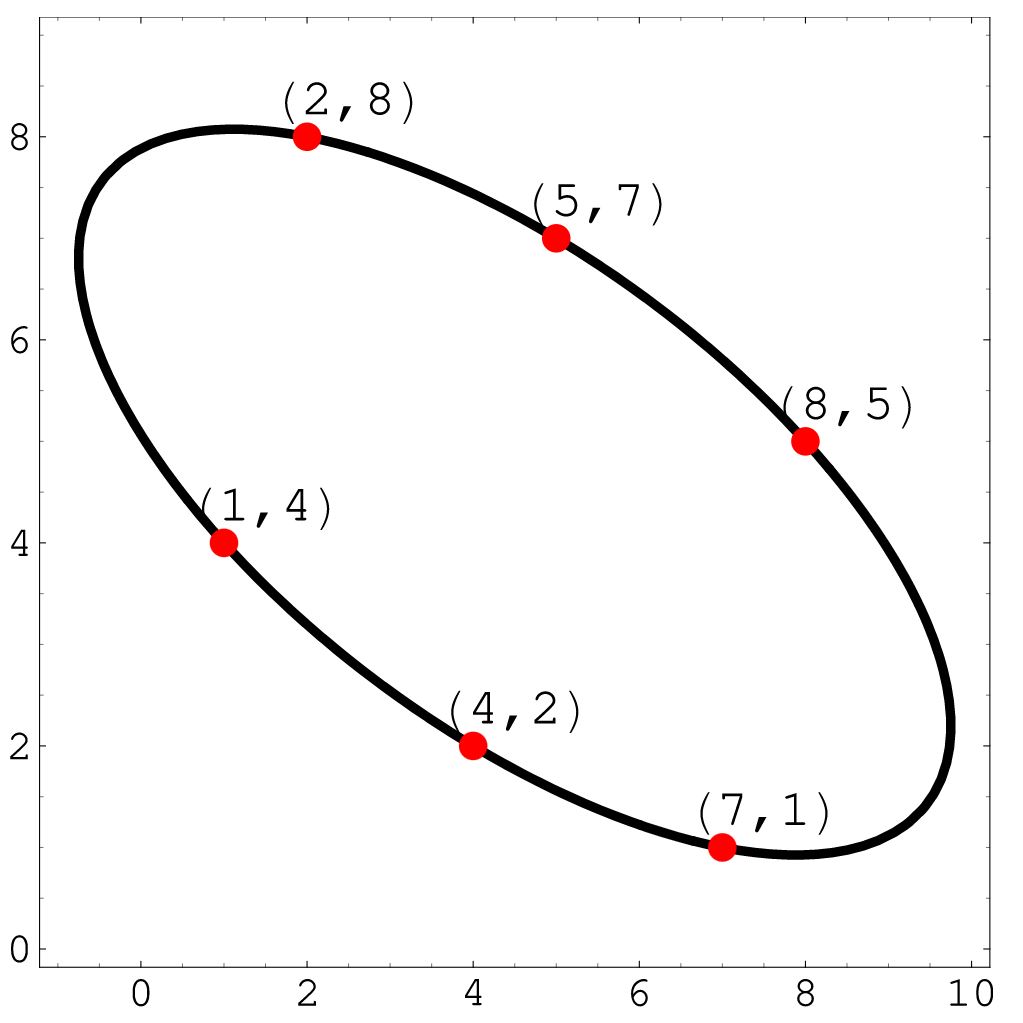
I was surprised to discover in David Wells’ excellent Penguin Dictionary of Curious and Interesting Numbers that the points (1,4) (4,2) (2,8) (8,5) (5,7) and (7,1), formed by overlapping pairs of the digits in the $\frac{1}{7}$ cycle, lie on an ellipse, called the one-seventh ellipse:
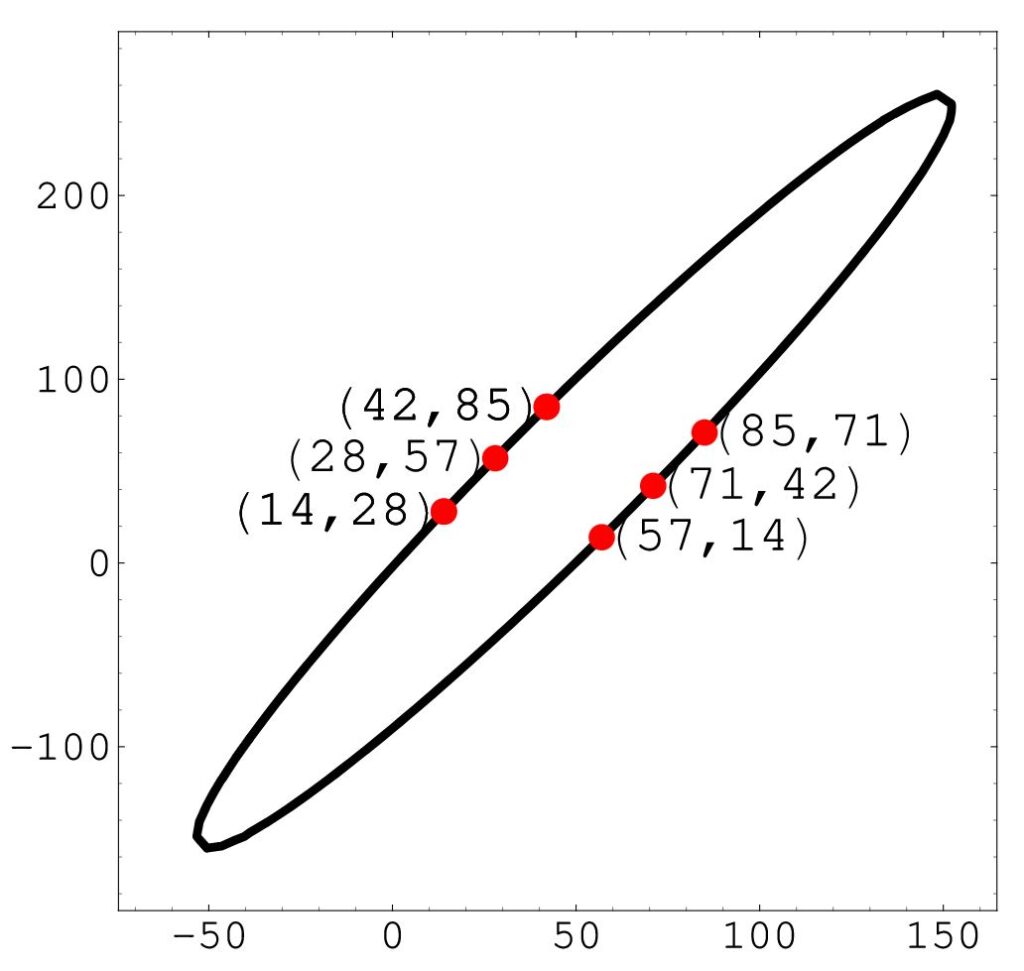
Better still, we can concatenate pairs of digits from the cycle. The points created, (14, 28), (42, 85), (28, 57), (85, 71), (57, 14) and (71, 42), also lie on an ellipse, shown below:
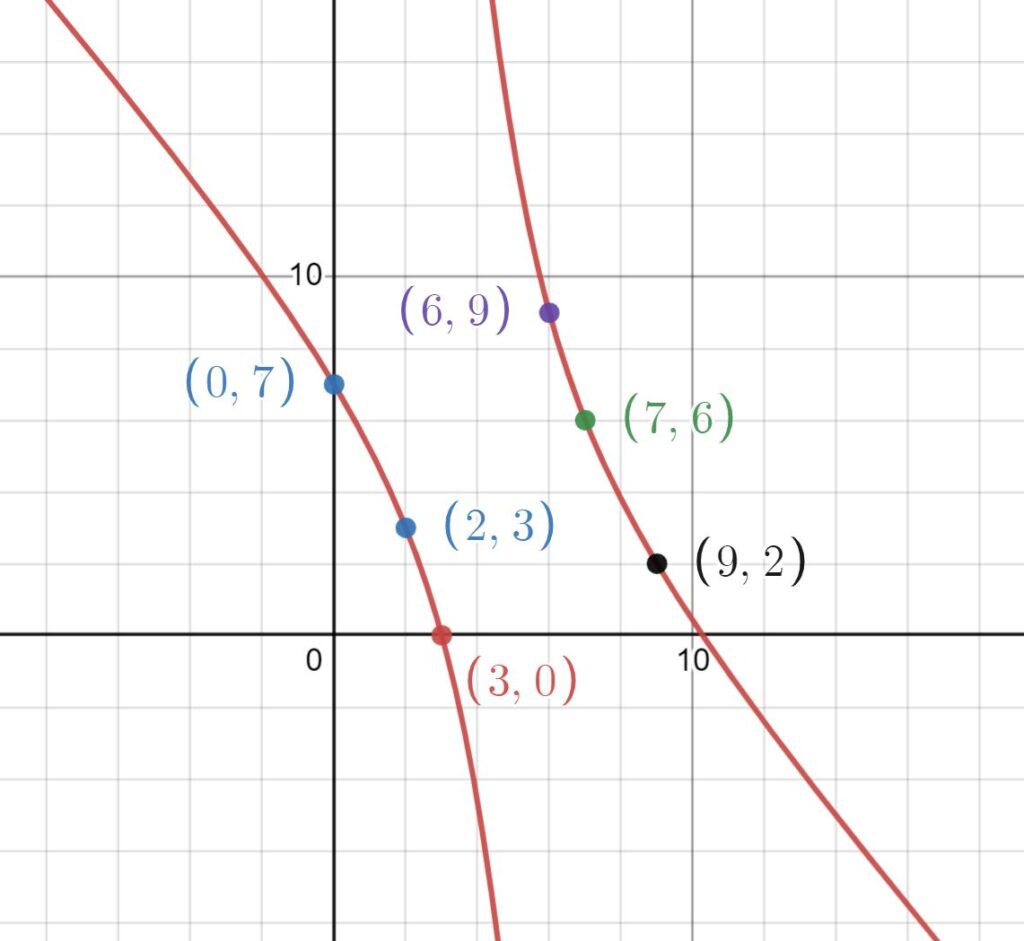
Wells also stated that the points determined by the period of $\frac{1}{13}=0.076923076923….$ lie on a hyperbola. To find the equation of this conic, I contacted Professor Marc Chamberland – a co-author of the paper ‘A Generalization of the One-Seventh Ellipse‘. Marc sent this explanation in his reply:
Using the notation from our paper, we let $a=0, b=7, c=6$ and $S=9$. Theorem 1 implies that the points $(0,7), (7,6), (6,9), (9,2), (2,3)$ and $(3,0)$ all lie on a conic. Putting these points on the bivariate quadratic curve $Ax^{2} + Bxy + Cy^{2} +Dx + Ey + F = 0$, we can solve for the coefficients: $A = 141, B = 134, C=9, D = -1872, E = -684, F = 4347$.
Marc Chamberland
The conics were a huge and fascinating surprise but I don’t know if there is any conclusion or use for their connection to the cycles. However, there is a connection to the final part of the Pascal pentalogy as the paper A Generalization of the One-Seventh Ellipse makes use of Pascal’s Hexagrammum Mysticum Theorem.
Further reading
If you’ve found this interesting, the following links are intended for any reader wishing to look further into the content:
- In particular, I recommend Tony Padilla’s Numberphile video explaining how the cyclic permutations are formed.
- MacTutor biography of Dattatreya Ramachandra Kaprekar, which includes some more number patterns
- You can read more about Cyclic numbers, Midy’s Theorem, Artin’s Constant and the general bivariate quadratic curve at Wolfram MathWorld.
I’ve got a headache
This is amazing stuff! I’ve added a link to my “Super Sevens” post: https://karendcampe.wordpress.com/2021/07/14/super-sevens/
Thanks!
Thank you, Karen
This is far out. It’s like discovering exciting archaeology inside the realm of numbers.
There’s also an excellent collection of links worth following up.
In the magic square, all the row and column sums match because addition is commutative. The same numbers appear in each row and column (in various permutations); this is true for a square made from the fractions of any cyclic number, not just 19.
It is cute that the diagonal sums also match in the example shown here. The next such instance is a square built from fractions with denominator 383, where each {row,column,diagonal} sums to 1719.
Thanks for the 1/383, Tom