(A report by Richard Elwes from the launch of the London Mathematical Society’s 150th birthday year. All the talks are available to watch online at the LMS’ birthday portal)

There’s a standard format for celebrating a mathematical milestone, perhaps the 80th birthday of some deeply eminent number theorist. His collaborators and graduate students, and their graduate students, and their graduate students all gather together in some gorgeous location to regale each other with their latest theorems, while the rest of the world pays no attention. For the London Mathematical Society’s birthday, we had something different. Well, we did have the gorgeous location. The Goldsmiths’ hall in London is a magnificent venue, and the livery hall in particular was evidently designed by someone with a peculiar fondness for Element 79. (See for yourself.) But speaker-wise, a decision had obviously been taken that the party would be an outward-looking affair. The focus was not so much on the LMS, or even on maths per se, but on our subject’s ability to unlock worlds, particularly the worlds of TV, film, and computer games.

The event was hosted with great panache by Maggie Philbin, everyone’s favourite Tomorrow’s World presenter and, as one of the first journalists to try a mobile phone, probably the first person ever to shout “I’m on the train!” down a comically outsized device.

A recurring theme through the day was that other proud British institution which has recently celebrated a major birthday: Doctor Who. After a greeting from the current LMS president Terry Lyons, the day’s first speaker was Steve Thomson, a former maths teacher and one of the Doctor’s script-writers. (He has also wielded his pen for Sherlock and in other honourable causes.) Steve described how mathematical ideas can spice up these stories. These applications are all rather gentle: the non-Euclidean geometry of the corridors of the TARDIS (Series 6, Episode 4, The Doctor’s Wife), naming Time Lord technology with randomly selected mathematical buzzwords (DOCTOR: “The parametric engines are jammed! Orthogonal vector’s gone! I’m almost out of ideas!”, Series 6, Episode 3, Curse of the Black Spot), and so on. Omitted from the talk, as Yemon Choi pointed out on Google plus, were Block transfer computations: mathematical operations so powerful that performing them alters the structure of space-time.

The quaternions provided a second recurring theme. These strange 4-dimensional numbers were invoked by the second speaker, the mathematician Nigel Hitchin, as one of several delightful tales of mathematical Creativity, Discovery, and Curiosity. Their discoverer, William Hamilton, was impressed by the complex numbers as a 2-dimensional number system, but was adamant that he could go one better. As it happened, he went two better, and famously carved the axioms for his system on Broom Bridge in Dublin (a plaque still marks the spot). He became so obsessed with these objects that he came to believe, or so it was said, that they could solve every problem presented by the real world, an affliction his critics dubbed “Irish madness”.

His discovery received a luke-warm reception at the time, with Lord Kelvin bitchily remarking: “Quaternions came from Hamilton after his really good work had been done; and, though beautifully ingenious, have been an unmixed evil to those who have touched them in any way”. All the same, quaternions have subsequently proved themselves useful, both within mathematics and, as we heard later, in engineering. From this story, Nigel drew the moral that “curiosity driven research is certainly worth pursuing, but you may have to wait 150 years in order to see the fruits of it”.

For me, Rob Pieké from the Moving Picture Company delivered the day’s stand-out presentation, describing how to create fluid special effects in films. Smoke, dust, and flame all count as fluids, so imagine, let’s say, a giant monster made of molten lava smashing a mountain to bits. It is obviously important that the resulting plume of dust be visually realistic, otherwise how can the audience possibly believe what they’re seeing? (See MPC’s film reel for other similar examples.)

A fire-breathing lava monster, yesterday.

First you divide the space into tiny cubic boxes called voxels. Then inject some virtual fluid, and encode in each voxel simplified versions of the Navier-Stokes laws of fluid dynamics. For instance, since fluids are assumed to be incompressible, the amount of fluid flowing into each voxel through its six faces should be equal to the amount flowing out. But once you’ve adjusted the outflow to make this true at one voxel, you may have messed up the neighbouring one. Bring in the heavy duty computers: you simply iterate this correction procedure until it stabilises, or near enough. Robert gave such an exquisitely clear exposition of this process that by the end of his talk I almost felt that I could go and code up a simulation myself. His advice: “Try it, it’s a good weekend project if you already have the right framework in place (i.e., grid/voxel lib, image writer)”. So next time you’re in the cinema watching a two-headed winged dog creature breathing fire, remember to say a little thank you to the mathematicians in your life for that amazingly authentic nasal smoke.

Another terrific talk followed, from Andrew Blake, Laboratory Director at Microsoft Research Cambridge, and one of the people behind Kinect. His central question was: How can you teach a machine to see? Examples of genuine machine sight include facial recognition in cameras, and pedestrian detection in Mercedes. The particular problem he and his colleagues were faced with was getting a computer to see a human body. Needless to say, human bodies come in many shapes and sizes, can adopt a number all manner of contorted poses, and camouflage themselves in all sorts of inconvenient ways. The team used machine learning techniques to teach the computer to recognise the different parts of the body, with sophisticated ideas from information theory serving to home in on the right answer with high probability and within a manageable time. (One of their crowning triumphs was to use their device to create a 3D scan of the graph theorist Béla Bollobás.)

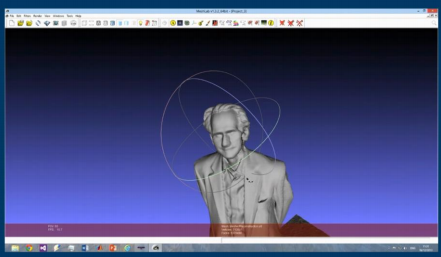
The 3D scan of Béla Bollobás, from Andrew Gibb’s lecture on the subject

Robert Calderbank spoke next and again invoked the quaternions, this time to highlight the difficulty of distinguishing between pure and applied maths. Robert (who has won several awards for his decisive contributions to mobile phone technology and related areas) admitted that he is not clever enough to be able to tell the difference, and, goodness knows, nor am I. GH Hardy, who is not known as an idiot, famously got it completely wrong, writing in his Apology “I have never done anything ‘useful’. No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world.”

Nowadays quaternions sit within the broader context of matrix algebra. In this modern incarnation, Robert explained that they provide exactly the right formalism for encoding telephone calls across two channels, giving a much more robust signal than either could achieve alone. So much, then, for “pure” mathematics.

The Doctor regenerated for the next talk by James Reid, Head of Effects at Milk, who talked about mathematical ideas in the artistic side of special effect design. So, imagine you’re a Dalek exterminating the residents of Arcadia (The Day of the Doctor, 50th Anniversary Episode). The question is: when you blow up a Gallifreyan building, how should it fragment, so as to look most realistic? Obviously, splitting it into little cubes would look rubbish. The answer (I’m reconstructing the idea here, since James didn’t go into much detail – any errors are mine) is to use a Voronoi partition. You might start by randomly distributing nodes around the virtual building. Then every location in the building sticks with its nearest node, and when the whole thing comes apart those are the lovely irregular chunks that you see. This simple, attractive idea has numerous applications throughout science (and not only if you’re an insane genocidal pepper-pot).

The final talk came from Frances Kirwan, a former president of the LMS (and, as it happens, my algebra lecturer from about 15 years ago). Lest we forgot what we were all doing there, she finished the day with a short account of the history of the LMS. We learnt that the society is the world’s third oldest surviving national mathematical society (props to the Dutch and Moscow Societies), that it was founded in 1865, and that the inaugural president was Augustus de Morgan. It more or less took the reins from the Spitalfields Mathematical Society which had been running for the previous 150 years or so, where maths and merriment cheerfully mixed, and “every member had his pipe, his pot, and his problem”. You can read the lyrics to the Spitalfields society drinking song online, at Songs from the History of Science. It’s all about how alcohol makes you a better scientist. Here’s a taster:

“When Ptolemy, now long ago,
Believed the earth stood still, Sir,
He never would have blundered so,
Had he but drunk his fill, Sir”.

At the early LMS meetings, in contrast, De Morgan commanded that not a drop of liquor should be seen.

As well as banning the booze, another LMS innovation was to admit women from the start (unlike other learned societies I shall resist naming and shaming), with Ada Lovelace being an early member. (Ada has multiple claims to fame: the poet Lord Byron’s daughter, she was the Countess of Lovelace, Augustus De Morgan’s maths student, and as Charles Babbage’s collaborator, was arguably the world’s first computer programmer. What is more it’s her 200th birthday this year. Happy birthday Ada!).

Some other LMS factoids: Mary Cartwright was the first female president; GH Hardy is the only person to have been president twice; another president, Henry Whitehead, claimed to do his best mathematical work while talking to his pigs. Furthermore, and in the spirit of the day, it has always been a firmly outward-looking society, with many of the greatest mathematicians from beyond these shores honorary members: Cantor, Hilbert, Poincaré,…

And on that note, and with Misery De Morgan’s stricture consigned to the dustbin of history, the assembled company wandered out for birthday cake in another room apparently constructed from solid gold. The reception was opened by Pavel Exner, president of the European Mathematical Society, which is also celebrating a major milestone this year: its 25th birthday. (Disclaimer: I’ve recently become the EMS’s publicity officer, so can’t not mention that!)

The final thing to say (apart from the fact that we ate beetroot flavoured meringues at some point, which were strangely delicious) is that this event was only the launch of the 150th anniversary celebrations. Events are continuing throughout the year, and throughout the country. You can find more details on the LMS’s events listing page.

Lastly then: Happy Birthday to the LMS! (And to the EMS, to Ada Lovelace, and, belatedly, to Doctor Who.)