This is a guest post by mathematician and maths communicator Ben Sparks.
Roger Apéry: 14th November 1916 – 18th December 1994
100 years ago (on 14th November) was born a Frenchman called Roger Apéry. He died in 1994, is buried in Paris, and upon his tombstone is the cryptic inscription:
\[ 1 + \frac{1}{8} + \frac{1}{27} +\frac{1}{64} + \cdots \neq \frac{p}{q} \]
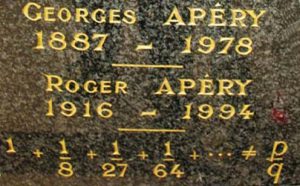
Apéry’s gravestone – Image from St. Andrews MacTutor Archive

Roger Apéry – Image from St. Andrews MacTutor Archive
The centenary of Roger Apéry’s birth is an appropriate time to unpack something of this mathematical story.
Let’s start with something relatively simple:
What happens if you add up all the unit fractions?
\[ \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \cdots \]
Answer? Not a lot.
Or, rather more accurately – a lot. This is the tolerably well-known harmonic series, and it is relatively easily demonstrated that it diverges, or as you might like to think of it, has an infinitely large answer.
Now do the same thing with the unit fractions with squares in the denominator:
\[ \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \frac{1}{6^2} + \cdots \]
It may be something of a surprise, when first encountered, that this time the sum converges – and has a well-defined answer, which is in fact: $\frac{\pi^2}{6}$. Proving this is known as the Basel Problem, and was first demonstrated by Leonhard Euler in the 18th century. It also turns out to be the reciprocal of the answer to the question:
“What is the probability that two positive integers selected at random are relatively prime?”
Moving on one more step, what happens if you use the cubes instead of the squares.
\[ \frac{1}{1^3} + \frac{1}{2^3} + \frac{1}{3^3} + \frac{1}{4^3} + \frac{1}{5^3} + \frac{1}{6^3} + \cdots \]
This time nothing is very obvious. It is tempting to believe immediately that this too will converge, since the squares version did (and in fact, this is correct) but it is certainly not clear what it might converge to. Mathematicians made some progress (including Euler again, who calculated the first 16 decimal digits of the sum), arriving at the conclusion that
\[ \frac{1}{1^3} + \frac{1}{2^3} + \frac{1}{3^3} + \frac{1}{4^3} + \frac{1}{5^3} + \frac{1}{6^3} + \cdots \simeq 1.2020569\ldots \]
But what is this number? Will the decimals repeat or end (i.e. – is it a rational number)?
Nobody knew – until a French mathematician named Roger Apéry made an announcement in 1978, followed by some clarifications in 1979 (for a surprised mathematical community). He had proved that this number is indeed irrational. As a result, it is now known as Apéry’s constant.
What is more, this sort of result has proved extremely difficult to produce. The examples we have been looking at are all particular examples of the Riemann Zeta Function:
\[ \zeta(s) = \sum_{n=0}^{\infty} \frac{1}{n^s} \]
The harmonic series is $\zeta(1)$, the sum of the reciprocals of the squares is $\zeta(2)$, and Apéry’s sum is $\zeta(3)$. To put these in context, it is currently not known specifically whether any other particular $\zeta(n)$, for $n$ odd, is irrational. The best we’ve got is from Wadim Zudilin, in 2001, who showed that at least one of $\zeta(5), \zeta(7), \zeta(9), \zeta(11)$ must be irrational, and Tanguy Rivoal, in 2000, who showed that infinitely many of the $\zeta(2k+1)$ must be irrational.
It is also not known whether Apéry’s constant is transcendental.
But it is the reciprocal of the answer to the question:
“What is the probability that any three positive integers selected at random are relatively prime?”
Hooray!
More information
Some Classical Maths Blog – a review of Apery’s proof and some pdfs of the original
Rivoal, Tanguy (2000), “La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs”
Zudilin, Wadim (2001), “One of the numbers ζ(5), ζ(7), ζ(9), ζ(11) is irrational”
I understand what is meant in the probabilistic statements, but have always wondered how you would formally write down: picking a random positive integer.