This post is in response to Peter’s post introducing the Approximate Geometric Mean.
The approximate geometric mean $\mathrm{(AGM)}$ is a nice approximation of the geometric mean $\mathrm{(GM)}$, but it has some quirks as we will see. After a discussion at the MathsJam gathering, I was intrigued to find out how good an approximation it is.
To get a better understanding, we first have to look again at its definition. For $A=a\cdot 10^x$ and $B=b \cdot 10^y$, we set
\[ \mathrm{AGM}(A,B):=\mathrm{AM}(a,b)\cdot 10^{\mathrm{AM}(x,y)} \]
where $\mathrm{AM}$ stands for the arithmetic mean. This makes also sense when $a$ and $b$ are not just integers between 1 and 10, but any real numbers. Note that we won’t consider negative $A$ and $B$ (i.e. negative $a$ and $b$), as the geometric mean runs into issues if we do so. The values of $x$ and $y$ may be negative, though. The $\mathrm{AGM}$ looks like a mix between the $\mathrm{AM}$ and the $\mathrm{GM}$, so what can possibly go wrong?
Same mean, different numbers
In contrast to the $\mathrm{AM}$ and the $\mathrm{GM}$, the $\mathrm{AGM}$ depends on the number base (10 in this case) and the presentation of $A$ and $B$.
If we write $A=(10a) \cdot 10^{(x-1)}$, we get a different value for $\mathrm{AGM}(A,B)$. This looks rather unfortunate, but it will turn out to be helpful. To ease notation we will assume in the following that $a\geq b$ unless otherwise stated. This can be done without loss of generality as $\mathrm{AGM}(A,B)=\mathrm{AGM}(B,A)$.
Peter Rowlett proved in his post that $\mathrm{GM}\leq \mathrm{AGM}$. The question is, how far can the $\mathrm{AGM}$ exceed the $\mathrm{GM}$? In other words, what’s the supremum of the ratio $R=\mathrm{AGM}/\mathrm{GM}$?
Using the notation of $A$ and $B$ as above we get
\[
\begin{align*} R=\frac{\mathrm{AGM}(A,B)}{\mathrm{GM}(A,B)}= \frac{\mathrm{AM}(a,b)}{\mathrm{GM}(a
\]
So, the ratio $R$ doesn’t depend on $x$ and $y$ but only on $a$ and $b$. That’s convenient. Taking $a$ and $b$ in the interval $[1,10)$, as is usual, we can look at the plot of $R(a,b)$.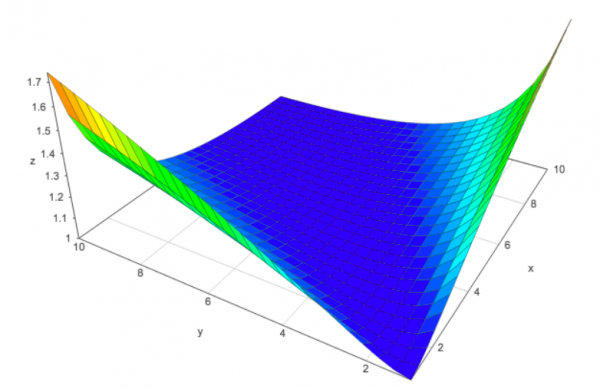
As long as we are in the blue part of the graph, $\mathrm{AGM}$ looks to be a sensible approximation of the $\mathrm{GM}$. So let’s look at the bad combinations of $a$ and $b$.
The worst case happens when $a$ and $b$ are maximally far apart: The supremum of $R(a,b)$ is its limit for $a \rightarrow 10$ and $b=1$. So in general, $1\leq R \lt 5.5/\sqrt{10} \approx 1.74$.
This supremum doesn’t look too bad at first, but unfortunately, the result can be unusable in extreme cases. For example, if $a=999=9.99\cdot 10^2$ and $b=1000=1 \cdot 10^3$, we have $\mathrm{GM}(A,B)\approx \mathrm{AM}(A,B)=999.5$ and $\mathrm{AGM}(A,B)\approx 1738$ – not only is the $\mathrm{AM}$ a better approximation of the $\mathrm{GM}$ than the $\mathrm{AGM}$ in this instance, the $\mathrm{AGM}$ is bigger than both the numbers $A$ and $B$ of which it is supposed to give some kind of mean!
Let’s analyse this a bit deeper. The ratio $R$ only depends on the ratio $r=a/b$. In closed form we can write $R(r)=1/2\cdot (\sqrt{r}+\sqrt{r}^{-1})$ and we are left to study this function in the range $[1,10]$. Its maximum is $R(10)$, but smaller $r$ give better results. And we will see, that we don’t have to put up with $r=10$.
Here, the flexibility of the definition of the $\mathrm{AGM}$ comes into play. Due to the choice of a suitable presentation of the numbers we can guarantee that $r$ isn’t too big. If we have $r\leq \sqrt{10}$ which is equivalent to $\sqrt{10}b\geq a \geq b$ we calculate $\mathrm{AGM}(A,B)$ as above. If $a>\sqrt{10}b$, we change the presentation of the number:
\[
\begin{align*}B=b \cdot 10^y = (10b)\cdot 10^{y-1}=:b’ \cdot 10^{y-1} \end{align*}
\]
and continue from there.
So, let’s redefine the $\mathrm{AGM}$ for $10>a\geq b\geq 1$ like this:
\[
\begin{equation}
\mathrm{AGM}(A,B)=\begin{cases}
\mathrm{AM}(a,b)\cdot 10^{\mathrm{AM}(x,y)}, & \sqrt{10}b\geq a,\\
\mathrm{AM}(10b,a)\cdot 10^{\mathrm{AM}(x,y-1)}, & \text{otherwise}.
\end{cases}
\end{equation}
\]
Note, that in the second case we have $\sqrt{10}a>10b>a$, so that the roles of the pair $(a,b)$ are taken over by the pair $(10b,a)$. Setting $r=10b/a$ in the second case, we have in both cases $1\leq r\leq \sqrt{10}$, so we only have to study $R(r)$ in the interval $[1,\sqrt{10}]$, which will turn out to be rather benign.
Note also, that this new $\mathrm{AGM}$ can still be calculated without a calculator when using the approximation $\sqrt{10}\approx 3$, as Colin Beveridge suggested in Peter’s post.
In the example above with $A=999$ and $B=1000$ we write $B=10\cdot 10^2$ and find with this new definition of the $\mathrm{AGM}$:
\[
\begin{align*}\mathrm{AGM}(999;1000)=\mathrm{AM}(9.99;10) \cdot 10^{\mathrm{AM}(2;2)}=999.5, \end{align*}
\]
This coincides with the arithmetic mean of the two numbers and is really close to the geometric mean. This is looking promising.
If we define the $\mathrm{AGM}$ of two numbers $A$ and $B$ in the way explained above, we get the following two inequalities:
\[
\begin{align*} (I) \quad & \mathrm{GM}(A,B)\leq \mathrm{AGM}(A,B) \leq \mathrm{GM}(A,B) \cdot 1.2 \\
(II) \quad & \mathrm{GM}(A,B) \leq \mathrm{AGM}(A,B) \leq \mathrm{AM}(A,B) \end{align*}
\]Both inequalities together mean that not a lot can go wrong when using the $\mathrm{AGM}$ with the appropriate presentation of the numbers: The $\mathrm{AGM}$ is bigger than the $\mathrm{GM}$, but exceeds it by maximally 20%, and it is always smaller than the $\mathrm{AM}$.
As a consequence, the $\mathrm{AGM}$ will always be between $A$ and $B$. So it is indeed a “mean” of some kind.
A proof of these two inequalities
(I) We only have to find the maximum of $R=\mathrm{AGM}/\mathrm{GM}$. Due to the discussion above we can assume that $\sqrt{10}b\geq a \geq b$, but $a$ can now be bigger than 10. The latter is not a problem though.
The maximum of $R=\mathrm{AGM}(A,B)/\mathrm{GM}(A,B)=\mathrm{AM}(a,b)/\mathrm{GM}(a,b)$ is attained when $a$ and $b$ are maximally apart, i.e. $r=\sqrt{10}$, so
\[
\max\left(\frac{\mathrm{AGM}(A,B)}{\mathrm{GM}(A,B)}\right)=\frac12 \cdot (10^{1/4}+{10^{-1/4}}) \approx 1.2.
\]
(II) We will show that $\mathrm{AGM}(A,B)/\mathrm{AM}(A,B) \leq 1$. Let’s drop the assumption that $a\geq b$. Instead we assume, again without loss of generality, that $x\geq y$, so that we can set $z=:x-y \geq 0$. For the ratio $r=a/b$ we have $\sqrt{10} \geq r \geq 1/\sqrt{10}$. If $r$ fell outside this interval, we would have had to change the presentation of one of the numbers before calculating the $\mathrm{AGM}$. Dividing the numerator and denominator in the above inequality by $B$ we get:
\[
\frac{\mathrm{AGM}(A,B)}{\mathrm{AM}(A,B)}=\frac{(1+r) \cdot 10^{z/2}} {1+r \cdot 10^z}.
\]
So we look for an upper bound of the function $f_z(r):=\frac{(1+r) \cdot 10^{z/2}} {1+r \cdot 10^z}$ when varying $z$ and $r$ and want to show that this upper bound is smaller or equal to 1. Note, that we only have to check for integer $z\geq 0$ (The result is actually false if we allow any real $z$).
For $z=0$, we have $f_0(r)=1$ for any $r$ and hence $\mathrm{AGM}=\mathrm{AM}$. For a fixed $z \geq 1$ we can derive the function $f_z(r)$ with respect to $r$ and find that the slope is always negative. Hence for a fixed $z$, the function $f_z(r)$ attains a maximum when $r$ is smallest, i.e. $r=1/\sqrt{10}$, so we are left to show that
\[
f_z(1/\sqrt{10})=\frac{(1+10^{-1/2})10^{z/2}}{1+10^{z-1/2}}\leq 1.
\]
For $z=1$ we have equality again and $\mathrm{AGM} = \mathrm{AM}$. For $z\geq 2$ we can write $z=2+z’$ with $z’$ being an integer $\geq 0$. We get the following chain of inequalities
\[
f_z\left(\frac{1}{\sqrt{10}}\right)=\frac{(1+10^{-1/2})10^{(2+z’)/2}}{1+10^{3/2 + z’}}<\frac{2\cdot 10^{1+z’/2}}{10^{3/2+z’}}\leq \frac{2}{\sqrt{10}}<1.
\]
This proves the second inequality. ☐
In summary, modifying the definition of the $\mathrm{AGM}$ to assure that the ratio of the “leading characters” is as close to 1 as possible, makes sure that the $\mathrm{AGM}$ works well, even in the bad cases.
One Response to “Taming the AGM”