This is a roundup of things which happened at Manchester MathsJam, February 2012.
First, we discuss a puzzle I found on Futility Closet, a blog of curiosities by Greg Ross which is sometimes mathematical. The Martian Census Bureau compiled the marital history of every male and female Martian, living and dead: Never married: 6,823,041; Married once: 7,354,016; Married twice: 1,600,897; Married three times: 171,013; Married four times: 2,682. What’s wrong with these figures?
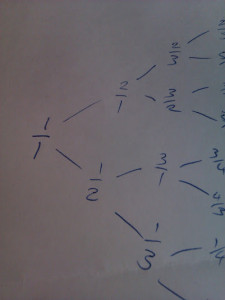Paul points out a fact he read on Colin Wright’s blog recently: that if you write a fraction $\frac{a}{b}$, and from it draw two branches at the ends of which are $\frac{a+b}{a}$ and $\frac{a}{a+b}$, a tree formed in this way starting from $\frac{1}{1}$ will give all rational numbers exactly once, and always written in their lowest terms. Lovely!
A puzzle comes through from Leeds MathsJam: there are a set of chameleons, 13 red, 15 blue and 17 green. When two chameleons of different colours meet, they both change to the third colour (when two chameleons of the same colour meet, nothing happens). The question is, can they ever all become the same colour. Paul works it out using modular arithmetic.
Another puzzle from East Dorset MathsJam: the following sequence is in strictly increasing numerical order: $x, x^3, x^4, x^2, x^0$. Where does $-x^{-1}$ fit in the sequence? I enjoy solving it quite a lot.
There is a brief discussion as to how to prove that $0! = 1$, to anyone doubting. Paul points out that $\frac{n!}{n} = (n-1)!$, and hence $\frac{1!}{1} = 0!$, and as it’s agreed that $1!=1$, the result follows. Someone else suggests a proof using the binomial formula: ${n \choose r} = \frac{n!}{r!(n-r!)}$, and if $n=r$ there’s one way to choose a number of things from that many things. So, the only way this equation can be satisfied is if $(n-r)! = 0! = 1$.
A couple of games of Continuo take place. It’s a tabletop game involving a set of cards, each square and divided into 16 sub squares, coloured using red, yellow, blue and green in set layouts. The aim is to place a card on your turn which produces the maximum amount of long chains of squares of the same colour, and your score is the sum of all chains of length 2 or more made by your turn. It’s quite fun to play and the opportunity to point out others’ options before they place is irresistible to onlookers. Afterwards, we discuss whether all possible combinations of the four colours are represented within the deck, given that the layout is always the same and a given card contains two, three or four colours but no two adjacent sections are the same colour. We agree there are 84 possible combinations including symmetry, and as each piece has a rotational symmetry of order 2, that means they’re all there.
Steve, who’s here for the first time, suggests a puzzle he got from Mensa magazine many years ago. There are a number of aliens in a room, and each alien has a number of fingers on each hand (more than one). If you knew the total number of fingers in the room, then you would know the total number of aliens in the room. There are between 200 and 300 fingers in the room. How many aliens are there? We briefly become convinced it’s impossible, and I search online to see if there’s a version that’s better stated, as Steve has left by this point. We’re convinced you need some extra info, like how many hands they have, or whether the number of fingers on each of their hands is the same. It turns out the key fact he’d missed was that all aliens have the same number of fingers as each other, and all aliens have a different number of fingers on each hand. In this case, the answer has to be the square of a prime in order for you to know unambiguously how many aliens there are. We still don’t really like it, as you need to state too many facts to make it a well defined puzzle.
Can you make 25 using the numbers 2,4,6 and 8 and standard ‘Countdown’-style arithmetic operations?
Some time is spent discussing the issue of whether it’s possible to place 5 white queens and 5 black pawns on a chessboard so that all the pawns are safe from attack by the queens. This puzzle is being discussed at several MathsJams, having been posed by Glasgow MathsJam. We find it to be quite easy, until it’s made clear we’re talking about a $5 \times 5$ chessboard. At this point it’s agreed further research is needed.
“I have three children”, states a puzzle, “Can you guess their ages? The sum of their ages is 13; the product of their ages is your age; and my eldest child plays piano. Now you can tell me their ages.” How old are the children?
Ben introduces his new form of notation for large numbers. He defines a set of operators called $(1), (2), (3),\dots$ such that $x(1)y = x+y,$ $x(2)y = x \times y,$ $x(3)y = x^y,$ and so on. He wonders if this would be a more efficient way to represent large numbers, and wonders what Graham’s number would be in this notation. We discuss arrow notation (I look up what it is online as no-one can remember properly) and write down Graham’s number in arrow notation. We agree that what Ben has invented is equivalent to arrow notation somehow, in that the number in the centre is related to the number of arrows you’d draw.
At the end of the night, someone mentions black and white hats, and experiencing Logic Puzzle Overload, Andrew draws a cartoon of a three-armed alien wearing a black hat, being married by a priest to a chameleon in a white hat, attended by queens and pawns. The chameleon is wondering what colour to turn.
