Dear Mathematician,

My partner and I are trying to buy a house. We both work in different places, and neither of us enjoys commuting. How could we decide where to live?

Fictionally yours,

Norman Mettrick

Norman,

Thank you for your intriguing and entirely imaginary letter. The short and not terribly useful answer would be: exactly halfway between your two workplaces. This doesn’t leave you with many options, if any, so let’s try to build up to something more useful.

The fact that neither of you enjoys commuting suggests you want a solution that’s fair on both of you. If you get out a map and find the midpoint with your ruler and compass in the standard classroom method, you’ll have already found a perpendicular bisector. This line gives you points equidistant to each of your workplaces (actually a great circle, since I didn’t notice a Flatland postmark on your envelope).

This second solution is still very fair, and gives you a whole extra dimension of choice, but still fails to be practical for several reasons:

• You probably want to limit how far you both have to travel, as pleasant as living on the opposite side of the Earth could be.
• You’re probably more interested in how long it takes you to travel, rather than how far. Measuring the Euclidean distance from your workplaces is not terribly useful for this, unless you’re both farmers walking across a featureless rural idyll, or not-so-secret agents driving hijacked tanks to your respective offices, with little regard for traffic or architecture.

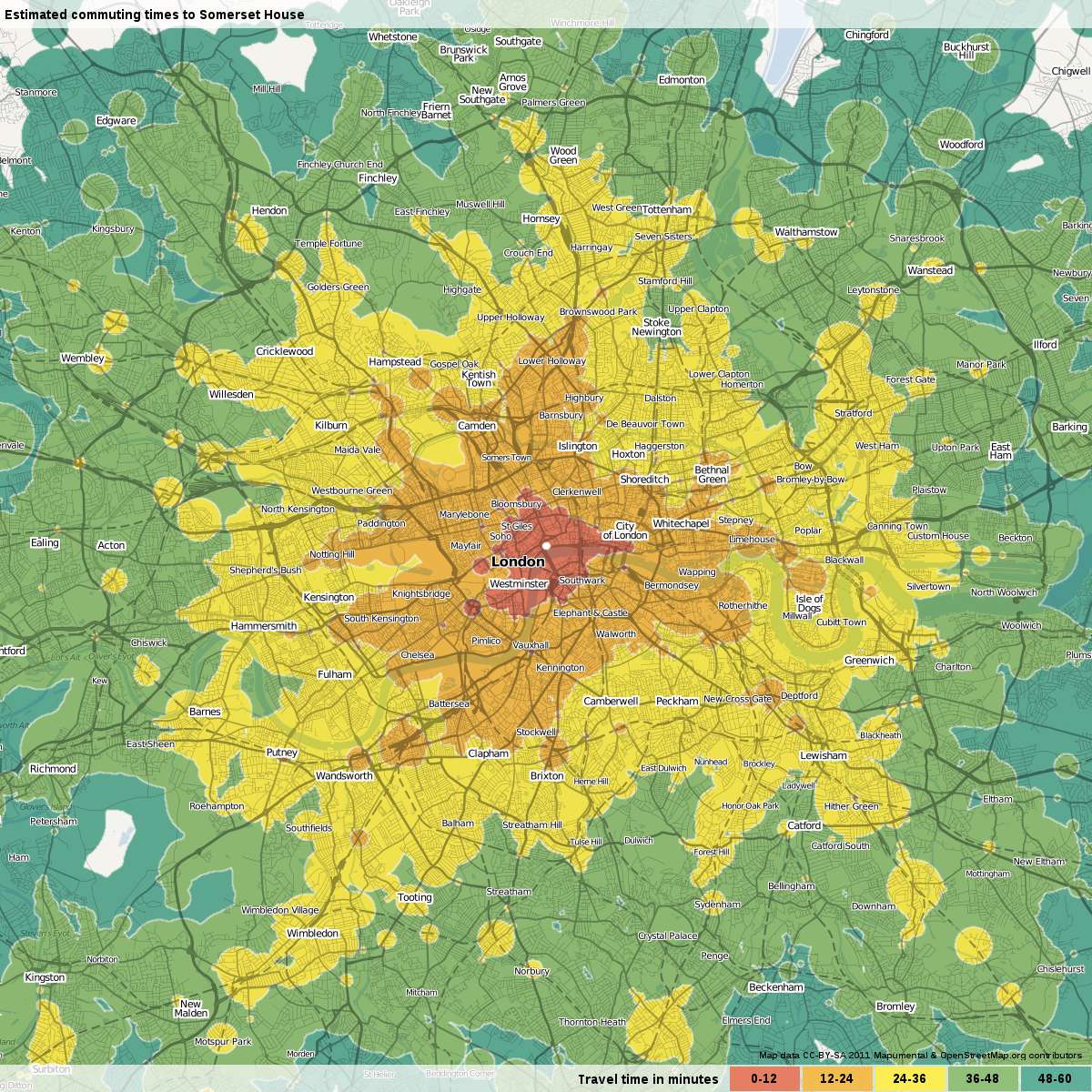
A map of commuting times looks more like the following image than a series of perfect circles.

You can buy or create such maps to help you narrow down your search, but if you already have a selection of houses in mind, then I suggest the following: whenever you collect a house advert, temporarily, on a piece of scrap paper, scrawl down both of your travel times. We’ll look at various ways of combining those values into an aggregated commuting toll for the house. You can pick your favourite method, and use it to calculate this toll and neatly write it down on the advert below the asking price and other such properties of the property. However, you always should pick a method to combine them before you check the specific commuting times: you wouldn’t want to be accused of coming to a biased decision.

We’ve seen that absolute fairness of outcome can be very restrictive, so you might be tempted to try a free market solution. If you had written to an economist instead, they may have offered to set you up some kind of auction. This may be a good way to decide who gets what bedroom in a student houseshare, but couples hopefully have each other’s best interests at heart, and, if you’re planning to buy a house together, you’re probably already sharing money to some extent, which would make such an auction a bit pointless.  You could, however, agree to offset the shorter travel time with some amount of housework.

Bearing that in mind, we will maintain some fairness. Each of the measures of commuting pain for each house will be an aggregate that does not inherently favour either party’s interests in general: they’ll be in some way symmetrical. Take the bit of scrap paper, and label one of the commuting times $t_a$ and the other $t_b$. These will be different for each house, so for a house at location $z$, you could write $t_a(z)$ and $t_b(z)$.

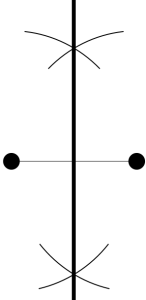
The first method is the easiest: simply write down the larger of the two travel times under the houseprice.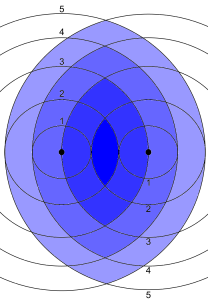

If you try to minimise the travel time without regard to house prices you’ll just get back to one (or several) equitemporal points between the two workplaces. If we return to measuring Euclidean distances, $d_a(z)$ and $d_b(z)$, for illustrative purposes, to get some sense of this measure, you get these lens-shaped areas, $\max\left\{d_a(z),d_b(z)\right\} \leq n$, of steadily increasing household commuting pain.

However, this measure also lacks subtlety. In my opinion, it seems wrong to rate a house more highly which gives two equal commutes of $85$ minutes each, than one with a commute of $90$ minutes for one person and $10$ minutes for the other. It favours the individual, but ignores the pair of you.

To remedy this we could investigate a second option: score the houses by adding the travel times $t_a$ and $t_b$.

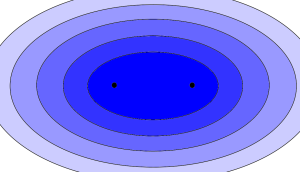
Again, looking at distances as a simple substitute, $d_a(z)+d_b(z)$ gives us a series of ellipses, whose foci are the two places of work. This is fairly straightforward to draw by hand on a map. Take a string whose length is the greatest combined distance the pair of you want to commute (obviously, this must be longer than the distance between your workplaces). Now stick two drawing pins (voodoo-style!) at both offices, pinning the ends of the string to the map. Now, with a pencil, extend the string until it is taut, and draw the outline that keeps the string without slack: the outcome, if you do it perfectly, will be an ellipse.

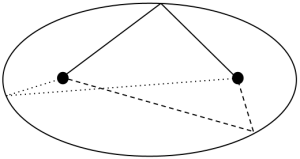
All lines between the foci via the edge of an ellipse (the 'taut string') are the same length.

This method might tell you to save time on your shorter journey by increasing the longer journey: $20$ minutes and $80$ minutes instead of $40$ and $70$ minutes. I wouldn’t consider this to be a particularly fair, but you might disagree. Whoever has their already long travel time extended may feel some resentment towards the other: if they really hate commuting already, housework may not be enough of a bargaining tool to offset it.

My final suggestion is to go between these two extremes. Below each house price, calculate and write out $t_a^2+t_b^2$ (then take the square root, to keep the size and units sensible). This should be a good compromise between limiting the time each of you travel as individuals and the total time the pair of you travels. Now it would take a $9$ and $80$ minute pair to improve on $40$ and $70$ minute commutes: the longer travel time is already so large, it takes an exceptionally short commute to balance it out.

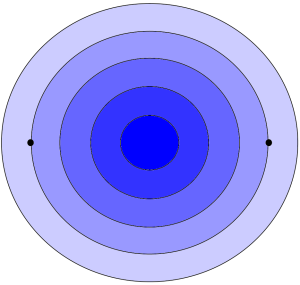
When applied to the geographical distances, it fits well with our intuition, and in fact is also geometrically elegant. Let’s say, without any loss of generality, the two workplaces are at $0$ and $1$ (on the complex plane). If you require the sum of the squares of the travelling distance to be at most $K$, then we need to solve: \[|z|^2 + |z-1|^2=z \overline{z} + (z-1)(\overline{z}-1) \leq K.\]

Rearranging and completing the square gives \[ \left(z-\frac{1}{2}\right)\left(\overline{z}-\frac{1}{2}\right) \leq \frac{K}{2}  – \frac{1}{4}=: R^2,\] which we can rewrite as $\left|z-\frac{1}{2}\right|\leq R$, the equation for a circle centred halfway in between the two workplaces. The resulting map tells us to start looking at the midpoint and fan out the search from there in increasing concentric circles.

If you can’t decide between $t_a + t_b$ and $\sqrt{t_a^2+t_b^2}$, you could always try $(t_a^p +t_b^p)^{1/p}$ for some other value of $p$ where $1 \leq p \leq 2$ (you can consider the discarded method, taking the maximum of the two, to be the $p=\infty$ case). If you’re in a practical mood, you could use public transport APIs to see what these methods would give when applied to real places and travel time data. Or, if you’re feeling more theoretical, you could investigate the shapes resulting from the geometric version when $p=\frac{1}{2}$.

The quickfire answer ‘halfway in-between the two’ had some nugget of truth that held throughout what we did (at least in the distance versions), and allowed us to create a more reasonable answer. Even if you don’t end up using these specific suggestions, at least by discussing them and deciding what would be fair, you may end up saving yourself from a few domestic arguments.

To finish with a related puzzle, from Futility Closet:

An ant will always position itself so that it’s precisely twice as far from vinegar as from honey.
If we put a dab of vinegar and a separate dab of honey on the floor and we release a troop of ants, what formation will they take up?

[peekaboo onshow=”Click to hide solution” onhide=”Click to show solution”]

[peekaboo_content name=”solution”] The army of ants will form a circle that surrounds the honey.

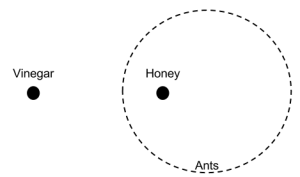
Take the spot of vinegar to be at 0, and the honey at 1 on the complex plane. Then an ant at $z$ must satisfy \[|z|=2|z-1|. \] Squaring and rearranging gives $z \overline{z} – \frac{4}{3}(z+\overline{z}) + \frac{4}{3}$. Finally, completing the square and taking the positive square root gives: \[|z-\frac{4}{3}|=\frac{2}{3},\] a circle with centre $\frac{4}{3}$ and radius $\frac{2}{3}$.

The original puzzle and solution can be found here.[/peekaboo_content]