The building where I work is named after Alexander Stewart Herschel. I suspect this is because it used to be the home of the physics department, since he was an astronomer, but it works for us too because he also has a pretty cool graph named after him.
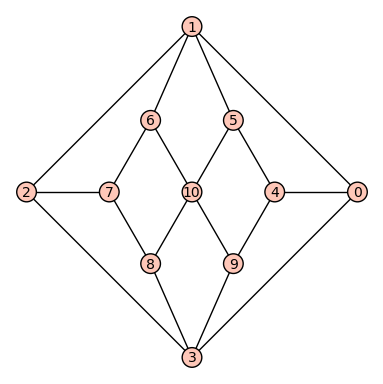
An embedding of the Herschel graph in the plane
Helpfully, it’s called the Herschel graph. It’s the smallest non-Hamiltonian polyhedral graph – you can’t draw a path on it that visits each vertex exactly once, but you can make a polyhedron whose vertices and edges correspond with the graph exactly. It’s also bipartite – you can colour the vertices using two colours so that edges only connect vertices of different colours. The graph’s automorphism group – its symmetries – is $D_6$, the symmetry group of the hexagon. That means that there’s threefold rotational symmetry, as well as a couple of lines of reflection. It’s hard to see the threefold symmetry in the usual diagram of the graph, but it’s there!
Anyway, at the start of the summer, one of the lecturers here, Dr Michael White, told me about this graph and asked if we could work out how to construct the corresponding polyhedron. Making a polyhedron is quite simple – take the diagram on the Wikipedia page, pinch the middle and pull up – but it would be really nice if you could make a polyhedron which has the same symmetries as the graph.

My first attempt at constructing the Herschel enneahedron. It has the obvious reflective symmetry apparent in the diagram, but not the threefold symmetry. Also, two of the faces are missing because I did it all by eye and they were hard to cut out.
We spent an afternoon drawing diagrams and algebra on Michael’s blackboard until we worked out how to do it – arrange three rhombus faces vertically around a central equilateral triangle, then fill in the gaps with six kites – three on the top and three on the bottom. We took a long time (and several coordinate systems) to convince ourselves that the kites really were flat. Now I’ll describe in detail our mathematical argument for the construction we came up with.
The Herschel graph has eleven vertices, three of which have degree $4$; the rest all have degree $3$.
With this embedding of the graph, you can easily see two lines of reflective symmetry, going through vertices $v_1,v_{10},v_3$ and vertices $v_2,v_7,v_{10},v_4,v_0$. But there’s threefold rotational symmetry hidden in there as well!
Look at vertex $v_7$. It’s joined to three vertices each of degree three ($v_2$, $v_6$ and $v_8$), and they’re joined to the vertices of degree four. The same thing happens around vertex $v_4$. You can cyclically permute vertices $v_1,v_3,v_{10}$ and still have a graph which looks the same. That’s threefold rotational symmetry!
We’ve found reflective symmetry of order $4$ and rotational symmetry of order $3$, so all together the graph has a symmetry group of order $12$. It corresponds to $D_6$, the symmetry group of the regular hexagon.
So, how do we make a Herschel polyhedron with these symmetries? It’ll have nine quadrilateral faces – you can see eight closed faces in the embedding of the graph, and the “outside” bounded by vertices $v_1,v_0,v_3,v_2$ closes it off. A polyhedron with nine faces is called an enneahedron.
Start by putting $v_7$ and $v_4$ at the top and bottom. $v_1,v_{10}$ and $v_3$ go in the middle, and need to be arranged in an equilateral triangle to keep the threefold rotational symmetry.
Now, vertices $v_2,v_6$ and $v_8$ need to go somewhere between $v_7$ and the central triangle, and $v_5,v_9$ and $v_0$ need to go between the central triangle and $v_4$. Consider $v_2$. It needs to go on the perpendicular bisector of $v_3$ and $v_{10}$, so we get the first reflective symmetry. The other reflective symmetry is about the central triangle, so it needs to be directly above $v_0$. But $(v_2,v_{10},v_0,v_3)$ is a face of the polyhedron, so it needs to be flat. That means that $v_2$ needs to be directly above the line between $v_3$ and $v_{10}$ (and $v_0$ needs to be the same distance directly below it). We can’t say anything yet about how high it should be.
By symmetry, $v_8$ and $v_6$ need to be directly above the other sides of the central triangle, and at the same height as $v_2$. Similarly for $v_5$ and $v_9$ on the bottom.
With all these constraints, we’ve definitely got three rhombus faces arranged vertically around an equilateral triangle in the middle of the polyhedron. But what about the other faces? Where do $v_7$ and $v_4$ need to be so that the other faces are flat? They definitely need to be above the middle of the central triangle, but how high?
The easiest way we found to work this out was with some vector algebra. Up to the position and scale of the central triangle, we only have two unknowns: the height of $v_2$ and the height of $v_7$. State the coordinates of each vertex in terms of these parameters, and solve!
\begin{align}
\mathbf{h}_1 &= \left(0,0,h_1\right) \\
\mathbf{h}_2 &= \left(0,0,h_2\right) \\
\mathbf{v}_0 &= \frac{\left(\mathbf{v}_1+\mathbf{v}_3\right)}{2} – \mathbf{h}_1 \\
&= \left(\frac{1}{2},0,-h_1\right) \\
\mathbf{v}_1 &= \left(0,0,0\right) \\
\mathbf{v}_2 &= \frac{\left(\mathbf{v}_1+\mathbf{v}_3\right)}{2} + \mathbf{h}_1 \\
&= \left(\frac{1}{2},0,h_1\right) \\
\mathbf{v}_3 &= \left(1,0,0\right) \\
\mathbf{v}_4 &= \frac{\left(\mathbf{v}_1+\mathbf{v}_3+\mathbf{v}_{10}\right)}{3} – \mathbf{h}_2 \\
&= \left(\frac{1}{2}, \frac{\sqrt{3}}{6},-h_2\right) \\
\mathbf{v}_5 &= \frac{\left(\mathbf{v}_{10}+\mathbf{v}_3\right)}{2} – \mathbf{h}_1 \\
&= \left(\frac{3}{4},\frac{\sqrt{3}}{4},-h_1\right) \\
\mathbf{v}_6 &= \frac{\left(\mathbf{v}_{10}+\mathbf{v}_3\right)}{2} + \mathbf{h}_1 \\
&= \left(\frac{3}{4},\frac{\sqrt{3}}{4},h_1\right) \\
\mathbf{v}_7 &= \frac{\left(\mathbf{v}_1+\mathbf{v}_3+\mathbf{v}_{10}\right)}{3} + \mathbf{h}_2 \\
&= \left(\frac{1}{2}, \frac{\sqrt{3}}{6},h_2\right) \\
\mathbf{v}_8 &= \frac{\left(\mathbf{v}_1+\mathbf{v}_{10}\right)}{2} + \mathbf{h}_1 \\
&= \left(\frac{1}{4}, \frac{\sqrt{3}}{4},h_1\right) \\
\mathbf{v}_9 &= \frac{\left(\mathbf{v}_1+\mathbf{v}_{10}\right)}{2} – \mathbf{h}_1 \\
&= \left(\frac{1}{4}, \frac{\sqrt{3}}{4},-h_1\right) \\
\mathbf{v}_{10} &= \left(\frac{1}{2},\frac{\sqrt{3}}{2},0\right)
\end{align}
Now, we want the face $\left(v_1,v_2,v_7,v_6\right)$ to be flat. That’s the same as saying that the four vertices are coplanar. One test of that is:
\[ \left(\mathbf{v_7}-\mathbf{v_1}\right) \cdot \left[\left(\mathbf{v_2}-\mathbf{v_1}\right) \times \left(\mathbf{v_6}-\mathbf{v_7}\right) \right] = 0 \]
Substituting in the co-ordinates for the vertices, we get
\begin{align}
\mathbf{v}_7 – \mathbf{v}_1 &= \left(\frac{1}{2},\frac{\sqrt{3}}{6}, h_2\right) \\
\mathbf{v}_2 – \mathbf{v}_1 &= \left(\frac{1}{2}, 0, h_1\right) \\
\mathbf{v}_6 – \mathbf{v}_7 &= \left(\frac{1}{4}, \frac{\sqrt{3}}{12}, h_1-h_2\right) \\
\\
\left(\mathbf{v}_2-\mathbf{v}_1\right) \times \left(\mathbf{v}_6-\mathbf{v}_7\right) &= \left(-\frac{h_1 \sqrt{3}}{12}, -\frac{3h_1}{4} + \frac{h_2}{2}, \frac{\sqrt{3}}{24}\right) \\
\left(\mathbf{v_7}-\mathbf{v_1}\right) \cdot \left[\left(\mathbf{v_2}-\mathbf{v_1}\right) \times \left(\mathbf{v_6}-\mathbf{v_7}\right) \right] &= -4h_1\frac{\sqrt{3}}{24} + 3h_2\frac{\sqrt{3}}{24}.
\end{align}
All that is equal to zero if the points are coplanar, so:
\begin{align}
-4h_1\frac{\sqrt{3}}{24} + 3h_2\frac{\sqrt{3}}{24} &= 0 & \iff \\
3h_2 &= 4h_1 & \iff \\
h_2 &= \frac{4}{3}h_1.
\end{align}
That means we can make the solid as tall as we like, as long as the two heights remain in the same ratio. Groovy!
After all that algebra, all that was left was to make a model of our Herschel enneahedron.
I’ve never done any 3d stuff on the computer, so I didn’t know where to start. Michael’s new PhD student Ji bravely wrote out a gnuplot script, but the gnuplot 3d renderer is painfully slow, and we couldn’t work out how to make it draw it so it looked how we imagined. A few days ago, William Stein announced that he’d got 3d rendering working in the Sagemath Cloud. Sage is a really good project, an open-source competitor to systems like Mathematica and Maple, and the Sagemath Cloud is an amazing feat: it’s the whole Sage system, running over the internet, accessed through your browser (we posted about it recently).
Very shortly I had a rendering of our enneahedron, and I used Sage to confirm that it has all the properties we required. Hooray!
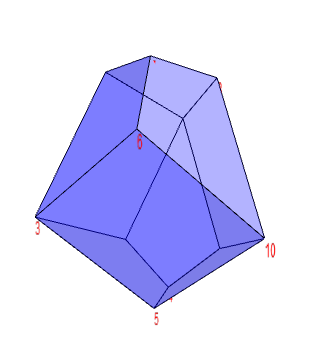
It lives! Sage Cloud’s 3d rendering of our enneahedron.
Invigorated by success, and with confirmation that our measurements fit, I opened up GeoGebra to make a net of the shape. I printed it out, did a bit of cutting and sticking, and voilà: a real life Herschel enneahedron!

I’ve found an animation of the model to show off its groovy shape, since a single photo doesn’t do it justice:
The next step is to see if I can make a poster to educate our students (and staff) about our building’s mathematical namesake. I also think a big sculpture of the Herschel enneahedron would go quite nicely in our school foyer…
More information
The Herschel graph at Wikipedia.
My GeoGebra construction of the polyhedron net.
A LaTeX/TikZ version of the net, ready for printing. John Hammersley of WriteLaTeX kindly made it a template so you can copy it and make your own modifications. For posterity, here’s a locally-hosted PDF of the net.
Andrew Stacey very quickly made his own net by guessing the measurements from the pictures I posted on Google+, and added it to TikZ as a built-in diagram. After a bit of feedback about the angles, he refined it to this finished net, and constructed his own enneahedron.
My construction cam directly from trying to draw the graph in a form that makes the symmetry visible.
Take a trihedral corner with all angles equal (you can chose any angle). Position with the corner pointing up. Intersect it with a vertical equilateral triangular prism turned so its edges are as far from the trihedral edges as possible. This is an end cap.
Make two identical end caps. Turn one upside down, and place the other on top with the 3 outermost points (cut by he corners of the prism) of the two end caps touching. Fill in the four gaps with rhombuses. The shape of the rhombuses will depend on the angle chosen earlier.
The faces of the end caps are planar by construction. The rhombuses, because they connect edges that were all cut by the same a vertical plane.
As a more physically robust alternative to the paper model, I just published a 3D-printable version of the Perfect Herschel enneahedron: http://www.thingiverse.com/thing:248603
Thanks, Bill! A small correction for the description: the graph was named for Alexander Herschel but not created by him.
Fixed in the description. . . but that begs another question: who did create it, and who named it for Herschel? The readily-available (ie. online) sources don’t provide any information about the origin of the graph.
Thank you for the article! I have a question, if I may, regarding the practical side of things… namely, how can we deduce the h=4/3 value without the vector voodoo? While I could deduce the rest (for a square rhombus of side ${A}$, the lower triangle of the kite will be inscribed in a rectangle with sides $\frac{{A}\sqrt{2}}{2}$ respectively $\sqrt{\frac{7}{8}}{A}$) using simple geometry and Pythagoras’s theorem, trying to look into where the kites meet with their upper triangles seems to be quite an ordeal. Maybe I am missing something?
You can also deduce the 4/3 ratio from a projective geometry argument: First, set h1 to 0 and make the polyhedron totally flat. Then, you can see that the kite shaped faces meet to form an equilateral triangle. The proportions of this would dictate that the distance between $v_1$, $v_3$, and $v_{10}$ to the center point, $v_7$, is 4/3 of the distance to the lesser diagonal of the kite. Now, imagine that the polyhedron is reinflated by increasing $h_1$ (and $h_2$). Both $h_1$ and $h_2$ will have to be increased in proportion to the distance from the vertices in order for the kite to stay flat. So, the proportions will stay 4:3 for the line segments I mentioned earlier. Since the kite’s lesser diagonal remains parallel to the plane, it is at height $h_1$. And since the right triangles of height $h_1$ (to the kite diagonal) and $h_2$ (to the top vertex) are proportional, we can say that $h_2$:$h_1$ is in the same 4:3 proportion.
Really cool! I played around a bit with the proportions of the rhombus and found:
1. For your choice of short-diagonal-to-long-diagonal ratio of 1 (a perfect square), the distance from the center of the enneahedron is the same to all points except $v_7$ and $v_4$, which are $\frac{2}{\sqrt{3}}$ further. Following your convention of setting the length of the long diagonal at 1, the volume is $\frac{7 \sqrt{3}}{36}$ and the surface area is $\frac{3+\sqrt{7}}{2}$.
2. To inscribe the enneahedron in a sphere, set the rhombus proportion to $\frac{\sqrt{3}}{2}$. Then the top and bottom vertices $v_7$ and $v_4$ are the same distance from the center as the the three vertices on the equator ($v_1$, $v_3$, and $v_{10}$).
3. Choosing a proportion of $\frac{1}{2}$ makes the angles equal around each point on the diameter (that is, $\angle v_2v_1v_0 \equiv \angle v_2v_1v_8$), which seems visually pleasing.
4. The maximum volume to surface area ratio is achieved with a rhombus proportion of $\sqrt{\frac{9\sqrt{105}-75}{40}}$, which is about 0.6561737.
Thanks! Excellent timing, too – we recently got a 3D printer at work, so of course the first thing I made was a Herschel enneahedron. I’ll print out versions with the parameters you gave.
Minor suggestion – when explaining the properties, you mention “you can’t draw a path on it that visits each vertex exactly once”, but I think it might be more accurate to say “you can’t draw a cycle on it that visits each vertex exactly once”, as there is a Hamiltonian path (I think!). Thanks for the article!
I believe someone (not me) has found an alternative representation of this solid: https://www.shadertoy.com/view/3fKXWG
It’s the intersection of a triangular prism oriented along a cube’s diagonal with that. It looks to have the same topology as your solid and has simpler coordinates (seemingly). I created a Desmos graph: https://www.desmos.com/3d/byicjpr61s
Thanks! I’m not sure that’s the same solid: it looks to me like what should be the middle squares are rectangles in the shadertoy version, so it doesn’t have the same symmetries.