This is part 3 of a three-part series of mathematical speculations about bees. Part 1 looked at honeycomb geometry, and part 2 looked at how bees estimate nest volumes.
The sight of bumblebees roaming around British gardens, foraging for nectar, is common and comforting. The movement of these fuzzy bees between flowers and plants can often seem deliberate yet erratic. Charles Darwin was intrigued by “humble-bee” routines ((Bumblebees were generally known as “humble-bees” until the modern term really caught on in the 1890s.)), and observed them with the assistance of his six children, but always regretted not attaching strands of cotton wool to the bees so he could follow them more easily ((Freeman, Charles Darwin on the Routes of Male Humblebees)).
Within the last decade there has been renewed interest from a number of collaborating researchers into studying bumblebees’ movement between flowers and their foraging techniques. The prevailing journalistic spin on this research seems to be ‘Bees solve the Travelling Salesman Problem – a problem that mathematicians and computers cannot solve’. This is unfortunate, not least because it is gleefully misleading, confusing various meanings of ‘solve’, but also it obscures a lot of the fascinating underlying scientific investigations.
The Travelling Salesman Problem
Imagine a purely mathematical bee: she sets off from her nest with a list of $N$ flowers she must visit before returning home. She wishes to minimise the total length of her flight path between the flowers, so will always fly in straight lines, and never visit the same flower twice in an outing.
Once she has found the flower order that gives the path of minimal distance, she has found the solution to this particular instance of the Travelling Salesman Problem, or TSP (in two-dimensional Euclidean space, which is the only version of the TSP that I’ll mention outside the footnotes).
However, every such mathematical bumblebee must solve a different problem: each has a different list of flowers, with differing numbers of flowers in different locations.
If we were to program robotic bees to pollinate specific flowers efficiently, it would be nice if they could solve the Travelling Salesman Problem in general. That would mean creating an algorithm where, given any list of flowers, the robot always finds the shortest path. It’s conceptually easy to create such a general algorithm: just get the robot to visit the flowers in every possible order, keeping track of the shortest circuit it has found so far. The issue is that this is horribly inefficient, taking $N!$ flights to find the TSP solution for $N$ flowers. Mathematicians don’t know whether there is an algorithm that efficiently solves the TSP in every case. ((There probably isn’t an efficient general algorithm: the 2D Euclidean TSP and wider classes of travelling salesman problems with other metrics, or non-complete graphs are optimisation problems, and they are NP-hard. Informally, it’s hard even to check whether a suggested solution to a particular problem is minimal. These should not be confused with decision problem variants, also confusingly known as travelling salesman problems: find out whether a particular finite graph has a Hamiltonian circuit; does a graph have a Hamiltonian circuit shorter than some given distance $d$. These decision problems are NP-complete, as it’s easy to check whether a proposed solution meets the requirements (ie. in polynomial time). For instance, in the second decision problem you need only to check whether the length of the circuit suggested as a solution is greater or less than the given distance $d$.))
For most purposes, in practice, you don’t need to know how to find the minimal solution efficiently in every case: it’s enough to have strategies or heuristics that help you find approximate solutions that are short and may be close to minimal — for instance, if you looked at each flower in turn and took the minimal distance to any other flower, and summed these lengths up, that would give you a lower bound for the distance of all circuits. So by finding a circuit with a length close to this lower bound, you would know you were even closer to the actual solution. This would be the case with our mathematical bumblebee visiting a list of flowers: the reward in an evolutionary sense is for finding a decent approximate solution without expending too much effort searching. Reducing the distance travelled by that final millimetre to the absolute minimum, while rewarding for mathematicians, doesn’t make much difference to the bees.
How real bees differ
So far we’ve been talking theoretically. Real bees aren’t equipped with lists of flowers they must visit. There’s an extremely wide choice of suitable flowers and bees aren’t restricted in which they can choose. Not all flowers are equal, having all sorts of different properties, such as their colour, scent, and the varying amounts of nectar they produce, as well as changing over time. Bees don’t have perfect knowledge of all flowers or the distances between them, and are quite limited in brain power and memory. Also, bumblebees don’t necessarily fly in straight lines.
Having said all this, we could still reasonably expect that whatever heuristics bees develop or have hard-wired into their brains ((Note the mathematical non-exclusive ‘or’ – bees might be hard-wired to later develop certain heuristic behaviours in some environments.)) to solve their own routing problems might also do quite well at solving the Travelling Salesman Problem. Even if the TSP doesn’t model the bees’ problems in an ideal way, at least the TSP describes a precise problem, and is used in experiments with other animals. Therefore, using the TSP allows comparison of results between species with wildly different environments and behaviours.
Coaxing bees to solve a TSP
So how might you go about designing an experiment to convince bees to follow the rules and solve a Travelling Salesman Problem? For starters, you can restrict the number of flowers available to the bees by performing the experiment in a greenhouse, or in a field otherwise lacking in flowers.
Another strategy is using artificial flowers, to control how much nectar (or rather sugar syrup) each provides. It is good practice here to get an initial baseline measurement of how much a bumblebee’s crop can hold, and then set each of the $N$ artificial flowers to supply $1/N$ of the total nectar the bumblebee requires. This removes variation between flowers, and encourages the bumblebees to visit each flower at least once. As for the problem of bumblebees visiting flowers more than once in a trip, in practice it turns out that usually the bee returns to the most recently visited flower, and these revisits can be ignored.
Finally, we shouldn’t expect the bumblebees to perform well while they are getting used to the layout of the flowers, but we should allow them to perform many foraging flights over the same arrangement to give them a chance to learn.
Bumblebees will often settle upon particular routes between a chosen set of food sources. This behaviour, known as trapline foraging, is shared by other creatures such as hummingbirds, bats, wagtails and capuchin monkeys ((Ohashi, Thomson: Trapline foraging by pollinators: its ontogeny, economics and possible consequences for plants)). If the traplining bee has reliable and renewing sources of nectar, why bother searching for new ones? Visiting in the same order during each foraging flight reduces variation in the time between successive visits, and so the amount of sugary reward is more predictable. Regularly revisiting flowers reduces the benefits received by any competitors interloping onto the bee’s patch. However, the inevitable trade-off is that visiting the same flower too frequently also caps the rewards enjoyed by the foraging bee herself.
Nearest and dearest
A couple of studies approximately following the above design were set up to test whether bees might follow a nearest-neighbour strategy. Following the nearest-neighbour strategy would mean the bees always head next to the closest flower they haven’t yet visited.
The nearest-neighbour strategy is an instance of the greedy algorithm, which means always taking the option at each stage that gives the greatest immediate reward. Specifically, the greedy algorithm involves no planning ahead, and depending on the situation, might not necessarily result in the greatest overall reward. Sometimes it goes completely wrong. In the Euclidean Travelling Salesman Problem, the greedy algorithm typically gets reasonably close to the optimal solution.
As an example of the greedy algorithm, when a UK cashier is handing you back change (1p, 2p, 5p, 10p, 20p, 50p, £1, £2), they can simply choose the largest possible coin not greater than the amount of change needed, subtract it off the total, and do the same with the next. This simple greedy strategy will always result in the smallest possible number of coins handed back.
That the greedy strategy works in this case depends on the values of the coins. The same wouldn’t hold if the cashier were handing back 6p using a selection of historic currency, namely pennies, threepennies (3p) and groats (4p). The greedy strategy here would lead to handing back three coins (4p, 1p, 1p), instead of the optimal two (3p, 3p).
A prime example of where the greedy algorithm fails is the board game Reversi (also marketed as Othello). It’s tempting to be greedy and each turn choose a move that flips over the greatest number of your opponent’s pieces to your own colour. This turns out to be a terrible strategy, especially near the start of the game. You can pit yourself against a silly computer opponent (“Simple Bot”), which uses a version of this strategy.
A greedy approach will fail in many strategy boardgames because human opponents can exploit such a simplistic and predictable strategy, and make short-term sacrifices to improve their long-term position. Equally, if the greedy algorithm is ever optimal, the game won’t be strategic or much fun, and can easily turn into a boring mechanistic chore.
Greedy bees?
Because the greedy nearest-neighbour strategy is simple and works quite well at routing problems, it seems a reasonable hypothesis that bees might use it. However, while flowers aren’t setting out to trick navigating bees, researchers are.
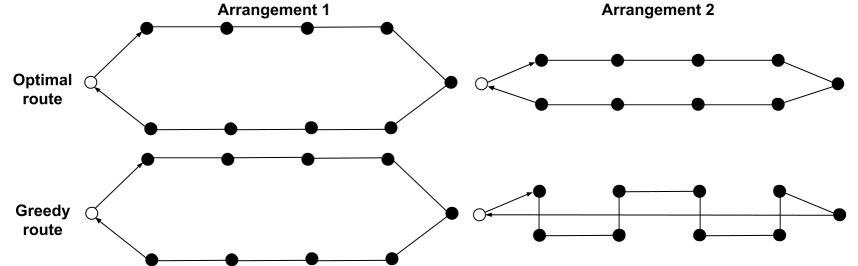
The diagram below depicts two arrangements of artificial flowers (black circles) and two possible routes the bees could decide to take starting and ending at their nest box (white circle). The top row shows the shortest circuit around the flowers, the lower row shows the greedy route a theoretical bumblebee subscribing to the nearest-neighbour strategy would take in each case. In Arrangement 1, the nearest-neighbour route is the shortest. In Arrangement 2, the distance between the two rows of flowers has been decreased so the optimal and greedy routes no longer coincide.
These arrangements were both used in the greenhouse laboratory tests described in the paper “Trapline foraging by bumble bees: IV. Optimization of route geometry in the absence of competition” ((Trapline foraging by bumble bees: IV also tested whether bees might be biased to moving in straight lines – they weren’t.)). The results weren’t conclusive. In Arrangement 1, the bumblebees mostly followed the optimal greedy route. But in Arrangement 2, while the bees didn’t follow the optimal route, they ended up taking a ‘noisy’ variety of suboptimal routes (and not just the greedy one). While this doesn’t point to any particular strategy on the part of the bumblebees, it does suggest that their approach worked well in the arrangement where being greedy paid off, but was more confused when this wasn’t the case.
A later paper, fronted by insect cognition researcher and bee TSP veteran Mathieu Lihoreau, dispels the notion that bumblebees are purely greedy beasts. A flower arrangement was chosen that more severely punished any bees that acted out of strategic greed. Most (6 out of 8) of the bees being tested used the shortest route as their main route (20% of the time), while the other two bees used it as their second most common route. None of the bees used the purely greedy route more often than by chance.
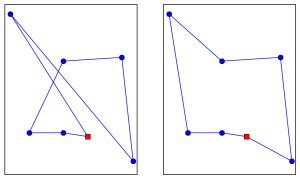
Greedy route (33m, left) and optimal route (24m, right). The red square is the nest box.
One thing that was clear from this set of experiments is that the bumblebees learnt to take shorter routes over time, each continuously reducing the total length of its route over the 80 trips. The picture below shows the paths taken by one of the six bees that took the shortest route more frequently than any other route.
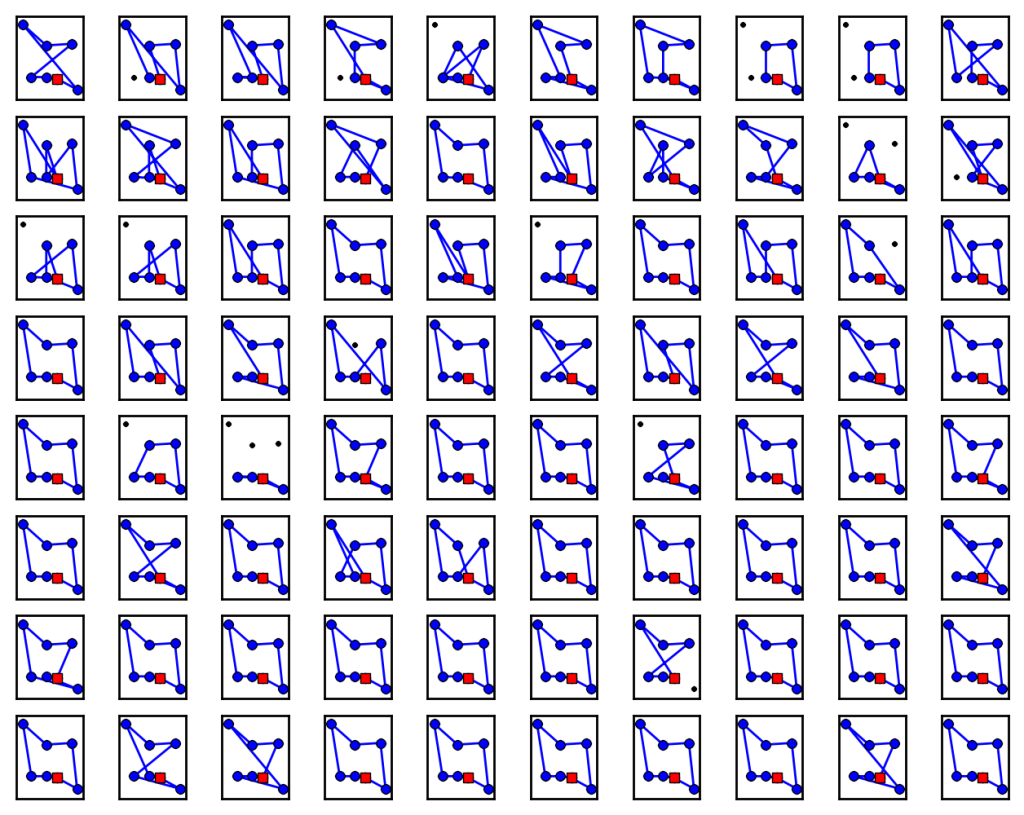
The 80 routes taken by Bee 1 in the experiment, who eventually learnt the optimal route. Unvisited flowers are black dots.
Model behaviour
Lihoreau and two other researchers attempted to mimic the behaviour of bees with computer simulations. Their best attempt led to an algorithm that essentially suggested the bees experiment with different paths between flowers, but prefer hops that had previously lowered the overall distance travelled. The initial probabilities assigned to moving between two flowers in their simulation, the transition probabilities, were inversely proportional to the squared distance between the flowers. This means that the greedy route would initially be the most probable before any learning took place. Each time the bee happens upon a shorter route, all the transition probabilities that went into making up this route are multiplied by a number known as a learning factor (1.1 worked well for them) and then normalised so the probabilities sum to 1. Thus the shortest transitions between flowers start off as the most highly weighted, but when the bee finds a shorter route, the hops between flowers on this route are more likely to be used in future.
Another property of this heuristic is that it is scale invariant: if all the distances between the flowers were multiplied by a constant factor, the model bee would act no differently. Since real bees are going to expend more energy taking suboptimal routes over larger distances, we would expect them to be incentivised to learn more quickly. To account for this, the learning factor can be increased. Increasing the learning factor won’t always lead to improved performance; it simply lowers the amount of risk-taking. If the learning factor is increased too much, the heuristic degenerates into an ‘order of discovery’ rule of thumb, an easy-to-falsify hypothesis that the bees just visit flowers in the order that they discovered them.
Using an increased learning factor of 2, the model did still fit larger scale data collected by Lihoreau and his collaborators when they took the experiments out of the greenhouse laboratory and into a field in Hertfordshire. Attaching tiny radar transmitters to the bumblebees’ backs, the researchers were able to more accurately map out the bumblebee paths. Using radar data, one can depict precise paths between the flowers, dropping the assumptions about direct flights. For instance, initial flights were extremely wiggly, with lengths of about 2000m, while still missing and repeating some of the artificial flowers. Before 30 trips were over though, one bee had optimised its route to 365m, just over the minimum of 312m, visiting flowers in the ideal order and in almost straight lines.
This model, unlike the real bees, will eventually settle permanently on one particular route. Though bumblebees are generally creatures of habit and can be easily tricked into taking suboptimal routes ((Another experiment showed that when the last flower in a learnt optimal circuit was rigged to give more nectar, the bumblebees would sensibly prioritise this highly-rewarding flower, though at the expense of taking a longer route – even though they could have both achieved the same route length and visited the highly-rewarding flower first, by simply flying their original route backwards.)), they do occasionally try out a radically different route, and the converging computer model fails to capture this behaviour. A bee’s thirst for exploration makes sense when faced with a changing environment.
Making beelines
Recreating Lihoreau et al’s algorithm, I’ve generated one possible set of paths that one such simulated bee would take, learning with the same set of flowers as the real bee over the course of 80 foraging trips. At first glance, other than the fact that the simulated bee always visits all the flowers, the paths look quite similar. Both the real and virtual bee visit the optimal route early on, and by the end of the experiment are predominately using it. ((Behold! Using my computer I’ve solved the Travelling Salesman Problem, a problem that even mathematicians with computers are unable to… oh wait, there might be a flaw in the newspaper logic used here.))
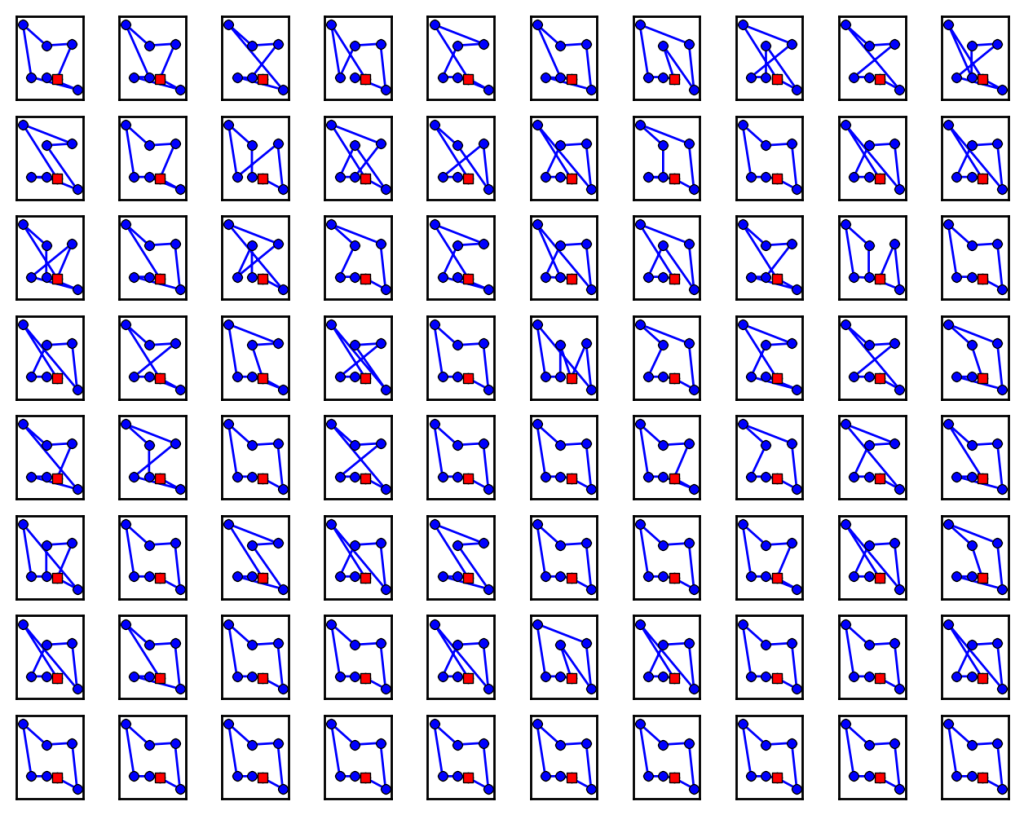
Simulated bee using the probabilistic learning algorithm using a learning factor of 1.2. The greedy path appears frequently in the second-to-last row.
One difference I see is that the simulated bee seems predisposed to use the greedy path more frequently in this flower arrangement than the actual bee. The greedy path only differs here by one ‘choice’ from the clockwise optimal route. You can also observe in these cases that, unlike the computer-generated bee, the real bumblebee is still experimenting with different routes in the final row, even though it’s been using the optimal route more by that point.
It’s easy to find criticisms of any specific algorithm modelling the way bees choose paths between flowers. After all, bee brains are very dissimilar to our mechanical, designed computers and the programs that run on them. But what Lihoreau et al. have shown is that a simple algorithm will adequately capture many aspects of a bumblebee’s behaviour, without attributing any particular sensory or computational superpowers to them. In the end, you could conclude ‘OK, it’s probably not this algorithm that bees are using, but something that feels a bit like it’.
Apiological Part 1: Honeycomb geometry
Apiological Part 2: Estimating nest volumes