 Not content with already having five cubes named after him, internet maths phenomenon James Grime has now developed a new Rubik’s cube-style puzzle for internet maths joy merchants Maths Gear. I’ve been slightly involved in the development process, so I thought I’d share some of the interesting maths behind it.
Not content with already having five cubes named after him, internet maths phenomenon James Grime has now developed a new Rubik’s cube-style puzzle for internet maths joy merchants Maths Gear. I’ve been slightly involved in the development process, so I thought I’d share some of the interesting maths behind it.
Another name for a Rubik’s cube is ‘the Magic Cube’ – and Dr James Grime wondered if you could make a Magic Cube which incorporates its 2D friend, the Magic Square.
Several designs were considered for such a puzzle cube – early ideas included a cube with the numbers 1-54, each face being a normal magic square using the numbers 1-9, with a different multiple of 9 added to give a range for each face. After some searching and testing James settled on one particular type of magic square to make it work.
The Grime Cube is based around the perimeter magic square – an arrangement of the numbers 1-8 such that the three numbers on each edge sum to the same total. For example:

The square above has all four edges adding to 12 (and of course any rotation or reflection of this arrangement will also have this property). One nice interesting maths fact about such constructions is that only six valid perimeter magic squares exist for the numbers 1-8 (obviously, you can just add the same thing to each value to get another one, but that’s not as elegant).
What James Grime discovered was that you could use a Rubik’s cube, where the centres are fixed, to implement a puzzle involving such squares – since the centre of each face is fixed and only the edges move, you could try to arrange the pieces so that they add up to a number given in the centre. There only being six makes this an ideal thing to do on the faces of a cube, and the six squares pair up with each other as complements – so if you overlay two and sum them, the squares in the same place all add to 9.

This nice complement property meant that the cube could be designed to have opposite individual cubies (single chunks of cube) have their faces complement each other – so where there’s a 4 on one face of the cube, the opposite square will be a 5. Dr Grime also worked out a way to arrange six colours on the cube, so that each pair of mini-faces not only sum to 9, but are the same colour – and only one instance of each number/colour (e.g. red 5) occurs anywhere on the cube.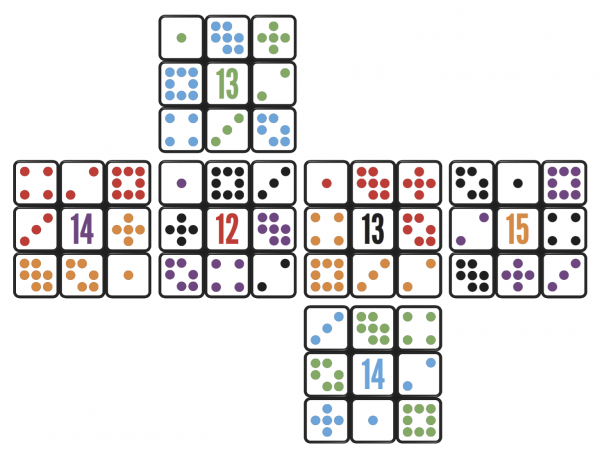

 The final coup de grace for James was discovering a way to arrange the faces on the cube so that these colours could also be solved as a normal Rubik’s cube – an alternative arrangement where each face contains a single colour. This makes it a double puzzle – it can be solved so that either the magic squares work, and the opposite pairs match up, (left) or so that the colours on each face are all the same and there’s still 1-8 on each face (right).
The final coup de grace for James was discovering a way to arrange the faces on the cube so that these colours could also be solved as a normal Rubik’s cube – an alternative arrangement where each face contains a single colour. This makes it a double puzzle – it can be solved so that either the magic squares work, and the opposite pairs match up, (left) or so that the colours on each face are all the same and there’s still 1-8 on each face (right).
As part of the testing process, I’ve had several goes at solving the cube and found it actually pretty pleasing – with my knowledge of how to solve a Rubik’s cube, I know how to put a particular edge or corner piece in a particular place, so I’ve found that very useful. I could find a pair of edge cubies that sit opposite each other (because e.g. the red 4 is always opposite the red 5) and then try other pairs until I get an arrangement that doesn’t use anything disallowed and lets me arrange the rest of the face so the totals are all the same. Then I can figure out which face I’ve just made, arrange it around the right centre face, and start working on the other faces around it. Others may have their own methods but I like how much it makes me think – not just blindly solving the colours, but also having to do sums and deduction along the way.

Grime Cube development montage
There’s another outstanding question about the cube, which Grime doesn’t know a good answer to yet – from the solved-for-magic-squares state, there should be a sequence of moves which translates it to the solved-for-colours state (and the maths tells us that this can be done in fewer than 20 moves, aka God’s Number). So far, James has found a path which takes 70 moves, but who will be the first to find the optimum path?
The Grime Cube is on sale at MathsGear.co.uk for £14.99, and limited stock is available. The last ordering date for delivery before Christmas in the UK is 19th December, and more stock should be available in the New Year.
Is there a typo in the seventh paragraph?
The phrase that puzzles me is the one to the effect that the opposite face of a four will be a four. given the other examples (and the look of the flattened cube), I’d expect that to be four and five.
(I could easily be missing something obvious, and would be glad to be enlightened. Thank you.)
Yes, there was a typo, and I’ve fixed it. Thanks for pointing it out!
Looks like 16 moves is optimal: https://alg.cubing.net/?title=Grime%20CubeColor%20Solution%20toPerimeter%20Magic%20Square&alg=D-_B-_F_R_U2_L-_D2_R-_D-_U_B_L-_R-_D-_B2_R2&view=playback
Such an interesting puzzle, I was wondering about the maths involved with it.
Of course I realized that there would be really interesting topics involved given that this puzzle includes magic squares, rubik’s cubeso, and Dr. James Grimes which are all independently very mathematical.