This week, Katie and Paul are blogging from the Heidelberg Laureate Forum – a week-long maths conference where current young researchers in maths and computer science can meet and hear talks by top-level prize-winning researchers. For more information about the HLF, visit the Heidelberg Laureate Forum website.

The HLF, like all good conference events, has involved a large number of extravagant dinners, serving a variety of delicious food and drink to sustain the high levels of serious mathematical and research conversation. At last night’s Bavarian evening, I noticed a particularly mathematically interesting foodstuff was on the menu, and it’s inspired me enough to write about it.

Alongside the traditional Bavarian wurst and noodles, there was a pile of cooked vegetables, most of which were pretty standard – broccoli, and cauliflower. But in amongst was also a very special type of vegetable – known in German as Pyramidenblumenkohl, or “pyramid cauliflower”, and in English called Romanesco broccoli. In fact, even botanists can’t agree whether it’s really a broccoli or a cauliflower, but everyone who’s ever seen one agrees that it’s beautiful, and mathematically interesting.

Fractal Food

One of the first things you notice when you look at this plant is that it’s made up of a repeated pattern of shapes – each part is a small version of the whole plant, and they get smaller and smaller as you go up to the top.

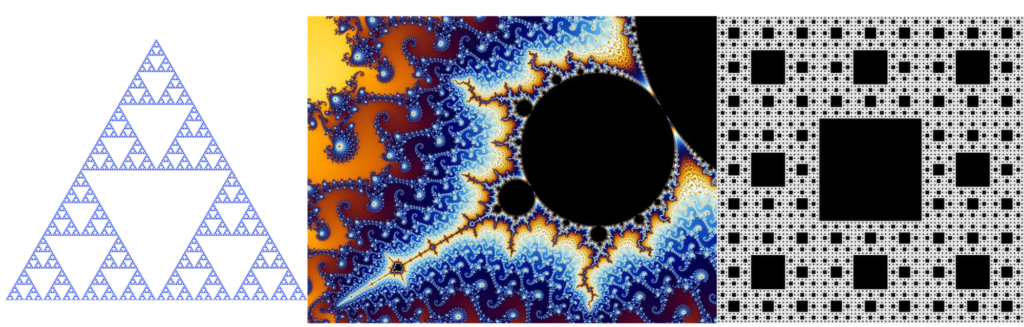
This property of a shape is called self-similarity, and it simply means that small parts of the object have the same structure as the whole shape. This is a property which fractals have, and in fact is one of the defining characteristics of a fractal – if you look at any example of a fractal you should be able to see smaller copies of the shape inside itself, repeated at different sizes all the way down.

In the case of a fractal, this property needs to continue to infinity, and sadly in the case of food it doesn’t carry on forever – but it does mimic the structure of a fractal.

Pre-Spiralised Vegetables

As well as having the excellent fractal property of self-similarity, the Romanesco broccoli also contains a beautiful spiral structure. The spirals go from the tip of each part of the plant and continue around to the base of each floret.

The shape of the spiral is a logarithmic spiral – a spiral whose rate of curving changes along the length of the curve in such a way that the shape of the curve stays the same. So, if you zoom in on a small part of this spiral, it’ll look like the whole curve – it’s also self-similar.

There are many examples of logarithmic spirals in nature, including in nautilus shells, and in the way spiral galaxies form. But this is obviously the most delicious.

But wait, there’s more

Just when you thought you’d discovered all the interesting mathematical properties contained within your dinner – there’s another. If you count the number of spirals running around the florets in each direction, with a small amount of variation due to natural mutations, you’ll find there’s a Fibonacci number of spirals running each way.

The Fibonacci series is a list of numbers dating back to 1202, when Leonardo of Pisa (aka Fibonacci) discovered them as a pattern in various systems. Each Fibonacci number is the sum of the previous two, so if you start with 0 and 1 as the first two numbers, the sequence continues 1, 2, 3, 5, 8, 13, 21, 34, 55 and so on.

The same property of having a Fibonacci number of spirals running in each direction crops up in many other types of plant also – pine cones, pineapples, flower petals and the seeds in sunflower heads have all also exhibited this property – the latter being noted by Alan Turing, and thoroughly researched in a large-scale sunflower growing and observation project that took place in 2012.

Mathematician Vi Hart has produced an excellent series of YouTube videos on the subject, starting with this one.