This week, Katie and Paul are blogging from the Heidelberg Laureate Forum – a week-long maths conference where current young researchers in maths and computer science can meet and hear talks by top-level prize-winning researchers. For more information about the HLF, visit the Heidelberg Laureate Forum website.

Running alongside the 5th HLF is an exhibition of mathematical art by the astrophysicist Aldo Spizzichino. He’s taken ideas from mathematics, and used his own set of programs (in Fortran, no less) to produce his images, a couple of dozen of which are on display in the Old University building a few steps from the forum. Although all the pieces were generating discussion as I looked round the exhibition on Sunday morning, I’ve picked two to talk a bit about, both based on the same piece of maths.

The two pieces are based on Gosper’s curve. It’s a space-filling curve: as more and more iterations are produced, the single line becomes increasingly twisty, in the limit squeezing itself into every point inside its roughly hexagonal fractal boundary.

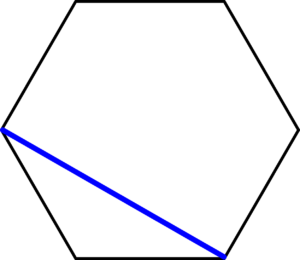
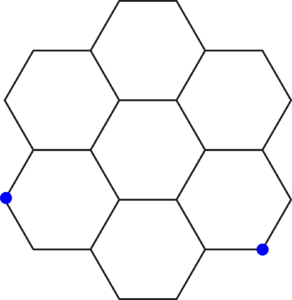
Like all good fractals, the Gosper curve is constructed by a simple process. Start with a regular hexagon, and draw a line on it joining two adjacent-but-one corners (ie, two corners a third of the way round the perimeter from each other). Now make six more of these and arrange the seven ‘tiles’ to form a larger hexagon shape. You can do this so that the lines drawn in the individual hexagons form a single path with its start and end points one-third of the way round the larger shape. I’ve marked the start and end points on the picture below, but not the full path, because I found it a pretty decent puzzle to try and work it out. If you want to know the answer, and see the first few iterations of the curve, you can look at its page on Wolfram Mathworld. Bonus question: is there only one possible path?

Once you have this, you’ve got the basis of a fractal. The large hexagon shape is equivalent to the individual pieces — it can fit together in the same way, and has a path through it with start and end points one-third of the way round the perimeter. So you can repeat the trick: arrange seven of them into the same pattern to form a yet larger hexagon, still with a continuous, but now markedly more intricate, path. And repeat. This process yields the Gosper curve. Since its hexagonal shape resembles a snowflake but it consists of a single line snaking its way round to create the whole figure, it’s also known, brilliantly, as the ‘flowsnake’.

The flowsnake is great, but in some ways it isn’t much to look at. A section from the middle looks basically indistinguishable from any other (I guess that’s kind of the point of a fractal). A lot of the interest is in the boundary of the curve, which gets increasingly more complex as the iterations continue. The pieces on display in Math ⇔ Art cleverly use different transformations to add interest to the presentation and shine new light on the curve.

One of them, ‘Moonlight’ (below), uses a polar transformation, creating a point along the boundary where the white curve is so densely packed to appear as a bright ‘moonrise’. In my favourite of the two, “Zigzag Path to a Fractal Island”, Spizzichino uses circular inversion to ‘flip’ the fractal, so the curve surrounds its boundary, the empty ‘outside world’ appearing as the island of the title. He describes this as a “kind of ‘Neverland,’ towards which the Gosper’s flake converges, but never reaches”. The distortion applied to the curve means that it’s visible at different scales at the same time, reflecting the iterative process that it arises from.