If you are like me, you have played the game SET and have probably been perplexed at how quickly some people can play the game! Even as the game is quite easy to explain, it takes some time to build various strategies and pattern recognition to play the game effectively. If you have never heard of SET, don’t fret because we will soon review its layout. For my final masters project at Texas A&M University, we had the autonomy to research any higher-level mathematical topic and I felt SET would be a great venue to tap into some deeper mathematics. Little did I know how truly complex and elegant SET really is with connections to combinatorial geometry, finite affine geometry, and vector spaces over finite fields, some of these problems still open in research-level mathematics. All of these topics (and more) are included in a great resource I highly recommend for some summer reading. Check out The Joy of Set by McMahon, et al. to dig deeper into what is presented below.
What is SET?
Although we know it is a fun family game, SET originated as a pictorial model of representing different gene expressions of epileptic German Shepherd dogs. Invented in 1974, Marsha Falco used different attributes of cards to try to create a visual representation of different types of genes. The game was finally marketed in 1990 as the game we now know. So how exactly are the cards designed in the game?
Any given card in the SET deck has one of four attributes (number, color, shading, shape) and there is only one such card with each combination. And each attribute has one of three values. Consider the table below that lists the attributes available and their associated values:
| Attribute | Value | Coordinate |
|---|---|---|
| Number | $3$, $1$, $2$ | $0$, $1$, $2$ |
| Color | Green, Purple, Red | $0$, $1$, $2$ |
| Shading | Plain, Striped, Solid | $0$, $1$, $2$ |
| Shape | Diamond, Oval, Squiggle | $0$, $1$, $2$ |
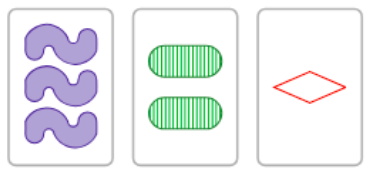
For instance, the card shown below consists of three green plain ovals. Arbitrarily, we can coordinatize the cards based on the value of each attribute. Thus, instead, this card could be thought of as the vector $(0,0,0,1)$. More soon on how we can use vector spaces to analyze the game of SET!
The entire goal of the game is to layout twelve initial cards from a well-shuffled deck and yell out “SET!” when a SET is found. So what is a SET then? A SET is a collection of three cards such that for each of the four attributes, the cards are all the same or all different values. In the picture below, one such set is comprised of the $1$ green striped diamond, $2$ green plain ovals, and $3$ green shaded squiggles. Or in terms of vector coordinates, $(1, 0, 1, 0)$, $(2, 0, 0, 1)$, and $(0, 0, 2, 2)$. Note that across the four attributes, color is the only alike attribute so we often call this a $1$-alike SET. Can you find a $2$-alike SET in the picture below? Are there any others? How do you know for sure?
Affine Geometry
It turns out that the entire SET deck represents a finite affine geometry which we call $\text{AG}(4,3)$. The “$4$” represents four-dimensional space and the “$3$” means that there are three points per line. Affine geometry contains only a few axioms whose central notion is to emphasize the idea of parallel lines without the overhead of a metric for distance or angle measure such as in Euclidean Geometry. Here are axioms of affine planar geometry:
- There exist at least three non-collinear points.
- Each line contains at least two points.
- Two points determine exactly one line.
- Given any line $\ell$ and any point $P$ not on $\ell$, there is exactly one line $m$ containing $P$ where $\ell \cap m = \varnothing$.
In this scheme, every SET card is a point and every SET is a line. Note the third axiom tells us that two cards uniquely determine a SET since the third card would be determined. Sometimes SET aficionados call this the fundamental theorem of SET.
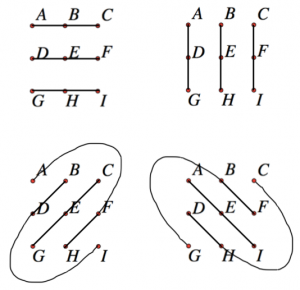
So what exactly is a plane, denoted $\text{AG}(2,3)$, or even a hyperplane, $\text{AG}(3,3)$? A plane can be visualized as follows consisting of 12 lines which can be partitioned into four parallel classes:
Equivalently, we can think of forming lines by tiling with the plane of nine points and looking for any three collinear points to form a line:
Combinatorics and Probability
Before you directly count the total number of cards in your SET deck, see if you can calculate how many cards such a deck contains. Using the Fundamental Counting Principle, we can see that since each attribute has three possible values and there are four independent attributes, there are $3^4=81$ possible cards. Since no card is repeated in the deck, there must be $81$ cards (or points). So how many SETs (or lines) are there in a deck of $81$ cards? One way to count this is to employ our fundamental theorem and just analyze $2$ cards since the third will be determined. There are $81\times 80$ ways to select the two distinct cards that uniquely determines a SET; however, once the three cards are selected, we can permute them in $3!$ ways resulting in $\frac{81 \cdot 80}{3!}=1080$ total SETs. Equivalently, by dividing numerator and denominator by $2$, we have $\frac{81 \cdot 40}{3}$ showing that given a card, there are $40$ such pairs of the remaining $80$ cards that make a SET with that given card.
Now that we have SETs counted, let’s try to partition these SETs into $0$-alike, $1$-alike, $2$-alike, and $3$-alike SETs. Note there are no $4$-alike SETs (why?). The table below shows these counts and the reader should verify that the sum is $1080$ as we found before. Nicely enough, this count shows that $3$-alike SETs are the most rare, though, psychologically they seem far easier to find than their $0$-alike counterparts.
| Type | Count | Probability |
|---|---|---|
| $0$-alike | $\frac{81\cdot {4 \choose 0}\cdot 1^0 \cdot 2^4}{3!}=216$ | $20\%$ |
| $1$-alike | $\frac{81\cdot {4 \choose 1}\cdot 1^1 \cdot 2^3}{3!}=432$ | $40\%$ |
| $2$-alike | $\frac{81\cdot {4 \choose 2}\cdot 1^2 \cdot 2^2}{3!}=324$ | $30\%$ |
| $3$-alike | $\frac{81\cdot {4 \choose 3}\cdot 1^3 \cdot 2^1}{3!}=108$ | $10\%$ |
We can count the number of planes by recognizing that three non-collinear points form a unique plane. The reader is encouraged to start with any $3$ such points, such as those in the configuration below, and continue to complete SETs. You should find that you are limited to only nine cards. Through this configuration, there are then $\frac{81\cdot 80 \cdot 78}{9 \cdot 8 \cdot 6}=1170$ total planes in the SET deck! Plane and simple. In a similar way, we can see that there are $\frac{81 \cdot 80 \cdot 78 \cdot 72}{27 \cdot 26 \cdot 24 \cdot 18}=120$ total hyperplanes.
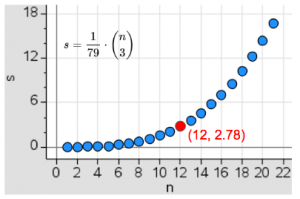
How many SETs can we expect in an initial layout of $12$ cards? Since the probability of any three cards making a SET is $\frac{1}{79}$, linearity of expected value allows us to expect ${12 \choose 3}\cdot \frac{1}{79}\approx 2.79$ SETs in an initial layout of $12$ cards. The graph below shows (as expected) that the expected number of SETs increases as the number of cards $n$ in the layout increases.
I wrote some Java code to simulate the game and found that this expected value agreed with looking at the number of SETs among the initial $12$ cards across one million trials. Curiously though, the simulation showed that the probability of the initial layout not containing a SET is $\approx 3.23 \%$, slightly different than the advertised probability on the SET box, $33:1 \approx 2.94\%$… Further, a related simulation played out the entire game by collecting all the available SETs in an ArrayList and selecting one SET at random to remove from the layout. Note that if no SET is available in the layout, $3$ more cards are dealt. If there are $12$ cards on the table when a SET is taken, then $3$ more cards are dealt, otherwise, a SET is taken without adding more cards to the layout. The table below shows the number of cards left at the end of a game for one million trials. Do you notice anything curious?
| Cards Left | Probability |
|---|---|
| $0$ | $1.22\%$ |
| $3$ | $0%$ |
| $6$ | $46.81\%$ |
| $9$ | $44.55\%$ |
| $12$ | $7.35\%$ |
| $15$ | $0.079\%$ |
| $18$ | $0.0001\%$ |
| $21$ | $0\%$ |
You might see that while $0$ cards left in a full SET game is especially rare, it is nowhere close to the probability of having $18$ cards left with no SET. But is it really the case that $3$ cards or $21$ cards cannot be leftover? In other words, must these “final” collections contain a SET? Why?
Vector Spaces over Finite Fields
As alluded to earlier, we can think of the SET deck as a vector space where each vector has four components over $\mathbb{F}_3$, the finite field with $3$ elements, isomorphic to $\mathbb{Z}/3\mathbb{Z}$. Since these vectors are ordered $4$-tuples, we can write this vector space as $\mathbb{F}_3^4$. Under this scheme, three cards make a SET if and only if their vector sum (component-wise) is $\overrightarrow{0}$. Note that $0+0+0=1+1+1=2+2+2=0+1+2\equiv 0 (\bmod 3)$, showing the forward implication. And one can directly check that all $3^3$ possibilities show that $a+b+c\equiv 0 (\bmod 3)$ precisely when either $a=b=c$ or $a=0$, $b=1$, $c=2$ in some order. This rule (sometimes called the Affine Collinearity Rule) now shows why it is impossible to have $3$ final cards leftover in a game of SET. Since we can partition an initial full deck of $81$ cards into $27$ SETs, the vector sum of all the cards in the deck is $\overrightarrow{0}$. As the game plays on by taking SETs, this vector sum continues to be $\overrightarrow{0}$, an invariant during the game. Thus, if three cards remain at the end of the game, their vector sum too is zero showing they must form a SET!
We can also apply the Affine Collinearity Rule to the last six cards of a SET game. Let these cards be denoted $A, B, C, D, E, F$. Without loss of generality, pair up the cards as follows: $\{A, B\}, \{C, D\}, \{E, F\}$ where $A+B+C+D+E+F=\overrightarrow{0}$ since they are the remaining cards in the game. We now show the remaining cards, say $X, Y, Z$ that will form a SET with each pair will form a SET themselves. Since three new SETs are formed, $\overrightarrow{0}=(A+B+X)+(C+D+Y)+(E+F+Z)$ and by associativity, $\overrightarrow{0}=(A+B+C+D+E+F)+(X+Y+Z)$. By substituting, we find $(X+Y+Z)=\overrightarrow{0}$. Vectors for the win!
An especially cool connection to Euclidean geometry is using vectors to quickly find the third card that will make a set with two given cards. Looking componentwise, given an attribute with values $a, b \in \mathbb{F}_3$ for the given two cards, we wish to find $c \in \mathbb{F}_3$ such that $a+b+c \equiv 0(\bmod 3)$. Then $c \equiv -a – b (\bmod 3) \equiv -(a+b) (\bmod 3)$. But since $-1\equiv 2 (\bmod 3)$ and $2^{-1} = 2$ in $\mathbb{F}_3$ under multiplication, this shows $c \equiv \frac{a+b}{2}(\bmod 3)$. In other words, $c$ is the midpoint of $a$ and $b$. In this sense, any one of three points on a line is the midpoint of the other two!
We now can recast Axiom AG$4$ differently by vector translation: Given set $S = \{v_1,v_2,v_3\}$ and $w \notin S$, then there exists a unique set $T$ such that $w \in T$ and $S||T$. In particular, we can let $\{v_1+\alpha, v_2+\alpha, v_3 + \alpha\}$ denote this new set $T$ for any vector $\alpha$. The reader is encouraged to show that by letting $\alpha = w – v_i$ for one such $i$, the set $T$ is the same regardless of the choice of $i = 1, 2, 3$. Now we can show that two non-intersecting SETs are parallel if and only if there exists a plane that contains both SETs. Similarly, planes and hyperplanes can be defined via vector addition.
In particular, we define an affine transformation as some $T(v) = Mv + b$ where $M$ is a nonsingular $4 \times 4$ matrix with entries from $\mathbb{F}_3$ and $b \in \mathbb{F}_3^4$. Such transformations send lines to lines (and further, planes to planes, etc.). That is, if $S=\{v_1, v_2, v_3\}$ is a SET, then we wish to show $T(S)=\{T(v_1), T(v_2), T(v_3)\}$ is also a SET. Note that $T(v_1) + T(v_2) + T(v_3) = (Mv_1+b)+(Mv_2+b)+(Mv_3+b)$ and by associativity, this equals $M(v_1+v_2+v_3)+3b = M(\overrightarrow{0})+\overrightarrow{0} = \overrightarrow{0}$ showing that $T(S)$ is also a SET. Such an affine transformation is completely determined by its action on 5 points said to be in free position, namely, no 3 are collinear, no 4 are coplanar, and no 5 are cohyperplanar. Can you find an example of 5 such points? How many total affine transformations are there?
Maximal Caps
If you haven’t been convinced yet of the rich mathematics embedded in SET, perhaps fields medalist Terry Tao can convince you otherwise. In his blog in 2007, he wrote, “Perhaps my favourite open question is the problem on the maximal size of a cap set“. What is a cap set you ask?
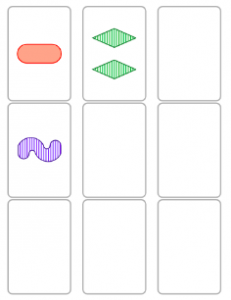
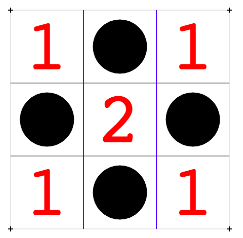
In $\text{AG}(n,3)$, a collection of points (or cards) with no lines (SETs) such that no 3 points are collinear is known as a cap. A cap is complete if adding any other point from that space will form a line. A cap is maximal if it is complete and of largest size. Using Jordan Awan’s CapBuilder site, we can easily find that the maximal cap of dimension 2 (a plane) is only 4 cards, as shown below. Note that such a max cap is formed by removing the intersection point of two lines, indicated by the “$2$” in the diagram, meaning that two lines would be formed by the introduction of that point to the collection. Such a configuration of points is called an interset among SET nerds since it is the intersection of SETs.
Moving to higher dimensions, the max caps problem gets intractable really fast. In $1947$, Bose proved that the max cap for dimension $3$ is $9$ points and it wasn’t until $1970$ that Pellegrino showed that it is $20$ for one dimension higher. In $\text{AG}(2,3)$ every complete cap is maximal, but in $\text{AG}(3,3)$ not all complete caps are maximal, such as those consisting of just $8$ points. The reader is encouraged to try to find one such complete, non-maximal cap for dimension $3$. Since the maximal cap of $\text{AG}(3,3)$ is $20$, it is now clear why $21$ cards must have contained a SET in our earlier simulation! In fact, such a configuration of $20$ cards is the intersection of $10$ lines with the common intersection point (or anchor point) removed. In 2002, Edel et al. showed that for dimension $5$ the max cap is $45$ points and recently in $2008$, Potechin showed that the max cap for dimension $6$ is $112$ points. No one knows the max cap for higher dimensions…
Generalizations
If you are into combinatorics, consider a new SET game consisting of $n$ attributes with $3$ types per attribute. Usual SET is played with $n = 4$. Now there are $3^n$ points and $\frac{3^n \cdot (3^n-1)}{2} \cdot \frac{1}{3}$ = $\frac{3^{n-1}(3^n-1)}{2}$ lines. If we let $g(n,k)$ denote the number of SETs with $k$-alike attributes, what is the value $g(n,k)$? Consider a vector $v = (x_1,x_2,…,x_n)\in \mathbb{F}_3^n$.
We can choose the $k$-alike components in $n \choose k$ ways. We can choose the values of the $k$-alike components of each vector in $3^k$ ways. This leaves $n-k$ remaining attributes which we can assign $\{0, 1, 2\}$ in $3! = 6$ ways to the three cards resulting in $6^{n-k}$ ways, but we must divide by $3!$ to undo rearrangement of the three cards. By independence, there are then ${n \choose k}3^k \cdot 6^{n – k -1} = {n \choose k}3^{n-1}2^{n – k – 1}$ $k$-alike SETs. As was the case with $n= 4$, we can show that the sum of these counts is the total number of SETs. Using the Binomial Expansion Theorem, $3^n = \sum_{k = 0}^n {n \choose k} 2^{n – k}$. Subtracting the last term, $1$, from both sides, $3^n -1 = \sum_{k = 0}^{n-1} {n \choose k} 2^{n – k}$. Thus, $\frac{3^{n-1}(3^n-1)}{2} = \sum_{k = 0}^{n-1} {n \choose k}3^{n-1} 2^{n – k-1}$, where the righthand side is simply the sum of all $g(n,k)$.
Similar to as we counted before, there are $\displaystyle \frac{3^n(3^n-1)(3^n-3)\dots(3^n – 3^{k-1})}{3^k(3^k-1)(3^k-3)\dots(3^k – 3^{k-1})}$ such $k$-dimensional hyperplanes. Consider a bipartite graph mapping cards to $k$-dimensional hyperplanes. Each of the $3^n$ cards belongs to $x$ such hyperplanes and any one hyperplane is comprised of $3^k$ cards. Thus, using an incidence count, we have $x\cdot 3^n = g(n,k)\cdot 3^k$ and by substitution,$x = \displaystyle \frac{(3^n-1)(3^n-3)\dots(3^n – 3^{k-1})}{(3^k-1)(3^k-3)\dots(3^k – 3^{k-1})}$, representing the number of $k$-dimensional hyperplanes through a given card. Such a quantity is sometimes referred to as a $3$-binomial coefficient, written as $\left[ \matrix{n \\ k} \right]_3$. Generally, $\left[ \matrix {n \\ k}\right] _q = \frac{(q^n-1)(q^n-q)\dots(q^n – q^{k-1})}{(q^k-1)(q^k-q)\dots(q^k – q^{k-1})}$ is a $q$-binomial coefficient, which counts the number of subspaces of an $n$-dimensional vector space over finite field $\mathbb{F}_q$. In fact, one can show via L’Hopital’s Rule that $\left[ \matrix{n \\ k} \right] _q \rightarrow \left( \matrix{n \\ k} \right) $ as $q \rightarrow 1$. Now that’s cool!
Summary
It is my hope that this post has given you some insight into the deep and elegant complexities of the game of SET besides just trying to be the fastest SET-finder in a game. It is miraculous that such a simple game can have such beautiful and joyful connections to some advanced domains of mathematics, even with some open research questions. If interested, the reader is encouraged to explore some of these considerations or generalizations, either playing with finite geometry or doing some combinatorics. The SET community has also developed some other very interesting variations on SET and their connections to other geometries, such as projective geometry, known as ProSet.
Note: Special thanks goes to Gwyneth Whieldon who put together typeset SET cards. Also, special thanks goes to my TAMU masters committee (thanks Jenn, Frank, and Mary!).



A fun twist on the end of a game of set: https://jeremykun.com/2018/03/25/a-parlor-trick-for-set/