I made this. Here’s how…
Rob Eastaway tweeted a little curiosity he had been given by Tim Rowett – an equation that works as an equation when rotated 180°.
To make this isn’t completely trivial. It seems clear that $x$, $1$ and $8$ have rotational symmetry, such that they work either way up (you may have to draw an unusually symmetric $8$). The same is true of $+$, $-$, implicit multiplication and the horizontal line in a fraction. It is also clear that some numbers have no rotational symmetry and so cannot be used. A $2$, $3$, $4$ or $7$, no matter how you draw it, won’t look like anything useful when rotated. If you draw them right, a $6$ and a $9$ can be rotations of each other. This leaves $5$. As far as I am concerned, if you draw it in a certain way it is recognisable when rotated (as in the tweet at the top of this post).
You also have to consider the order of operations and ensure this makes sense both ways up. For example, you can’t start one side of the equation like $-1+\ldots$, because when rotated this would look like the nonsensical $\ldots+1-$. By careful use of symbols, you can make equations that are valid and soluble when rotated.
So far, so curious. But Rob posed an interesting question: does a similar equation exist that has the same solution both ways?
I realised that the arrangement of fractions in the equation Tim gave Rob were leading to one solution one way up and two solutions the other way up, meaning there was no possibility of a complete match. So I wondered if it might be possible to find a set of four constants with appropriate values for which one solution matched.
That is, we want equations of the form
\[ \frac{x}{a}=b-\frac{c-x}{d}\text{.} \]
with $a,b,c,d \in \{1,5,6,8,9\}$, for which one solution of the rotated equation matches the solution of the non-rotated equation.
Say the rotated form is
\[ \frac{e}{x-f}-g=\frac{h}{x}\text{.} \]
Such that $d$ rotates to give $e$ using the following mapping:
\[\begin{align*} 1 &\to 1;\\ 5 &\to 5;\\ 6 &\to 9;\\ 8 &\to 8;\\ 9 &\to 9. \end{align*} \]
And $c$, $b$ and $a$ map to $f$, $g$ and $h$, respectively, using the same mapping.
First, we solve the non-rotated version of the equation in general form:
\[ \begin{align*} \frac{x}{a} &= b-\frac{c-x}{d}\\ \frac{x}{a} – \frac{x}{d} &= b-\frac{c}{d}\\ x \frac{d-a}{da} &= \frac{bd-c}{d}\\ x &= \frac{abd-ac}{d-a}\text{.} \end{align*} \]
Then we solve the rotated version:
\[ \begin{align*} \frac{e}{x-f}-g&=\frac{h}{x}\\ ex – gx(x-f) &= h(x-f)\\ 0 &= gx^2 + (h-e-fg)x – hf \end{align*} \]
So, applying the quadratic formula,
\[ x = \frac{(fg+e-h) \pm \sqrt{(h-e-fg)^2 + 4fgh}}{2g}\text{.} \]
I wrote a little Python 3 program to exhaustively search, testing each of the possible values of $a$, $b$, $c$ and $d$ to see if we had a match.
Here is my rotate(n) function, which take a number n and returns its rotated version.
def rotate(n):
if n==1 or n==5 or n==8:
return n
elif n==6:
return 9
elif n==9:
return 6
else:
raise ValueError("Input should be 1, 5, 6, 8 or 9")
And here is the code for running the search. It uses SciPy for the square root to deal with any potential complex numbers.
import scipy as sp
candidatevalues = (1,5,6,8,9)
for a in candidatevalues:
for b in candidatevalues:
for c in candidatevalues:
for d in candidatevalues:
if d!=a and a!=1 and d!=1: # mustn't divide by zero! Also a and d !=1 so not trivially reducible
e = rotate(d)
f = rotate(c)
g = rotate(b)
h = rotate(a)
x1 = (a*b*d - a*c) / (d-a) # solution a,b,c,d
x2 = ( (f*g+e-h) + sp.sqrt( (h-e-f*g)**2 + 4*f*g*h ) )/(2*g) # +ve solution e,f,g,h
x3 = ( (f*g+e-h) - sp.sqrt( (h-e-f*g)**2 + 4*f*g*h ) )/(2*g) # -ve solution e,f,g,h
if x1==x2 or x1==x3:
print(a,b,c,d," / ",e,f,g,h," / ",x1,x2,x3)
This method found three solutions.
I figure you could set up a neat trick where you say “solve this equation” (the $a$, $b$, $c$, $d$ version), “then rotate the equation 180° and input your value for $x$”. Because the solution to the non-rotated equation is one of the solutions to the rotated one, the player would find their answer works both ways up. Astonishment, fame and riches naturally follow!
But it isn’t completely satisfying, is it?
Playing around on paper, I came up with an equation format that would yield two solutions in either case and ran a similar piece of code. This found eight non-trivial equations that had the same pair of solutions either way. Really, this is four pairs of equations, where each pair are a trivial rearrangement of the each other.
| Non-rotated | Rotated | Solutions |
|---|---|---|
| $\frac{x-1}{6}=\frac{9}{5-x}$ | $\frac{x-5}{6}=\frac{9}{1-x}$ | $x=3 \pm 5\mathrm{i}\sqrt{2}$ |
| $\frac{x-1}{9}=\frac{6}{5-x}$ | $\frac{x-5}{9}=\frac{6}{1-x}$ | $x = 3 \pm 5\mathrm{i}\sqrt{2}$ |
| $\frac{x-1}{6}=\frac{9}{8-x}$ | $\frac{x-8}{6}=\frac{9}{1-x}$ | $x = \frac{9\pm\mathrm{i}\sqrt{167}}{2}$ |
| $\frac{x-1}{9}=\frac{6}{8-x}$ | $\frac{x-8}{9}=\frac{6}{1-x}$ | $x = \frac{9\pm\mathrm{i}\sqrt{167}}{2}$ |
| $\frac{x-5}{6}=\frac{9}{8-x}$ | $\frac{x-8}{6}=\frac{9}{5-x}$ | $x = \frac{13 \pm 3\mathrm{i}\sqrt{23}}{2}$ |
| $\frac{x-5}{9}=\frac{6}{8-x}$ | $\frac{x-8}{9}=\frac{6}{5-x}$ | $x = \frac{13 \pm 3\mathrm{i}\sqrt{23}}{2}$ |
| $\frac{x-6}{5}=\frac{8}{9-x}$ | $\frac{x-6}{8}=\frac{5}{9-x}$ | $x = \frac{15 \pm \mathrm{i}\sqrt{151}}{2}$ |
| $\frac{x-9}{5}=\frac{8}{6-x}$ | $\frac{x-9}{8}=\frac{5}{6-x}$ | $x = \frac{15 \pm \mathrm{i}\sqrt{151}}{2}$ |
So far, so good, but the solutions were all complex. In some ways, complex number solutions are fine. But, really, it’d be nicer and more accessible as a trick to have real solutions.
Finally, I did a bit of tweaking to try to increase the chances the discriminant was positive, essentially by changing the minuses to pluses, and found some with real solutions.
| Non-rotated | Rotated | Solutions (2 d.p.) |
|---|---|---|
| $\frac{x+1}{6}=\frac{9}{5+x}$ | $\frac{x+5}{6}=\frac{9}{1+x}$ | $4.62,-10.62$ |
| $\frac{x+1}{9}=\frac{6}{5+x}$ | $\frac{x+5}{9}=\frac{6}{1+x}$ | $4.62,-10.62$ |
| $\frac{x+1}{6}=\frac{9}{8+x}$ | $\frac{x+8}{6}=\frac{9}{1+x}$ | $3.64,-12.64$ |
| $\frac{x+1}{9}=\frac{6}{8+x}$ | $\frac{x+8}{9}=\frac{6}{1+x}$ | $3.64,-12.64$ |
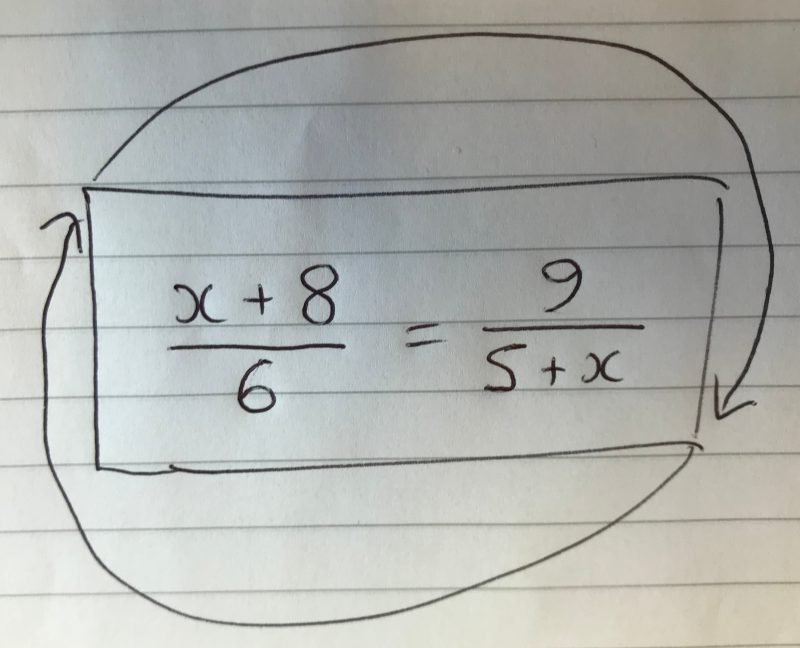
| $\frac{x+5}{6}=\frac{9}{8+x}$ | $\frac{x+8}{6}=\frac{9}{5+x}$ | $1,-14$ |
| $\frac{x+5}{9}=\frac{6}{8+x}$ | $\frac{x+8}{9}=\frac{6}{5+x}$ | $1,-14$ |
| $\frac{x+6}{5}=\frac{8}{9+x}$ | $\frac{x+6}{8}=\frac{5}{9+x}$ | $-1,-14$ |
| $\frac{x+9}{5}=\frac{8}{6+x}$ | $\frac{x+9}{8}=\frac{5}{6+x}$ | $-1,-14$ |
From these, I picked one with integer solutions which I found fairly pleasing symmetrically, and tweeted it.
I’m sure there will be other equation formats out there that yield solutions with this property, but that’ll do for me. Here’s the full code that found the eight real solutions.
# non-rotated: (x+a)/b = c/(d+x)
# rotated: (x+e)/f = g/(h+x)
import scipy as sp
def rotate(n):
if n==1 or n==5 or n==8:
return n
elif n==6:
return 9
elif n==9:
return 6
else:
raise ValueError("Number should be 1, 5, 6, 8 or 9")
candidatevalues = (1,5,6,8,9)
for a in candidatevalues:
for b in candidatevalues:
for c in candidatevalues:
for d in candidatevalues:
e = rotate(d)
f = rotate(c)
g = rotate(b)
h = rotate(a)
if (not (a==h and b==g and c==f and d==e)) and (not (a==e and b==f and c==g and d==h)) and b!=1 and c!=1: # only test cases that aren't boring and b and c !=1 so not reducible
x1 = (-(d+a) + sp.sqrt((d+a)**2 - 4*(a*d-b*c)))/2 # a,b,c,d +ve
x2 = (-(d+a) - sp.sqrt((d+a)**2 - 4*(a*d-b*c)))/2 # a,b,c,d -ve
x3 = (-(h+e) + sp.sqrt((h+e)**2 - 4*(e*h-f*g)))/2 # e,f,g,h +ve
x4 = (-(h+e) - sp.sqrt((h+e)**2 - 4*(e*h-g*f)))/2 # e,f,g,h -ve
if (x1==x3 and x2==x4) or (x1==x4 and x2==x3):
print(a,b,c,d," / ",e,f,g,h,"/",x1,x2)
Well, calculator-style 2 looks like 2 when rotated.
Yes, I suppose so. It is a trivial change to the code to allow and search for 2 also as its own rotation. Doing so finds another 10 equations in this format with real solutions. So if you are happy to typeset in a calculator font, you can make equations from the following:
For example, the third of these (2 6 9 5) yields:
\[ \frac{x+2}{6} = \frac{9}{5+x} \]
and reversed (5 6 9 2):
\[ \frac{x+5}{6} = \frac{9}{2+x} \text{,} \]
both of which have solutions $(4,-11)$.
It is not immediately obvious to me that the program will not lose some solutions due to floating point precision errors. I do not think anything bad could happen in this particular case, but it is something you have to be careful about in general when writing programs like this. I would rather write the test as (d+a) == (h+e) and (d+a)**2 – 4*(a*d-b*c) == (h+e)**2 – 4*(e*h-f*g) (or use a symbolic computation library) — this should be safe.
What one really wants is rotated equations with the same solutions where one is very easy to solve and the other very difficult. Then you challenge your friend and your enemy to solve them fastest, but rotate the question for your enemy. Your friend announces the solution very quickly, your enemy checks it works and credits your friend with great mathematical powers.