This is the fourth match in our group stage: from Group 4, it’s Colin Beveridge against Kyle D Evans. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Colin Beveridge – Left as an Exercise: The Sagrada Família

Colin Beveridge is an author of popular maths books. He writes the Flying Colours Maths blog, brings up two children with his partner, and has his eyes on a triathlon in the distant future. He’s @icecolbeveridge on Twitter.
The Sagrada Família is an enormous, unfinished basilica in Barcelona, generally recognised as architect Antoni Gaudí’s masterpiece. It’s also full of maths – this video barely scratches the surface.
Links:
- Official website
- Wikipedia
- The magic square
- The geometry of Gaudí
- The geometry of the Sagrada Família
- Arches and ruled surfaces
- Art and mathematics in the Sagrada Família
Kyle D Evans –

Kyle D Evans is an award-winning maths communicator, musical comedian, teacher and general jack of all mathematical trades. He’s @kyledevans on Twitter.
I’m a big fan of fractals – I find them endlessly fascinating. Wikipedia describes a fractal as: “a subset of a Euclidean space for which the Hausdorff dimension strictly exceeds the topological dimension”, but I promised to write these pieces so that normal people could understand them, so we’ll describe a fractal as any shape that exhibits self-similarity. If you already know a lot about fractals, I make no apology – I find them endlessly fascinating. Wikipedia describes them as….
A beautiful example of a fractal is the Koch snowflake (teachers – your students might like to try constructing these with compasses. And some advice: Koch is pronounced either ‘cotch’ or ‘coke’, depending on who you ask, so no risk of classroom sniggering either way):
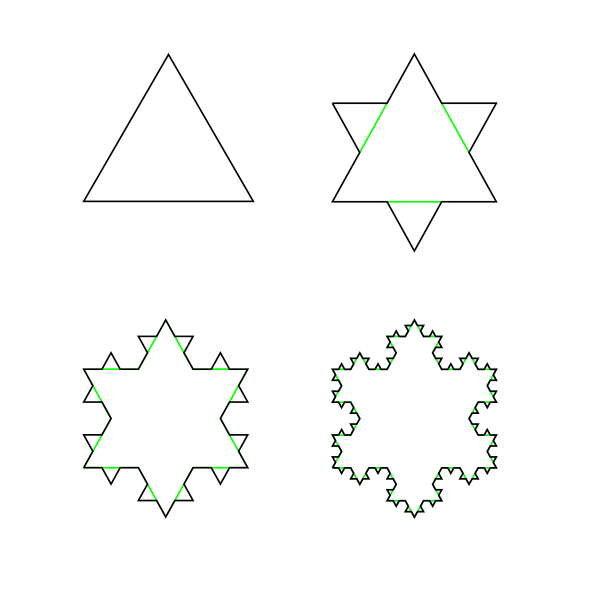
Start with an equilateral triangle, that’s a triangle with equal length sides. Then split every edge into three parts, and replace the middle section (shown in green above) with two sections equal in length to the piece removed. That’s your second level snowflake, now with twelve edges. Now repeat the process as far as you like, always replacing the middle section of an edge with two identical sections – the first four levels are shown above. The fractal shows self-similarity because if you zoom in on any particular section (known as a Koch curve), there would be no way of knowing how much detail the snowflake had been drawn to. The diagram below shows five iterations, but the snowflake it’s part of may go hundreds of iterations deep.

The Koch snowflake has some fascinating and borderline discomforting properties, as do most fractals. As can be seen from the diagram above, in every iteration a Koch curve becomes $\frac{4}{3}$ of the length of the previous curve, because every edge is split into three sections and replaced by four sections. Let’s have a look at the perimeters of the first four levels of a Koch snowflake, where the perimeter of the first level snowflake is, say, 27:
| Level | Perimeter |
|---|---|
| 1 | $27$ |
| 2 | $27 \times \frac{4}{3} = 36$ |
| 3 | $36 \times \frac{4}{3} = 48$ |
| 4 | $48 \times \frac{4}{3} = 64$ |
Note that the perimeter increases by 9, then 12, then 16. The perimeter not only increases in length, but increases by increments that get larger and larger. The perimeter simply gets longer and longer the more iterations you perform. We say that the shape’s perimeter ‘tends to infinity’. This snowflake’s an avalanche.
And this is all fine, except a glance at a series of Koch snowflakes does not seem to suggest a shape getting ‘infinitely bigger’…
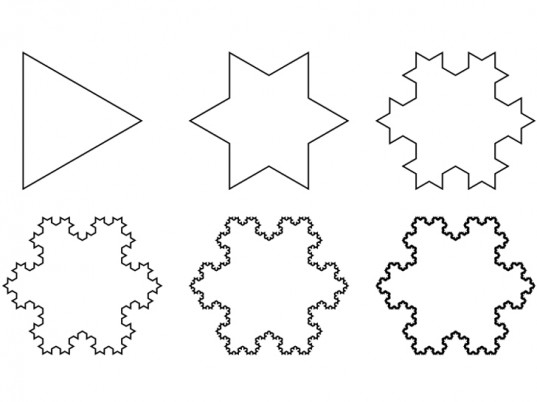
It seems that the area enclosed by the Koch snowflake does not tend to infinity. Here are the areas of the first four levels of the same snowflake as earlier:
| Level | Approx area |
|---|---|
| 1 | 36.1 |
| 2 | 46.8 |
| 3 | 52.0 |
| 4 | 54.3 |
Clearly, though these areas are increasing, the rate at which they are increasing seems to be slowing. Indeed, draw any level Koch snowflake and its area will remain well below twice the area of the original level 1 snowflake (actually the limit is eight fifths of the original area – the maths behind it is laid out nicely on Wolfram, for those interested.)
Let that sink in – the perimeter of the Koch snowflake tends to infinity, but the area it encloses does not. Does that hurt your head? As the number of sides tends to infinity, you end up with a Koch snowflake for which there would not be enough ink on earth to draw the outline, but a single biro could shade the inside.
There are many shapes in nature that approximate fractals, such as that of the bronchioles of human lungs, or Romanesco broccoli (which becomes even more delicious when you realise it is fractal in nature – quite literally.) Look at the picture below. Is it of several huge broccoli next to each other, or a zoom into one small piece of broccoli? At a glance it is hard to tell.

Of course this isn’t a perfect fractal – the self-similar shape does eventually come to an end when you zoom in far enough. But it’s the best example people tend to find for a real-life fractal. I have a theory that there is one example of naturally occurring infinite self-similarity though – fractal envy. To explain it, let me tell you a little story about Isaac…
Isaac is a musician, or rather fancies himself as one. He’s been playing a couple of acoustic covers at his local open mic night, occasionally even throwing in one of his own compositions. He loves doing it and it breaks up his working week, but he can’t deny that he’s a little jealous of Emmy, who frankly steals the show whenever she plays.
Emmy has a certain star quality that Isaac just doesn’t possess, holding the audience in the palm of her hand whenever she plays guitar. But Emmy isn’t happy – she knows her songs are good enough to break out of the local scene but she doesn’t know how to do it. She’s waiting on an email back from Sophie, who frankly she’s a little envious of.
Sophie goes under the stage name ‘Sophie Wonder’ and she’s making minor ripples on the national music scene after winning Glastonbury festival’s emerging talent competition. Since this happened she is able to tour nationally to hundreds of fans a night (this is where she met Emmy) and gets some national radio play. She probably isn’t going to return Emmy’s email though, because she’s trying to change management. Since hitting minor fame she’s realised that a million Youtube hits doesn’t actually make you any money, and touring at the level she currently is will leave her broke and homeless unless she steps it up a gear. She needs proper management like Leonhard has (honestly, she’s a little jealous of Leonhard…)
Leonhard is the singer and main songwriter in the band ‘Cantor Dust’, who have toured relentlessly over the last few years, since their debut album was named album of the year by 6 Music and the Guardian. They’ve gone from 50 capacity pub backrooms to arena shows in Europe and America, and they’re being touted as future festival headliners. But Leonhard is tired. He’s tired of playing songs he wrote five years ago while his management makes plans for three years’ time. He’s tired of living on the road, never being allowed to settle in one place for more than a few weeks. And he’s tired of making rock music in a world that no longer seems to want it. He never thought he’d say this, but he’s jealous of the producers and rappers making beats in their bedroom and playing the same festival stages he needs a whole band and crew for. If only he could be like Ada then he’d have it made.
Ada is truly at the top of the musical tree. One of the music world’s most in-demand producers, she can also summon eye-watering fees for DJ sets around the globe. She stays in the most lavish hotels and flies first class from recording session to festival to red carpet event. So why does she feel so empty? Perhaps because everything she does in her professional life presents a yardstick to measure herself against other people. Sometimes she can’t remember if she even likes the music she makes any more, but there’s so much pressure from so many people to make huge records that she’s forgotten how to reverse the tide. On lonely transatlantic flights she finds herself lost in thought, jealous of the folks who can still go down to the local open mic night without pressure and play a couple of acoustic covers.
(Images via Wikipedia and fractalfoundation.org. Isn’t it wonderful that there’s a fractal foundation?)
So, which bit of maths has tickled your fancy the most? Vote now!
Match 4: Group 4 - Colin Beveridge vs Kyle D Evans
- Kyle Evans with fractals
- (61%, 103 Votes)
- Colin Beveridge with the Sagrada Família
- (39%, 67 Votes)
Total Voters: 170
This poll is closed.
The poll closes at 9am BST on the 5th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.
Come back tomorrow for our fifth match of the group stages, featuring Grant Sanderson, and Alaric Stephen. Or check out the announcement post for your follow-along wall chart!
Can you not fix Kyle’s “four-thirds” representations? Or is 27 × 43 = 36 left as an exercise for the reader?
Oops, well spotted! I’ve TeXed it up now.
as a half-German, always thought Koch was pronounced as follows: https://www.youtube.com/watch?v=mJaw02iPbqo
the guy’s swedish though so who knows…..would be interesting to resolve whether or not I’ve been saying it wrong for decades!