Welcome to the 179th Carnival of Mathematics. The Carnival is a monthly post, hosted by a different maths blog each month, collecting interesting mathematical content from all over the internet. This time, we’re on home turf – here at the Aperiodical, with a post by regular guest author Paul Taylor.

179 is not a spectacularly fascinating number. But it is prime, so it has several properties that if not exactly interesting are at least named, thanks to mathematicians’ love for coming up with debatably notable subsets of primes and calling them things. Since you can subtract two from it; subtract one from and then halve it; or add one to then double it without affecting its primeness, it is in fact a safe Chen Sophie Germain prime.

The Carnival of Mathematics welcomes readers with any level of mathematical expertise; but should you ever need to gauge your general level of higher maths ability, or just fancy having a go at an interesting variety of maths questions, you could try this test from Math Vault.

After tackling the test you might need to de-stress, so why not have a go at some arts and crafts, like building Platonic solids from drinking straws and pipe cleaners. Or for even more low-effort relaxation, just watch this video of some takeaway pizzas demonstrating the concept of π:

If you prefer your maths Twitter content to have fewer amusing videos and more eight-tweet threads explaining Clifford algebras, try the one below from John Carlos Baez (click the timestamp to go to the full thread). Other submissions in the ‘explanations of somewhat meaty maths concepts’ this month include a summary of how to obtain the various equations of motion from Ari Rubinsztejn and an introduction to the Runge-Kutta methods for solving equations numerically, from John Cook.

Mark Dominus has shared some highlights from his blog: a reassuring look at a really smart person getting something completely wrong; the original rules for natural deduction proofs from 1934, which have stood the test of time remarkably well; and some thoughts about the ‘greatest common multiple’ and ‘lowest common divisor’.

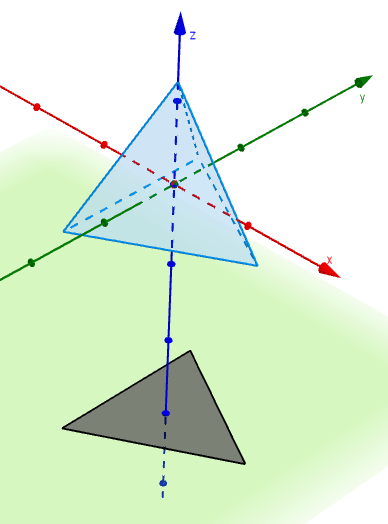
By now you’re probably thinking back to that drinking-straw tetrahedron you made, and wondering whether you could make an identically-sized solid tetrahedron and then cut a hole in it large enough to pass your original tetrahedron through. Well, Sam Hartburn has the answer.

Thanks for reading this month’s Carnival of Maths! Don’t forget, you can always submit interesting blog posts you’ve seen or written to future Carnivals, or offer to host one yourself – details of how to do both are on the Carnival of Mathematics page. The next Carnival will be hosted by Kevin Knudson.