Welcome to the tenth match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

Andrew Stacey – Keep Them Shutters Rollin’

Andrew Stacey writes about maths at loopspace.mathforge.org and tweets at @mathforge.

Mathematics is the playground of the mind,

and computers are the playground of Mathematics.

One of the selling points of Mathematics is that it is a place where we can let our imaginations roam free, and the ubiquitous “What use is it?” is given short shrift with a “I don’t know … yet. Wait and see.”. That our ideas don’t actually have a physical reality is of little import.

Nevertheless, it can be interesting at times to visualise these ideas. To see them and watch them play out. This can be tricky if they don’t correspond to an actual physical situation.

Enter the computer. Where we can let our free ideas run wild.

Most often, this goes under the guise of “simulation”, but this feels like a reductive word for something that can be as important as the Mathematics itself.

Let me illustrate with an example.

Rolling Shutters

The rolling shutter effect is possibly well-known, but if you’re one of today’s 10,000 let me give you a quick run-down. (For a more detailed introduction, take a look at Matt Parker’s video.)

It is based on the fact that some cameras take a picture not all in one go. Rather, the image is scanned, usually horizontally, and each part is “baked” as the scanning line goes past. Most of the time this goes unnoticed, but under certain circumstances it can produce quite weird effects because different parts of the image are laid down at very slightly different times.

It’s a very similar effect to that of some movie intros where the main character walks across the screen and is “frozen” in place at certain points to create a montage.

The classic, and the one we’ll devote our time to, is when an object is moving at sufficient speed that its motion is evident in the roll. If it is moving in the same direction as the roll then it will be elongated, if in the counter direction then foreshortened. Where this gets interesting is if it changes direction mid roll or rotates like a fan.

Another example of this phenomenon that I just want to mention in passing is where there is a sudden change in lighting mid-shot, as might be provided by a lightning strike.

Experimenting

Let’s go back to the basic rolling shutter and the classic image: a rotating fan. If doing this manually – by which I mean with an actual camera with a rolling shutter and a real fan – then it can take a bit of experimentation to get the fan to rotate at the right speed to see the effect (see Matt Parker’s video). The difficulty here is that the shutter is unknown as it will be buried inside the camera so all knowledge of what speed it travels at has to be inferred from the experiments. Fortunately we live in an age of digital cameras and can get near instant feedback, but nevertheless it can be a little tiresome.

Enter the computer.

With a computer we can simulate a rolling shutter. I’m using an iPad with an amazing programming app called Codea (disclaimer: I don’t get paid to say that Codea is awesome, I just say it because it is). This gives me a little more mobility in where I point the camera. The important part of the program is a thing called a shader. This determines how the camera image is written to an image and can exercise considerable control.

Using a program, we can adjust the shutter speed to the fan and so take our pictures in a more leisurely fashion. We can also experiment with different ratios of shutter speed to fan speed. In this picture, the fan does a half rotation in the same time as a single shutter pass.

(The slight glitch is because I’m cheating even more than necessary. Because I did a lot of experiments to generate all the pictures, I took a video of the fan and used it on loop. The glitch corresponds to where it starts again.)

On Beyond Zebra

Once we have a program, we have the ability to mess with it. In a standard rolling shutter, the image is baked at a linear speed from one side to the other. Let’s play the “What if?” game!

1. A fan moves in a circle, meaning that the ends of the blades don’t move across the screen at a constant linear velocity. What if the image were baked so that it matched the linear velocity of the ends of the fan blades?
   
2. What if we baked the image from left to right and top to bottom?
   
3. What if we baked the image from outside to inside?
   
4. What if we baked the image from outside to inside, but using a circular aperture?
   

To Infinity and Beyond!

One of the nice things about how shaders work is that the information they need is local rather than global. So instead of saying “At time $t$, these are the pixels to bake.”, we give each pixel a time and say “Bake yourself at this time.”.

Mathematically, therefore, to specify a generalised rolling shutter we need a baking function $b \colon [0,1]^{2} \to [0,1]$. Here, the domain $[0,1]^{2}$ parametrises our image and the codomain $[0,1]$ parametrises the time from when the shutter button was pressed (we make it bounded so that we can read off the image after a finite time – in practice, there are a finite number of pixels so this doesn’t actually limit us).

In other demesnes, this would be called a height map or a heat map.

With shaders, we can either specify this function as an expression or as another image, using the intensity of a point to determine the baking time.

Here’s a few random ones.

1. With the domain rescaled to $[-1,1]^{2}$, take
   $$
   b(x,y) = \frac{1}{4}\left ( \sin (2 \pi x) + \cos (2 \pi y) + 2\right )
   $$
   
2. Also with the domain rescaled to $[-1,1]^{2}$, take
   $$
   b(x,y) = \left |\left |x\right | – 0.5\right | + \left |\left |y\right | – 0.5\right |
   $$
   
3. Baking map given by taking the red channel in a random picture I have on my computer.
   
4. Baking map given by taking the red channel in a famous Mathematical picture.
   

Sam Hartburn & Lucy Rycroft-Smith – No-one is Going Anywhere

Lucy and Sam were writing lyrics together long before they met in person. They are now applying their considerable talents to remote collaboration for the Big Math-Off. Sam tweets at @SamHartburn and Lucy tweets at @honeypisquared.

We shall not cease from exploration
And the end of all our exploring
Will be to arrive where we started
And know the place for the first time.

T. S. Eliot, Four Quartets

Every journey begins with one step, be it physical or metaphysical.  Seemingly, everyone in the Western world also has a favourite social media platitude about self-discovery that improvises on this basic tune: you might move from one geographic place to another, but unless you yourself are moved, you will have gone nowhere at all. This sense of moving to mean a strong stirring emotionally as well as physically has only been around since the 1650s, but the intriguing idea of constant motion but never getting to one’s (real) destination is thousands of years old, and is mathematical as well as philosophical in nature.

Sitting on our sofas, confined to our homes, finding our excitement narrowed down to peeping out of our windows and a daily local walk if we’re lucky, we’re not going anywhere very fast right now. It might seem an appropriate time to pause and consider what it is to go on a journey, and how we know when we’ve reached our destination.

Moving – but never getting anywhere

Many years ago, a man named Zeno came up with a paradox. Several paradoxes, actually, but they had one thing in common – the idea of infinity. The one that is resonant here is the Dichotomy Paradox, and it goes something like this:

A goddess wants to travel to Athens. First she has to cover half the distance. When she has done this, she has to cover half the remaining distance. Then half the remaining distance from there, and from the next point, and so on. The remaining distance can always be divided in half, and she will always have to cover that half before arriving at Athens, so logic dictates that she will never arrive.

Philosophers spent a lot of time trying to ‘solve’ this paradox, but a satisfying conclusion was never reached. Observation of the physical world leads us to believe that people are able to travel from one place to another, so in one way the paradox can be seen as nonsense. On the other hand, there are no obvious holes in the logic. We like to think of whole generations of philosophers learning of the paradox and becoming paralysed with shock at the failure of their trusty logical methods, thus inadvertently proving the ‘no-one is going anywhere’ hypothesis true, if only individually.

Help!  How the heck does anyone actually travel anywhere?

No no, no no no no, no no no no, actually yes there is a limit

Cauchy to the rescue!  The French mathematician resolved the problem in some sense in the nineteenth century – not by walking to Athens, but by defining the concept of a limit. When the values in a sequence get closer and closer to some number, that number is said to be the limit of the sequence. For Zeno’s Dichotomy Paradox, the first term in the sequence is $\frac{1}{2}$, as this is half the distance to be covered. The next term is half the remaining distance, $\frac{1}{4}$, and the next is half the still-remaining distance, $\frac{1}{8}$, and so on. So the sum becomes

\[ \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\cdots =\sum\limits_{n=1}^{\infty }{{{\left( \frac{1}{2} \right)}^{n}}} \]

Cauchy showed that this series gets closer to 1 as more terms are added, but never reaches it, so the limit of the series is 1:

\[ \sum\limits_{n=1}^{\infty }{{{\left( \frac{1}{2} \right)}^{n}}=1} \]

This become apparent when you calculate and graph the first few terms of the series:

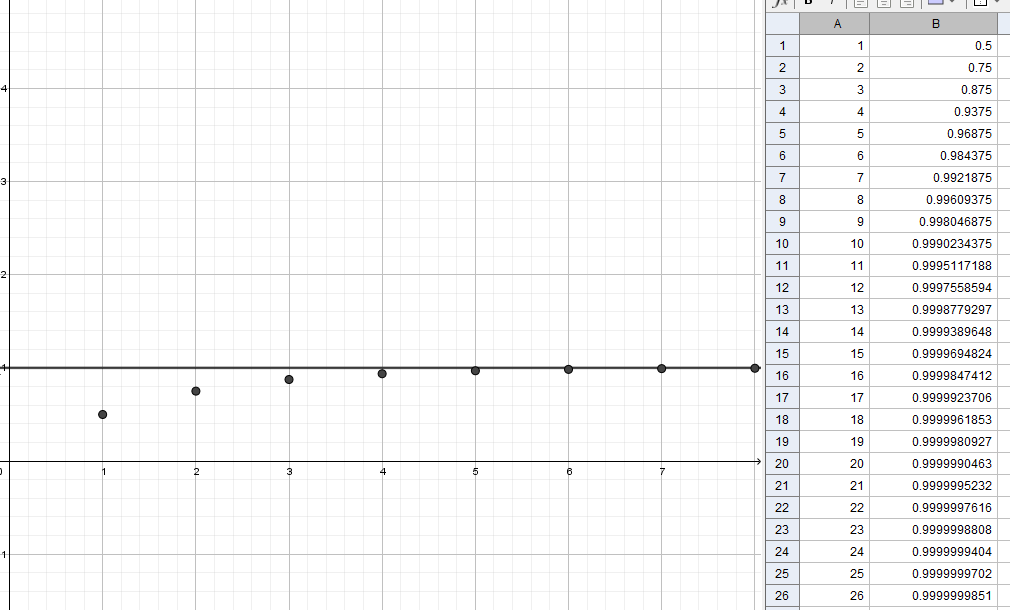
The points very quickly get so close to 1 that you can’t see the difference. But philosophically (and geographically), of course, whether we just get super close to our destination or actually reach it matters.

Aristotle wrote that ‘That which is in locomotion must arrive at the half-way stage before it arrives at the goal.’ Kylie Minogue wrote that ‘everybody’s doing a brand new dance now; c’mon baby, do the locomotion.’ Can we visualise this idea musically?

Music that moves you

The idea that inspired this article was this page in Evelyn Lamb’s Page A Day Maths calendar.

Source: Gareth E. Roberts, From Music to Mathematics: Exploring the Connections (ISBN: 978-1421419183)

It shows a series of notes, with each note being half the length of the one before it: minim, crochet, quaver, semi-quaver, and so on. This pattern, if continued to infinity and added together would be the same length as a semibreve (which is twice the length of the original minim).

Wait – what? How can an infinite number of notes be the same length as one semibreve?

 It’s mind-boggling!

Going through the motions

Might it help to visualise what’s going on in other ways? This sequence of circles starts with an empty circle, and half the remaining area is filled in each step.

As an animation, this evokes a sense of time slowing down, as if we are waiting for something that gets closer and closer but never arrives. The end of lockdown, perhaps?

There’s also the classic joke about mathematicians ordering drinks, which goes something like this:

An infinite number of mathematicians walk into a bar. The first one orders a pint of beer. The second orders half a pint. The third orders a quarter of a pint. At this point, the bartender stops them, pours two beers and says, ‘Come on, now.  Know your limits.’

Deadpan on arrival

Our favourite way of dealing with this paradox has to go to Diogenes the Cynic, who, according to Simplicius, said nothing, stood up and pointed to a destination across the room (presumably with an excellently sarcastic face on) and marched straight over to it. BOOM!  Mic drop, Zeno, you chump.

More serious refutations have often centred on the idea that instants in time and instantaneous magnitudes do not physically exist – that we are discretising that which is continuous, and so ‘breaking’ space and time. Take that, Zeno, you Planck.

If, like us, you feel that the idea of broken space-time is particularly resonant at the moment, or that you are currently in a hamster-wheel dynamic of perpetual motion but going nowhere fast, stay tuned!  Future Big Math-Off entries from the dynamic duo of Hartburn and Rycroft-Smith will promise to take you on a beautiful journey.  And maybe you’ll arrive back where you began, but somehow…moved.

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Friday the 1st, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.