Welcome to the fifth match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

James Munro – The Eggbox Puzzle

James is Admissions and Outreach Coordinator for Maths at the University of Oxford, and on a quest to find the biggest triangle @BiggestTriangle.

Can I offer you a nice puzzle about eggs in this trying time?

I’ve got three eggs and one long thin eggbox which has six spaces for eggs in a row.

There are 20 ways that the eggs could be put in the box, and I’d like to take photos of all the possibilities. I’m worried about breaking the eggs, so in between photos I will only move one egg, and I will move it exactly one space along in the eggbox. Here’s a gif of me (very carefully) demonstrating a safe move.

I’d also like to avoid unnecessary moves, so no photos should be repeated. The puzzle is to find a sequence of 20 photos that follows these rules, or to prove that it’s impossible.

If you haven’t seen this before, you should take a break now to try to solve it before I give away the answer. Get cracking!

My approach was to draw a graph of the possible egg configurations. The nodes of my graph are points in $Z^3$ with coordinates $(x,y,z)$ where $x$, $y$, and $z$ are integers representing the spaces that the eggs are in, with $1<x<y<z<6$. There are edges between two nodes that differ by exactly one in one coordinate only.

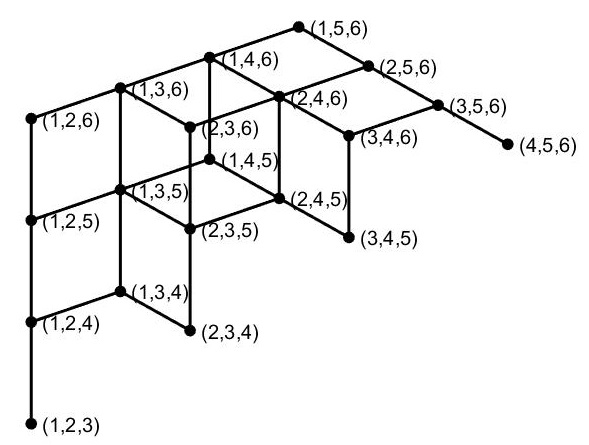
I’d like to find a Hamiltonian path on this graph. Unfortunately, there are no good algorithms for this in general, so I resorted to trial and error. To simplify the search, I looked for solutions that had the symmetry “reverse time and reflect the eggbox”. On the graph above, this is a reflection in the plane $x+y+z=10\frac{1}{2}$. With a bit of trial and error, I found a solution and carried it out in my kitchen.

Something rather nice is that swapping the eggs and the empty spaces gives me a different solution (and not just the reverse of the solution I’ve found). In general, inverting a solution for $n$ spaces and $r$ eggs would give a solution with $n$ spaces and $n-r$ eggs.

I’ve since eaten one of the eggs for lunch, leaving only two. It might seem easier with fewer eggs, but this version of the puzzle (six spaces in the eggbox, only two eggs) is impossible! I’ll leave the proof of that as an eggs-ercise for the reader.

Creative Crocheter – Crocheting Symmetries: A Matter of Scale

CreativeCrocheter is the pseudonym of a person who blogs about crochet and maths.

When considering what patterns might be found in a crocheted piece, a lot depends on how closely you look. A recent experience asking math students to identify the patterns present in an afghan and cushion that I had crocheted really brought this home. The afghan is made from 16 strips, no two of which are alike, using 4 solid colored yarns and one variegated yarn. Based on simple rules for which yarns to use in each strip and in which positions, the 16 strips represent all possible combinations.

The cushion is made from the same yarns and follows some of the same rules as used in the afghan strips.

What are those rules and what patterns result from them?

I titled the learning station at which the afghan and cushion were placed “Symmetries on the Euclidean Plane” and invited the students to contemplate the following:

1. Which solid-colored yarn was used more than the others? On what do you base this assessment?
2. List the three types of plane symmetries.
3. Examine the afghan: for each type of symmetry you identify, note it fully on a sticky note (one per note, please!), initial the note, and retain it for use during the talk.
4. Examine the cushion: for each type of symmetry you identify, note it fully on a sticky note (one per note, please!), initial the note, and retain it for use during the talk.
5. Look for other patterns in the afghan and cushion and note each on a separate sticky note in the same manner.

I also offered a bonus for fiber folk to consider: What rationale might explain the choice of which strips to put on the ends?

…Stop here if you’d like to take a look for yourself before seeing what I had in mind. Not that that turned out to be what the students saw…

So what was the method to my madness? For the afghan, I grouped the four solid colored yarns into two lights (sandstone and orange) and two darks (brown and dark green). For each strip, I used the variegated yarn, one dark yarn, and one light yarn.

Each strip was worked from the center out, with the four rows following this pattern: color A (down the center), color B, color C, color B. I chose to use the variegated yarn in only the A and C positions. This leaves two possible arrangements of the solid colors in each strip. Since there are 4 ways to combine the light and dark colors, this gives 16 possible combinations: 2 positions for the variegated yarn * 2 ways to position the other two yarns * 4 combinations of light and dark yarns. Under this arrangement, each solid color is used the same number of times in each of the possible positions it can take—so yes, that’s a trick question in item #1. The same amount of each solid color yarn is used in the afghan strips. Well, theoretically anyway. In actuality I had more green and less orange left over after finishing the afghan and before starting the cushion. Some possible reasons are that some of the solids had more or less yarn per skein than the label claimed, some yarns worked up differently (some did feel thicker than others, so my gauge might have varied), or I did something different on some strips (such as leaving longer yarn tails to weave in).

Given the construction rules for the strips, there were numerous possible rules for how to arrange the strips. A friend with superb color sense helped me lay them out, with much tweaking and rearranging until we found an order that was both aesthetically appealing and had an internal logic that engaged my mind. The most obvious of those internal patterns is seen by considering only where the light and dark yarns are positioned, without regard to which were used for each. When viewed in this way, the two halves of the afghan mirror each other, across a line between the center two predominantly orange strips. This reflection symmetry is actually easier to see in the photo than in person, because the photo blurs the distinction between the brown of the top strips and the dark green of the bottom strips.

Another very obvious reflection symmetry is that the end of each strip mirrors the other end. In addition, there is a mirror symmetry from side to side within each strip. That is, before the strips were connected to each other, folding them in half in either way makes the colors match up—with one caveat I’ll get into shortly. Because of the mirror symmetries in both directions, each strip also has a rotation symmetry, with a rotation angle of 180°. This is of course a direct result of their construction method because each strip was worked in the round around the initial row.

The third type of symmetry in the Euclidean plane is a slide or translation symmetry. This is seen within each strip, where a group of stitches can be thought of as repeating itself down the length of the strip. In addition, when color is ignored completely, each strip is a translation of its neighbor.

So what about the cushion? It was crocheted as a tube, with the tips at each end pulled together to form the center of each side. While the color order and number of rows of each color were not as thoroughly planned out as the afghan, the cushion does retain the symmetries that can be seen by grouping the light and dark yarns. The two sides of the cushion have the same pattern of lights, darks, and variegated yarns, with only a change in which light or dark yarn was used. For example, the center of one side is dark green, while the center of the other side has the same number of rows in brown. The four rows of variegated yarn around the edge is where the color mirroring switches. Because of the zigzag pattern and the tube construction, the symmetry actually combines a reflection with a glide. In addition, each side of the pillow shows a 10-fold rotation symmetry.
In thinking through what I expected to hear when I asked what patterns the participants had found, I envisioned a matrix of answers with columns based on the level to which the pattern applied and rows representing the type of pattern observed.

Across top:

1. Color pattern
2. Stitch pattern
3. Row pattern
4. Strip pattern
5. Relationship between afghan and cushion
6. Other

Down side:

1. Sequence
2. Reflection
3. Translation
4. Combinatorics (each strip has a unique combination of colors and placement of those colors)
5. Equivalence classes
6. Other

While the math students had a fairly easy time identifying the symmetry patterns, no doubt primed by being asked to name the types, I was surprised that they found so few of the other patterns I see. As it turned out, a rather high percentage appeared to have some form of colorblindness, so the color-based patterns were lost on them. I wonder whether non-mathy fiber folk would have had a more diverse set of responses.

Ah, you want to know why the strips with the dark colors on the outside rows were chosen to go on the ends? Because the ends are always what get dirty first, and the dark colors are less likely to show it.

No, I haven’t forgotten my caveat about the strips’ symmetry properties. Let’s take a closer look at the ends of one strip of the afghan. Notice how they are and are not mirror images of each other.

From an arms-length viewpoint, the ends look very symmetric. But on closer inspection, one may notice that the stitches are not themselves symmetric. So the two ends are therefore not, strictly speaking, mirror images of each other. Nor are the sides across the center of the strip.
Does any of this matter when considering how comfortable and colorful these items are? No, not really, though certain levels of pattern—particularly regularity and repetition—add visual interest and may even help define what we find aesthetically pleasing. On the other hand, the ability to step back and see patterns that were invisible at close range is certainly a skill that comes in handy in many areas of one’s life. What patterns caught your eye today?

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Tuesday the 21st, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lock-Down Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.