Welcome to the sixth match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.
You can still submit pitches, and anyone can enter: instructions are in the announcement post.
Here are today’s two pitches.
Zoe Griffiths – What’s wrong with Geistes Blitz (Ghost Blitz)?
Zoe Griffiths is a maths communicator for Think Maths. You can find her on Twitter at @zoelgriffiths.
Here is a zip file containing the cards and instructions for play for ‘Shape Match’:
Note, my observations are based on one edition of Geistes Blitz only.
Emma Bell – A beautiful cuboid puzzle
Emma Bell is Maths Enhancement Manager at Grimsby Institute. On Twitter she is @El_Timbre.
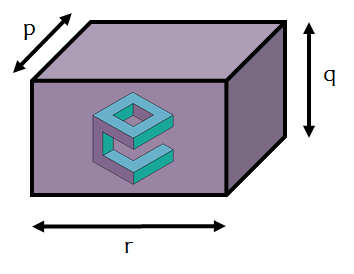
Calculate the volume of the cuboid, given that:
\begin{align} pq &= 10 \\
qr &= 18 \\
&\text{and} \\
pr &= 20 \end{align}
I love this “puzzle” because of the journey it takes you on as you solve it…
Have a play with it, and come back to hear my thoughts!
The first path I took was to see if I could use the given products to find the values of each of the separate dimensions.
\begin{array}{ccc}
pq=10 & qr=18 & pr=20 \\[0.5em]
\color{red}{q=\frac{10}{p}} & \color{blue}{r=\frac{18}{q}} & \color{blue}{r=\frac{20}{p}} \\[0.5em]
\color{green}{p=\frac{10}{q}} & \color{red}{q=\frac{18}{r}} & \color{green}{p=\frac{20}{r}} \end{array}
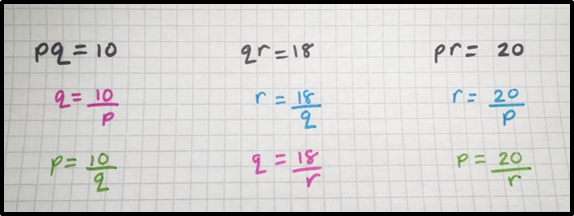
This looked promising! I had pairs of equations which I could group together, and perhaps the dimensions would fall out nicely?
\begin{align}
\color{green}{\frac{10}{q}} &= \color{green}{\frac{20}{r}} \\[1em]
\color{red}{\frac{10}{p}} &= \color{red}{\frac{18}{r}} \\[1em]
\color{blue}{\frac{18}{q}} &= \color{blue}{\frac{20}{p}}
\end{align}
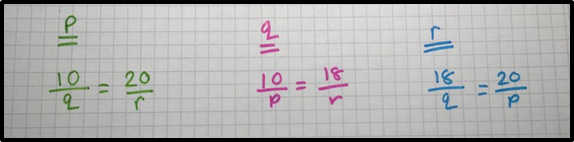
With some substitution and manipulation, I got there…
\[ \color{green}{
\begin{align}
\frac{10}{p} &= \frac{18}{r} \\
\frac{10}{p} &= \frac{18}{\left(\frac{20}{p}\right)} \\
\left( \frac{20}{p} \right) \left(\frac{10}{p} \right) &= 18 \\
\frac{200}{p^2} &= 18 \\
200 = 18p^2 \\
p^2 = \frac{100}{9} \\
p = \frac{10}{3}
\end{align} \\
\text{(+ve only!)}
} \]
\[ \color{red}{
\begin{align}
\frac{10}{q} &= \frac{20}{r} \\
\frac{10}{q} &= \frac{20}{\left(\frac{18}{q}\right)} \\
\left( \frac{18}{q} \right) \left( \frac{10}{q} \right) &= 20 \\
\frac{180}{q^2} &= 20 \\
180 &= 20q^2 \\
q^2 = 9 \\
q &= 3
\end{align} \\
\text{(+ve only!)}
} \]
\[ \color{blue}{
\begin{align}
\frac{10}{p} &= \frac{18}{r} \\
\frac{10}{\left(\frac{20}{r}\right)} &= \frac{18}{r} \\
10 &= \left(\frac{18}{r}\right)\left(\frac{20}{r}\right) \\
10 &= \frac{360}{r^2} \\
10r^2 &= 360 \\
r^3 &= 36 \\
r &= 6
\end{align} \\
\text{(+ve only!)}
} \]

\begin{align}
\text{Volume} &= p q r \\
&= \color{green}{\left(\frac{10}{3}\right)} \times \color{red}{3} \times \color{blue}{6} \\
&= 60 \text{ cubic units}
\end{align}
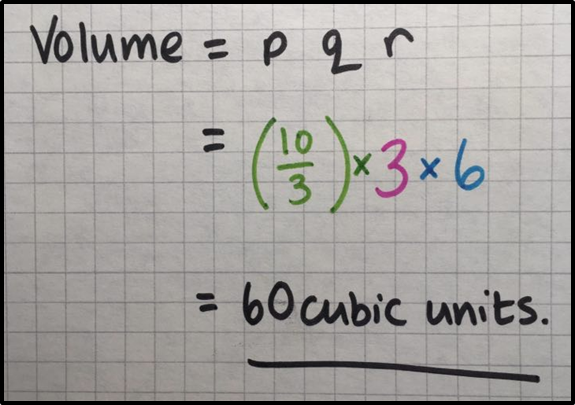
However, I wasn’t mathematically satisfied… yes, I’d reached a solution, but it didn’t seem elegant enough. It was too mechanical, and dare I say it, BORING…
I started again (and I’ll admit, it was handy to know where I was going!)
\begin{align}
(pq)(qr)(pr) &= 10 \times 18 \times 20 \\
p^2q^2r^2 &= 3600 \\
(pqr)^2 &= 60^2 \\
pqr &= 60
\end{align}
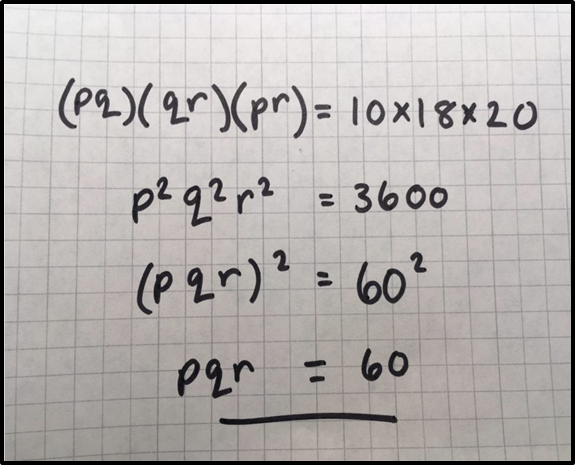
Now THAT’S beautiful!
So, which bit of maths made you say “Aha!” the loudest? Vote:
Match 6: Zoe Griffiths vs Emma Bell
- Emma with cuboid volumes
- (63%, 37 Votes)
- Zoe with Geistes Blitz
- (37%, 22 Votes)
Total Voters: 59
This poll is closed.
The poll closes at 9am BST on Thursday the 23rd, when the next match starts.
If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.