Welcome to the third match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

James Arthur – Cleaving Cats

James is a confused physicist disguised as a pure mathematician who calls the heart of Cornwall his home. By day he is a web developer and studying towards his degree at Exeter Penryn. By night, he is a differential geometer and an analytical number theorist. He blogs at AlephJamesA.co.uk.

We all like to talk about randomness and know how hard it is to recreate and gauge when things are actually random. I think that randomness is fascinating and as a geometer, the mixture of the two creates a favourite bit of maths and an enjoyable coding task.

1 Tori and Transfomations

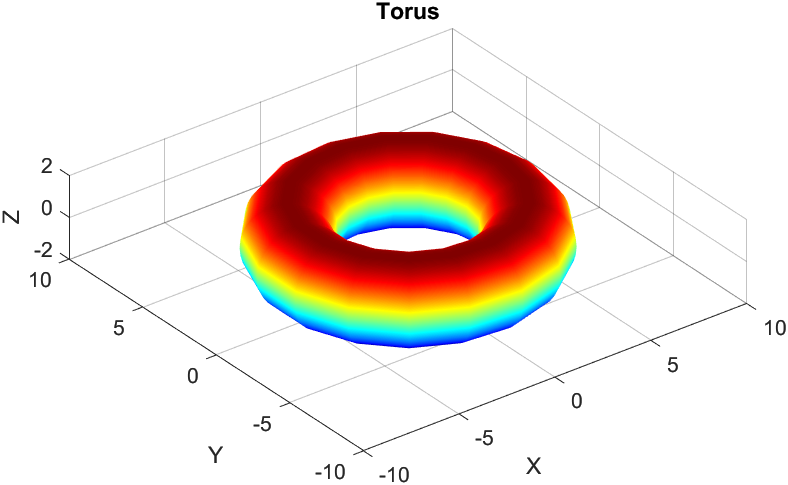
A torus is also known as a donut; it is a continuous surface that is the same as the edible snack. The surface can also be covered using rectangular strips of a certain length and width, but also, less intuitively be covered using triangles, with caveats. With the triangles, these can be made by skewing squares and rectangles, this can be done using linear transformations and linear systems of equations.

In relation to the matrices, we can define a shear in parallel to the x axis: $\begin{pmatrix}1 & a \\0 & 1\end{pmatrix}$ and in the y axis: $\begin{pmatrix} 1 & 0 \\ a & 1 \end{pmatrix}$

We can define a linear tranformation using a matrix and a vector, $v\textbf{A} = v’$ where $v = (x\quad y)^{T}$. So we could take a transformation parallel to the x axis and parallel to the y axis one after another. This would then produce rectangles which would nicely cover the torus.

\[ \begin{pmatrix}1 & a \\0 & 1\end{pmatrix}\begin{pmatrix}1 & 0 \\a & 1\end{pmatrix} =\begin{pmatrix}1 + a^2 & a \\a & 1\end{pmatrix}\]

If we just take the generic and simplest non-trivial case, of $n = 1$, we end up at a particular matrix. $\begin{pmatrix} 2 & 1 \\ 1 & 1 \end{pmatrix}$, this matrix is equivalent to the mapping: $\Gamma{(x, y)}\to(2x+y,\,x+y)$. Remember the caveat I mentioned earlier, this caveat is the fact you could get overlapping triangles wrapping around the torus parallel to the major radii. To stop this, you need to place a thing called a modulo N operator, this will wrap any number greater than N to the amount it is greater than N, i.e. $35\mod{6} = 5$. This makes the equations now: $\Gamma{(x, y)}\to(2x+y,\,x+y)\mod N$, but N is a number and one we must choose carefully.

2 Kittens of Chaos

At this point, we must go into greater detail about what we are deriving here. This is a system that you would expect to output chaos given what it does to an image. Let me show you a frame from a couple of iterations in. Figure 2 shows almost white noise that you would expect to see on an untuned analogue television, this came from a perfectly normal image of a cat. To deal with pixels individually, we will let N=1.

We know many cats are little fluffy gremlins, but this takes it to the extreme, this is Chaos. For something to be chaotic, it must tick the following three conditions:

• Sensitive to initial conditions; in this mapping, the initial conditions are the images you input
• It is to be topologically transitive; the outputs of the mapping gets flung out so much that there isn’t any overlapping of the outputs
• The mapping has dense periodic orbits; every point is either arbitrary close to a periodic point or is a periodic point.

If we input two different images, then the output would be different colours and would produce drastically different outputs. Even if we just edited all the white in Figure 2 to be yellow, it would be drastically different.

Take a small area of pixels in a border where the image is being split into triangles. The set is to be divided in half, and they are to be placed away from each other. Then they may be cut again and again and again, producing an almost dissolving effect. So the original set is mixed into the image. This is why topological transitivity is called a mixing effect. As seen in Figure 3, the triangles/quadrilaterals are picked between the subset and then they are split, and so the set is mixed into the set.

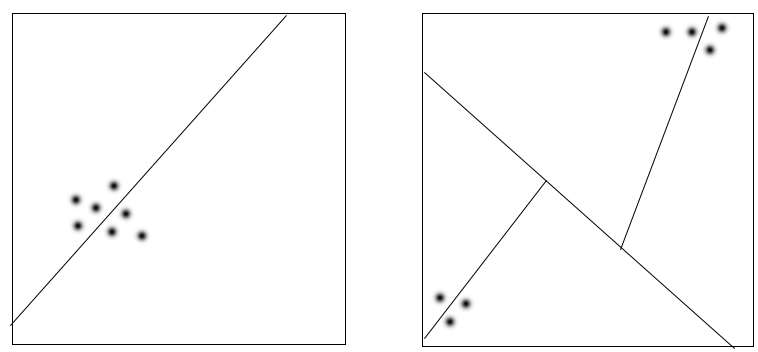
Figure 3: The Mixing Effect

To show that there are dense periodic points, it suffices to show that all points are periodic, to do this, we shall look at element cat_000 and cat_120:

(a) cat_000

(b) cat_120

Figure 4: Showing periodic points

Just a minute… that’s the same image… this chaotic sequence is periodic. It does all these weird and wonderful shears on the torus and eventually it just turns back into the original state of the torus!

This now proves that the mapping is a chaotic mapping, which is so aptly named the Arnold Cat Map.

3 Flows of Milk

In dynamical systems like this, to see geometric flow we study the eigenvalues of the associated matrix of the system:

\begin{align*}|A-\lambda I| &= \left|\begin{matrix} 2 – \lambda & 1 \\ 1 & 1 – \lambda \end{matrix}\right|\\&= (2 – \lambda)(1 – \lambda)- 1\\&= \lambda^2 – 3\lambda + 2 – 1\\&= \lambda^2 – 3\lambda + 1\\\implies\lambda &= \frac{3\pm\sqrt{9 – 4(1)(1)}}{2} = \frac{3\pm\sqrt{5}}{2}\\\therefore \lambda_1,\lambda_2 > 0 \text{ and } \lambda_1\neq\lambda_2\\\end{align*}

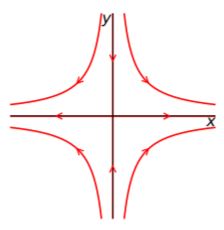
In systems of the form of differential equations, we could take information just from this. Still, we are working with recurrence relations, so we need to consider the Liapunov exponents. These exponents are just the eigenvalues with the numerator natural logarithmed: $\Lambda_{1, 2} = \frac{\ln{(3\pm\sqrt{5})}}{2}$. We are allowed to now use the same rules as eigenvalues and differential equations. So we know it must be a saddle point, which is of the form of Figure 5.

Given the output of the mapping, we know that the point at (0, 0) must be static and then the curve in the quadrants must be cyclic. Doing some sketching and some exploration of eigenvectors, you can approach the diagram in Figure 6.

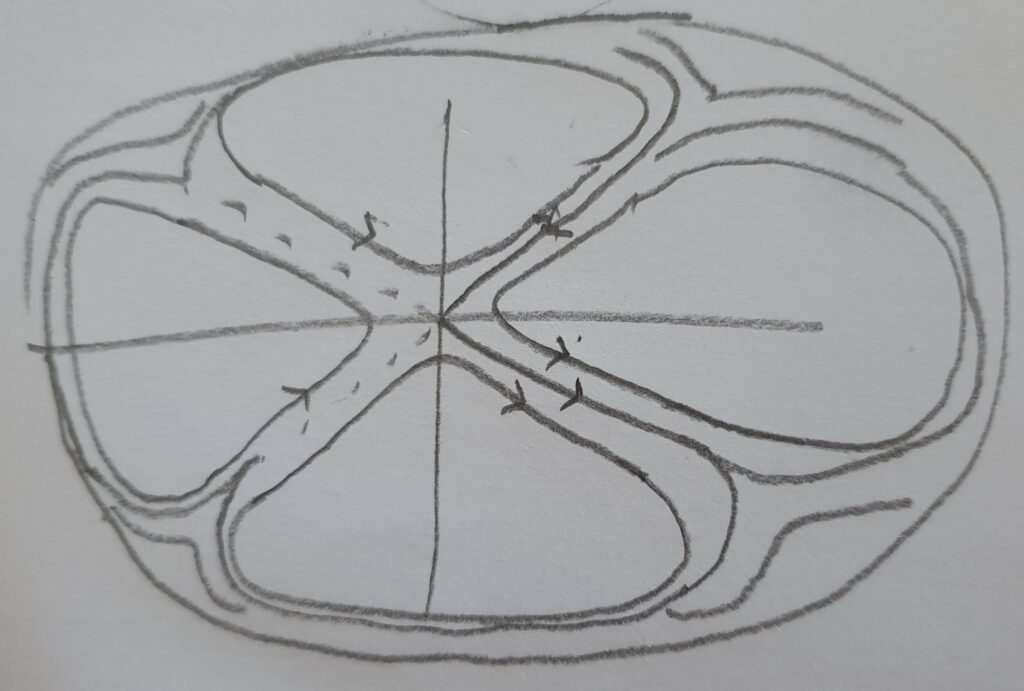
Figure 6: A Guess of the flows given the one equilibria

The Arnold Cat Map is an algorithm that jumbles up an image to near Chaos and ends up with the picture back in the original position. This is something you’d never expect from it at first glance. This is something of great interest and is the main reason I love Mathematics, it’s all about delicately pulling away the other less colourful petals to get to the beautiful rose inside.

I created some python to create the gif:

from PIL import Image
import numpy as np
import glob

# load image
im = np.array(Image.open("input.jpg"))
N = im.shape[0]

# create x and y components of Arnold's cat mapping
x,y = np.meshgrid(range(N+1),range(N+1))
xmap = (2*x+y) % N
ymap = (x+y) % N

for i in range(N+1):
 result = Image.fromarray(im)
 result.save("./images/cat_%03d.png" % i)
 im = im[xmap,ymap]
 print(i)
 
fp_in = "./images/cat_*.png"
fp_out = "./output.gif"

# https://pillow.readthedocs.io/en/stable/handbook/image-file-formats.html#gif
img, *imgs = [Image.open(f) for f in sorted(glob.glob(fp_in))]
img.save(fp=fp_out, format='GIF', append_images=imgs, save_all=True, duration=120, loop=1)

Katie Severn – Infinity

Katie Severn is an assistant professor in statistics at the University of Nottingham having recently finished her PhD in statistical analysis of samples of networks. She is a keen advocate of raising awareness of mental health issues in academia and celebrating the successes of minorities in STEM. Outside of coding and wrestling with data she has been spending her time during this pandemic painting and caring for an army of house-plants, not to mention a lot of (bad) singing and dancing. She’s @K_Severn on Twitter.

I’ve always been amazed by the concept of infinity. From a child saying I love ice cream an infinite amount (which I still stand by) to an adult statistician where infinity crops up in many proofs and theoretical results (1000 is close enough to infinity for my sample size right… right?!). Infinity is the concept of endlessness and is denoted the symbol $\infty$.

Using the concept infinity can lead to very counter-intuitive results. One that still baffles me comes from recurring decimals. A recurring decimal is one where digits after the decimal recur for infinity and is represented by a dot over the recurring digits. For example $0.\dot{9}$ represents:

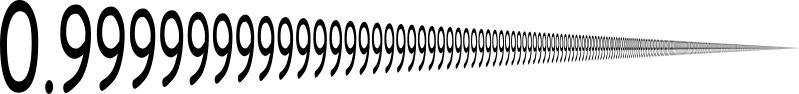
Now why is this interesting?! Well because of the concept of infinity in recurring decimals it is in fact true that

\[ 0.\dot{9} = 1. \]

And yes that it is an equal sign, they are not approximately equal or very close they are exactly EQUAL. And I can prove it! First set

\[ {\color\red{x}}=0.\dot{9}, \]

meaning

\[ 10{\color\red{x}}=9.\dot{9}. \]

This means

\begin{align}10{\color\red{x}}-{\color\red{x}}&=9\\9{\color\red{x}}&=9\\{\color\red{x}}&=1 \end{align}

so

\begin{align}0.\dot{9}&={\color\red{x}}=1\\0.\dot{9}&=1\end{align}

Another counter-intuitive result or in this case a paradox involving infinity is known as Hilbert’s paradox of the Grand Hotel:

I’ve turned up at the Grand hotel which has infinitely many rooms. Of course this is a hotspot resort for all mathematicians and unfortunately when I get there there are already infinity many guests, but instead of turning me away the receptionist says that’s fine we can make room for you.

But how is this possible when their are infinitely many rooms and infinitely many guests already, surely every room is taken? Well the answer is quite simple: get every guest to move to the room one more than the one they are in, I can then take room number 1 (which my beautiful pictures show). And as infinity is endless there will always be a room one more than the one you are in.

(You may wonder why they look so happy to be moving rooms and inconvenienced, well they are mathematicians at the infinite hotel – that’s bucket list stuff!)

Now in this previous paradox there is one key bit of information that makes it possible for me to get a room, and that is we are referring to countable infinity. Now this doesn’t mean we can count the infinity, we already know that infinity is endless, but it refers to the fact that there are actually different sizes of infinity! What that means is some infinities can be bigger than others.

A general idea of two different infinities is the set of natural numbers (positive whole numbers) and the set of real numbers (essentially all numbers, so include all decimals). The set of natural numbers I can write out as

1, 2, 3, 4, …, 101, 102, …, 1001, 1002, …

of course I can never write them all as there are infinity many but I can write them in an order that means I will never miss one out. However for real numbers I can’t do this, if I start

0, 0.1,

oops I’ve missed 0.01, no worries

0, 0.01, 0.1, 0.2,

what about 0.011

0, 0.01, 0.011, 0.1, 0.2

but what about 0.0101 and 0.01001 not to mention 0.001, 0.02 0.0112,… and so on.

Hopefully it’s clear that there is no way to write all the real numbers in a way that will mean everyone gets included, this is because between any two real numbers there is always another real number (this is not true for natural numbers, e.g. between 2 and 3 there is no other natural number). And it is this idea that means that the size of the set of real numbers can be thought of as a larger infinity then the set of natural numbers.

There’s many more tricks and paradoxes that involve infinity not to mention the vast amount of mathematical results that hinge of the concept of infinity (calculus I’m looking at you). I hope you’ve enjoyed reading about infinity even a fraction of the amount I enjoy it (and a fraction of infinity is still infinity so…).

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Friday the 17th, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.