Welcome to the 11th match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

Pat Ashforth & Steve Plummer – Maths or Art?

Pat Ashforth and Steve Plummer explore maths through knitting and crochet at woollythoughts.com.

In a previous match I talked about how perception might affect mathematical thinking. Here we are again with another example.

Are these the same?

Look at them with the eye of an artist and you will almost certainly say ‘No’. As a mathematician you might say ‘Yes’, or, at least ‘Maybe’.

You will definitely recognise this – or will you?

Most will instantly say ‘curves of pursuit’ – but is that right?

Technically, a pursuit curve is the path followed by the chaser in pursuit of the chased. This might be an animal pursuing its prey, one ship trying to catch another, or any other kind of chase. It is a single path. We usually see curves of pursuit where there are several chasers with each one pursuing the one in front and making pretty patterns. They don’t have to be in squares. Three equally-spaced chasers would make a triangle; six would make a hexagon. There can be any number of chasers. These are called cyclic or polygonal pursuits.

Right now we are only concerned with four chasers starting at the corners of a square field – but the squares you see above are not accurate cyclic curves. We have used artistic licence in our design. What you see are squares always rotated through the same angle. This is not what happens in a genuine curve of pursuit.

Assuming that all chasers are moving continuously at the same speed they will always cover the same distance in the same amount of time. The distance they move forwards will always be the same. This is not what happens in our design. The difference is not obvious on the first few squares but as you move further in you can see that the short side of the triangles remains the same throughout the ‘real curve’ but it is the angle that stays the same in the ‘artistic curve’.

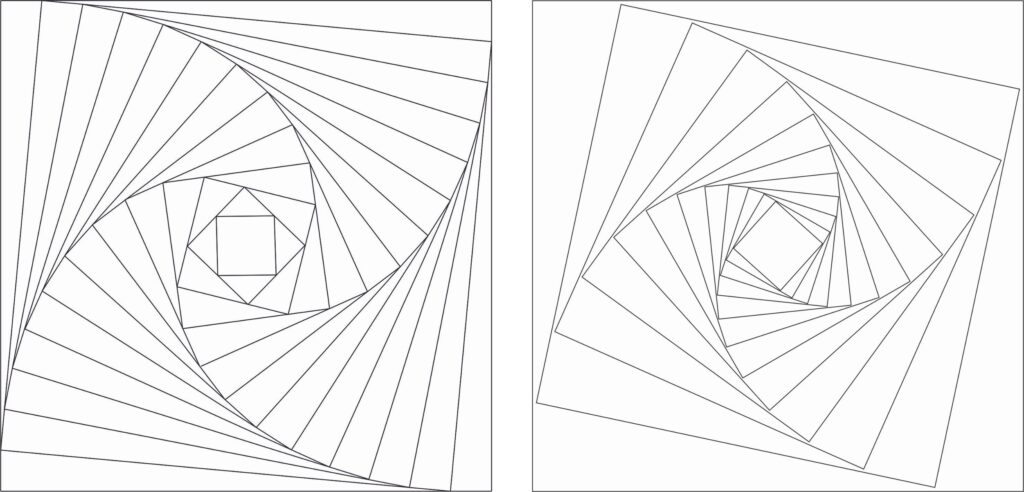
The ‘real curve’ would be extremely difficult to replicate in knitting, as a separate set of instructions would be needed for each set of triangles. The knitted version uses the same shaping technique throughout, which results in triangles with equal angles, instead of a matching side. Our chasers are changing their speed, but are always chasing one another. You have probably noticed that the squares in our version don’t quite touch the edges of the previous square. We know that lines in a drawing, theoretically, have no thickness. Woolly things have quite thick joins.

The knitting starts with the centre square and each new square is four triangles added to the sides of the previous square. Having established that the rest should be straightforward. Not so.

The story of the knitting pattern goes back a long way. Briefly, it was first published in 1997 and hundreds of people made blankets. After a few years we started to get complaints from people who thought they had received the wrong pattern. They wanted the one with curves, not squares. We spent so much time explaining that what they saw depended on the colouring they used, we had to find a solution. Colours often cause problems because people feel the need to use exactly what was used in the original. The solution had to be in shades of grey. We made nine different versions so everyone could find what they wanted.

This is our original blanket which was made with rather uninspiring colours that we just happened to have at the time. We never expected this to still be our most popular design, more than twenty years later. Is it due to the maths or the art?

James Arthur – Functional equations

James is a confused physicist disguised as a pure mathematician who calls the heart of Cornwall his home. By day he is a web developer and studying towards his degree at Exeter Penryn. By night, he is a differential geometer and an analytical number theorist. He blogs at AlephJamesA.co.uk.

This story starts where all other good stories start: at an International Mathematics Competition. It shall be a story of intrigue, betrayal and in the end success.

In the Summer of 2019 at Celtic Manor, a few miles from the Welsh Border. I was sitting in a conference room wearing my purple stellated icosahedron IMO t-shirt, sorting out bags to give to team leaders and other helpers at IMO. I was always a fan of the UKMT Challenges, and I had done the BMO2 that year and missed out on the Trinity Camp, but I was happy to have got so far. After all, I was at IMO anyway!

I spent a lot of time in the room chatting and sorting stuff out, I also spent a lot of time running about Celtic Manor doing several bits and bobs. My main job was helping out in the Jury Meetings. I was a microphone runner, so I spent a lot of time getting to know the delegates and everybody else there.

Shhh… look over here

Now here we see a lesser spotted functional equation, it isn’t seen very often out of IMO in the UK. It is neglected by the education system and so is innately shy.

\[ f(2a) + 2f(b) = f(f(a+b)) \]

It appeared on Day I of the 2019 Competition at Bath University. It was of much debate if I remember correctly, on whether it was too easy for the IMO.

How I came across it

While in a jury session, this problem took my interest. Functional equations had come into my find briefly in specific topics, especially when talking about Fibonacci Sequence and The Golden Ratio, but I had never studied them in great depth. I had just studied recurrence relations in excellent depth the term before.

I was sitting in the conference room working on a few problems that I was given by several delegates from other countries, they all took great interest in me, surprisingly! I was then handed a copy of this question, told to solve it and sworn to secrecy until later we found out it was on the paper. I had a problem, I have never solved anything like this before. Here is the exact problem:

Let $\mathbb{Z}$ be the set of integers. Determine all functions $f : \mathbb{Z}\to\mathbb{Z}$ such that, for all integers $a$ and $b$, $f(2a) + 2f(b) = f(f(a+b))$

… as in the paper, the version I was given was slightly different, but I believe that is still under embargo, so we shall go with this version.

While we are looking at this problem, we see that if $f(x) = 0$, then it would be a solution. We shall keep this in mind for later, and in particular, it’d be good to remember that if all the terms are in terms of $f$ then $f = 0$ is a solution.

The Road to Enlightenment

To solve this problem I was chucked through a crash course to solve these types of problems; I shall do a quick crash course for our purposes:

Types of Functions

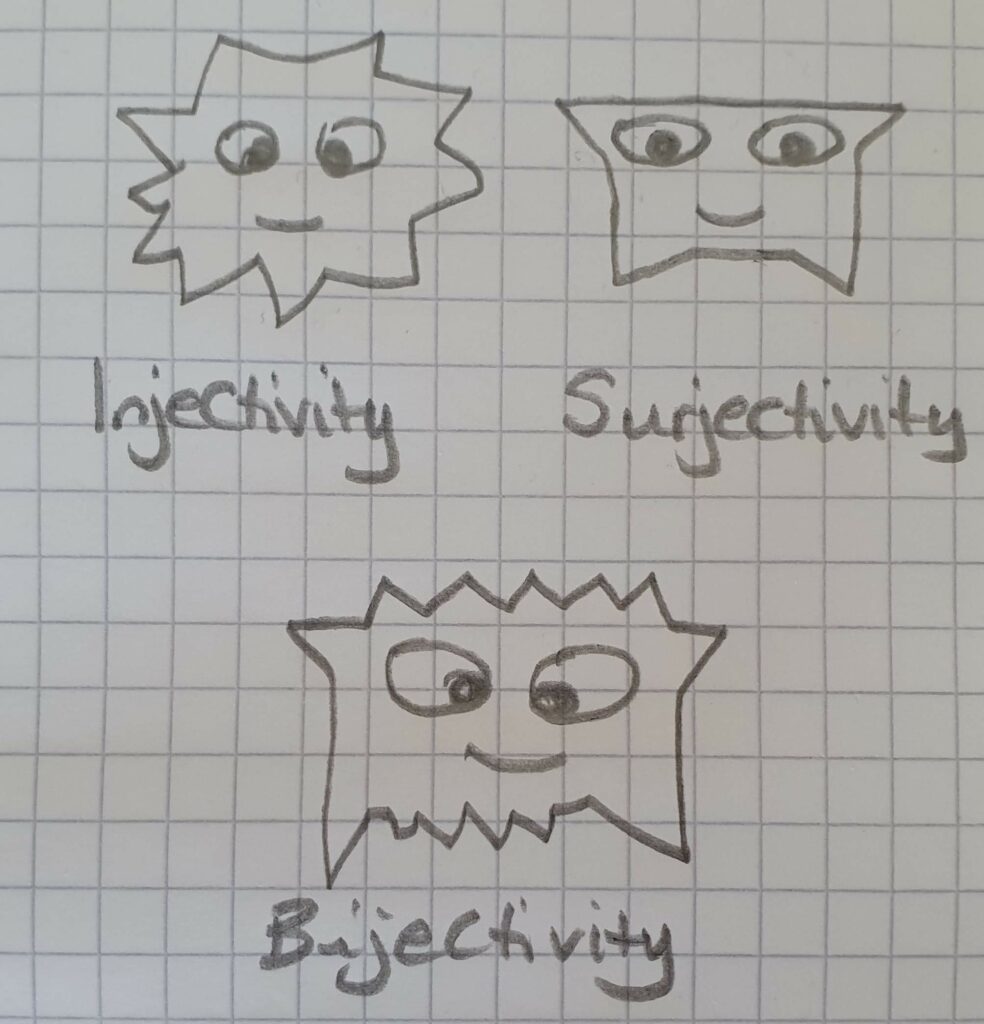
Three types of functions interest us: Injective, Surjective and Bijective. These really confused me, but I have got to grips with them now. They will be your little fluffy friends for Functional Equations. Friends that also are liable to bite the head off the problem, and so solve or it for you.

Def: Injective – Take a function from a set $A$ to a set $B$, $f: A\to B$, then if the values for $f(x)$ and $f(y)$ are equal, then $x = y$, i.e. $f(x) = f(y) \iff x = y$.

Def: Surjective – Take a function from a set $A$ to a set $B$, $f: A\to B$, then there is some elements of $A$ that satisfy $f(x) = b$.

Def: Bijective – Take a function from a set $A$ to a set $B$, $f: A\to B$, then it is sufficiently surjective and injective.

Learning By Example

The rest is a lot of plugging in and testing the outcome of substitutions. So let us take an example from IMO 2015, hosted at Chiang Mai, Thailand.

Let $\mathbb R$ be the set of real numbers. Determine all functions $f:\mathbb R\to\mathbb R$ that satisfy the equation $f(x+f(x+y))+f(xy)=x+f(x+y)+yf(x)$ for all real numbers $x$ and $y$.

Firstly let us look at this equation. We have a hanging $x$, we shall take this as a sign and let $x = 0$, letting $x$ and $y$ equal $0$ is usually a good idea to get an idea of what is going on.

\[ f(f(y)) + f(0) = f(y) + yf(0) \]

Now, we shall let $y = 0$ and simplify:

\[ f(f(0)) = 0 \]

Amazing, we have one piece of information, if we put $f(0)$ back into our function you get 0. So let us place $(0, f(0))$ back in using this information to try and get $f(0)$:

\[ f^3(0) + f(0) = f^2(0) + (f(0))^2 \]

Note that $f^{2n+1}(0) = f(0)$ and $f^{2n}(0) = 0$, so:

\[ \begin{align*}(f(0))^2 – 2f(0) &= 0\\f(0)(f(0) – 2) &= 0\\\implies& f(0) = 0 \text{ or } f(0) = 2\\\end{align*} \]

Now from this we shall let $f(0) = 2$ and come back to the other case later. Let us go back to the $x = 0$ substitution and let $y=x$:

\[ f^2(x) = f(x) + 2(x – 1) \]

We note the $x – 1$ and then we shall place a new substitution; $(x-1, 1)$:

\[ f(x – 1 + f(x)) = x -1 + f(x) \]

Now make the substitution of $x\to x-1+f(x)$

\[ f^2(x – 1 + f(x)) = f(x – 1 + f(x)) + 2(x – 2 + f(x)) \]

Which by (1) implies, $f(x) = 2 – x$

We have one solution, the second case is a bit more fiddly, it requires you to follow a similar argument and produces that $f(x) = x$.

Now, let us look at what we have done and denote some learning points:

• Check if $f(x) = 0$ is a solution.
• Aways start by substituting in (0, 0)
• Look for non-functional expressions and try and make that zero and see if that leads anywhere
• Take pieces of information gathered from above steps and plug into a new substitution, i.e. if you are looking for $f(0)$, then $(f(0), 0)$ and $(0, f(0))$.
• and finally fiddle with substitutions until it produces a solution, or until you come to the fact you have an injection. Be persistent.

A quick note on injections

Injections are funny things, but they can be used to solve many different functional equations quickly. If you arrive at something of the form of: $f(g(\varpi)) = g(\varpi)$ (This is varpi, $\varpi$ is awesome!!). Then you can invoke an injection. This means that then if you have a second equation, make the substitution of $\varpi\to g(\varpi)$ and you have usually solved it.

To dust with the beast

The lesser spotted functional equation sits in its natural habitat soon to be unravelled by the curious mathematician, the mathematician stalks slowly towards the equation… he slowly brings out his substitutions for $a$ and $b = 0$, then pounces and sets $a = 0$, the equation squirms and transforms:

\[ f(0) + 2f(b) = f^2(b) \]

The equation reveals its secrets and quickly transforms back, that didn’t seem to work. Then the mathematician tries to net the creature with $b = 0$, the creature squirms again and transforms into a different form:

\[ f(2a) + 2f(0) = f^2(a) \]

This form seems to produce no new information and it transforms back. The mathematician curses and seems to be mesmerised by the ever so obvious non-symmetric $a$ and $b$, he wonders how to exploit that. He remembers that this has to be a function and spots out of the corner of his eye a darting linear motion from the beast, he tries to see if he can set the $f^2(x)$ to the same thing and cancel them, cutting the legs off the beast, making it easier to deal with. He lets $a = 0$ and $b = n+1$

\[ f(0) + 2f(n+1) = f^2(n+1) \]

Whilst taking hold of that transformed form, he then seizes an $1$ for $a$ and an $n$ for $b$ and pierces them into the beast.

\[ f(2) + 2f(n) = f^2(n+1) \]

He cuts the legs off the transformed forms and jams them together. Producing a difference:

\[ f(n+1) – f(n) = \frac{1}{2}(f(2) – f(0)) \]

He screams in triumphance as he realises that $f(x) = \alpha x + \beta$, plugging it back in he arrives at $f(x) = 2x + \beta$, where $\beta\in\mathbb{R}$, linearising the beast and turning it to dust.

To find out more about functional equations and other IMO maths stuff, I am to be writing more on my blog or if you want to read more about what life is like behind the scenes at IMO, read this.

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Sunday the 3rd, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.