Welcome to the twenty-fifth match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

Nikki Rohlfing – Mathematical card trick

Nikki Rohlfing is a heavy metal roadie turned maths teacher. On twitter he is @heavymetalmaths.

Pupil: “Sir, how did you do that?”

Me: “Magic!”

Yes, that’s how helpful I can be when teaching maths….I probably just ‘multiplied by a clever number 1’, that seems to do the trick for a lot of secondary school maths!

But how about some actual maths/magic combo: here is a trick I learnt a loooong time ago, yet I keep coming back to for its mathematical magic.

This card trick fascinated me as a child, and I remember one week in particular during the summer holidays at my grandad’s house where I investigated a bit more: can I find a way to make it work with more/less cards? Or more iterations of the separating of stacks? etc. I was counting cards for days but got nothing conclusive.

Over the years, I kept thinking about it: part of me was bothered that I couldn’t work it out, but part of me also enjoyed the fact that it was still magical to me (not the actual trick, but the ‘magic’ of the maths behind it!). So here I am, over 20 years later, having another go at cracking the code, and although my maths is frustratingly not up to scratch, I hope to provide some insight at least, and maybe awaken some curiosity!

So to start with, let’s opt for an exhaustive method to confirm it works, that the method shown in the video does indeed always return the required card into the 3^rd place from the top.

I’ll start by labelling the cards 1-8, show the two stacks, and branch off the “yes”/”no” answers to show all possible outcomes.

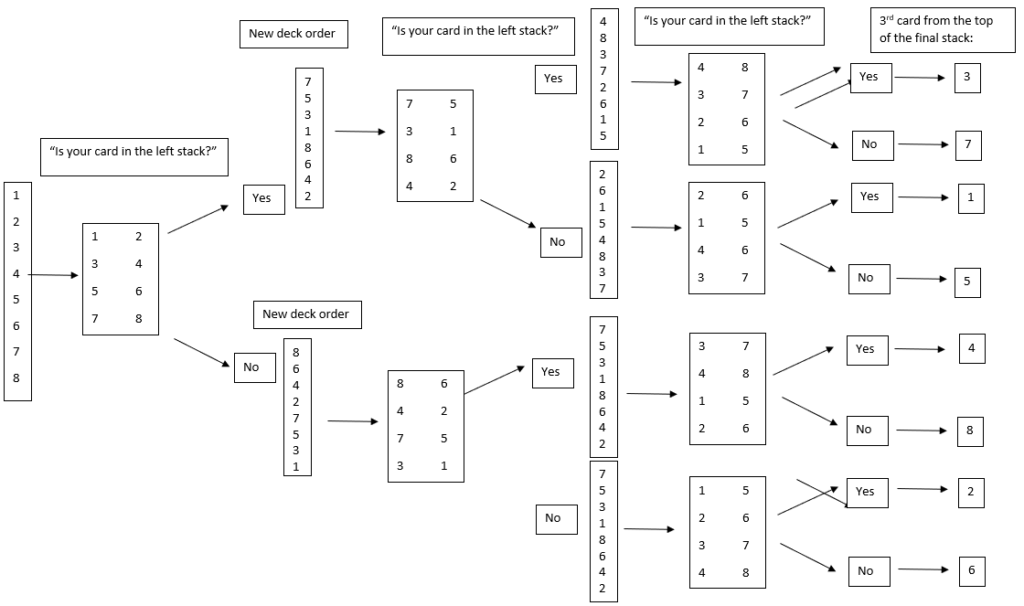
With each “yes/no” decision, you are creating $2\times2\times2=8$ possible outcomes, which is good, as that relates to each of the 8 cards. What was not obvious to me before setting out the diagram was that if going “yes, yes, yes”, the cards are back in the exact order they started in – magic! And looking at the numbers in the stacks, then there’s quite a few patterns to see, like in the second to last, the numbers 1-4 and 5-8 are already grouped together again no matter what route.

But why does putting the stack with the card in on top result in it being always in third place of the final stack?

After not unlocking much myself in the limited time I have, I had a little internet search, and found a Matt Parker video on a very similar (and arguably better) trick. You may want to watch before reading on, as I’ll refer to his method.

The main difference is that Matt’s trick has more cards, and they get divided into 3 stacks, and the similarity is doing the iterative stacking process 3 times. Matt’s trick is based in ternary maths – is this due to doing the process 3 times or because he has 3 stacks? Given his numbering of 0,1,2 to help order the three stacks, I am sensing it’s the latter. This would lead to mine being in binary, which also links in with the $2^3$ cards/choices perhaps.

Matt’s trick is based upon calculating one less than the participants number in ternary form. Given the three stages, this requires 3 digits per number, which then shows why the “one less” is key, as for example, I would need to go from 0 to 7 rather than 1 to 8, so the 3^rd card in the pack would actually be number “2” when counting from 0. Another reason for using 0-7 is that 8 in binary would be four digits, which wouldn’t work. So looking at how the card always lands in 3^rd position, I should perhaps look at the number 2 in binary and try and apply Matt’s method:

\begin{array}{ccc}\\2^2&2^1&2^0\\0&1&0\end{array}

And again, following Matt’s design, I would place the pack with the participants card first on top if I see a 0, and on the bottom if a see a 1, but reading the binary number from right to left. If you have a pack of cards (or by all means try mentally), you might want to think about where the card ends up before clicking on the reveal below.

Spoiler: [peekaboo][peekaboo_content]The card always lands on top…..I actually like this, what a cool variant one could do![/peekaboo_content]

Well, the sharp-minded amongst you will have known this wouldn’t work, as to get it into 3^rd place, I place the stack with the card in always on top. So using the binary method, this would be 000. Hmm, so perhaps I’m computing it wrongly. But, out of interest, what about other numbers? Well, for example, trying “3” (011), gets the card into second place each time, and as you process the binary numbers 0 to 7 you do indeed get all the different positions.

The participants card will move to:

Decimal number 0, binary: 000 $\rightarrow$ 3^rd place

Decimal number 1, binary: 001 $\rightarrow$ 4^th place

Decimal number 2, binary: 010 $\rightarrow$ 1^st place

Decimal number 3, binary: 011 $\rightarrow$ 2^nd place

Decimal number 4, binary: 100 $\rightarrow$ 7^th place

Decimal number 5, binary: 101 $\rightarrow$ 8^th place

Decimal number 6, binary: 110 $\rightarrow$ 5^th place

Decimal number 7, binary: 111 $\rightarrow$ 6^th place

Yet more number patterns, with an odd/even twist. What is also noticeable is how these 0s and 1s link back to the “yes/no” options in my original diagram (although in reverse, and slightly different thinking, but the same underlying principle!).

So looking at the aforementioned 011, means the stack with the participants card in goes (reading right to left) “bottom, bottom, top”, which translates to “no,no,yes” (left to right) in my original notation. It takes the participants card to place 2 in the final stack, which happens to be starting card number 3. In fact, from my diagram, you can see how each binary number 000 to 111 takes card 3, and places it into one of the 8 different places in the pack. This feels like my original trick backwards somehow!

So what has this actually all achieved? Well, two different approaches, working in different directions, using binary and decimal, as well as (perhaps not sensibly) labelling the cards 1-8 when dealing with numbers 0-7….. it has definitely achieved my brain getting muddled a few times!

But one clear break-through is that I now no longer have to rely on revealing the 3^rd card, and can in fact have the participants card pop up anywhere I like! I like this as a possible way to get their card on top, or bottom of the stack, which are key positions for any card magic and could allow an expansion to the routine. The changing of position also allows for greater repetition of the trick without people realising that you just choose the 3^rd card each time.

However, going back to my childhood musings of can this work with more/less cards or iterations, then perhaps I’ve made less progress. Matt’s version shows that at least one more way is possible. But how many different ways could there be? The fact that when you follow my diagram with “yes, yes, yes”, the cards are back in their starting order might be helpful. However, for 3 stacks, like with Matt, I’m not (yet!) sure which combination is required to do the same, given that’s it’s “0/1/2” rather than just “yes/no”. If nothing else, I hope you have a go at doing the card trick with someone; and by all means get in touch if you discover anything I missed!

Pat Ashforth – Some thoughts about becoming a mathematician

Pat Ashforth explores maths through knitting and crochet at woollythoughts.com.

Reading all the pitches in the The Big Lock-Down Math-Off made me start thinking about what influences turn a person into a mathematician or, more specifically, into a particular kind of mathematician.  We all know that there is no dividing line between mathematicians and non-mathematicians. Everyone has some kind of mathematical thinking whether they regard it as maths or not.

I don’t remember much about my maths education in my early life. My father, who was in no way a gambler, taught me to play pontoon when I was old enough to hold the cards and this could have contributed to being at ease with numbers. At the age of three I was one of those awful children who did not ‘rest’ in the afternoon (or sleep much at night either).  I went to a nursery where the other children did rest so, each afternoon, I was sent to the end of the road where I could see the town clock and told to come back at a particular time. I’m not sure I could tell the time properly but I was able to come back and demonstrate, with outstretched arms, the time on the clock. It wouldn’t happen these days.

In Junior School I loved sums, which were more complicated than they are today because we worked in pounds, shillings and pence, and pounds and ounces, and feet and inches. Using several different number bases was just what we did.  There were other lovely things like hundredweights and tons, and pints and gallons.

At the age of eleven I went to the very new local Grammar School. Maths was a revelation and a very different animal from what we have today. It was split into three separate subjects, each with a different teacher – Arithmetic, Algebra and Geometry. I doubt if I had even heard these words before. I remember very little about arithmetic and algebra but geometry had a massive impact. Mr Parkes was terrifying. He was ex-army with the loudest voice imaginable. He always wore a gown. Most Grammar School teachers did in those days. He marched down the corridors and it billowed around him. He had metal tips on the heels of his shoes. That wasn’t unusual either but he seemed to be louder than anyone else. You always knew when he was coming and could get out of the way.

The very first lesson has stuck with me forever. We all had the obligatory geometry set but this didn’t fulfil all of his requirements. Pencils! Two 2H pencils were essential. It was a punishable offence not to have them. On reflection, it makes perfectly good sense. It is not possible to draw a thick line with a 2H pencil and he frequently reminded us that a line, theoretically, has no thickness. The second pencil had to be cut in half. One half was to be used in compasses. We all know how frustrating it is to draw a circle with a bump in it where the pencil hit your fingers. It was all terrifying but it was new and it was fun. To this day every drawing I do has incredibly faint lines and I still feel guilty if I don’t use a 2H pencil to do it.

I loved Maths but I also loved crafts. I wasn’t allowed to do any practical subjects. I was in the stream that had to do Latin instead. I resented that at the time. It was assumed that only boys would do Maths and that they would all be scientists. I was not a scientist. At A Level I wanted to do Maths and English plus something else. This didn’t fit with the school’s Arts/Science paths. To their credit, they rejigged the sixth form teaching to make it possible. Once it became an option I wasn’t the only girl doing Maths. I’m sure my future would have been very different if I had been forced down the science route.

Over time, more by chance than intention I found my own weird way of combining maths and art. I am now very thankful that I didn’t do anything arty in school. I was not directed by other people’s ideas.  I was definitely a geometer and I lay that at the feet of Mr Parkes. You can never know the long term effects of the little things you say and do with students.

So, which bit of maths made you say “Aha!” the loudest? Vote:

 Loading ...

The poll closes at 9am BST on Monday the 1st, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lockdown Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.