Andrew Stacey: I have a confession to make that would probably get me thrown out of every respectable Mathematics Society – were I to belong to one.

I am not a fan of the Fibonacci sequence.

Neither am I keen on the golden ratio. It’s not even transcendental.

It’s not really their fault, it’s just that they get levered in everywhere whether they belong there or not. Particularly in discussions of nature and beauty, and this is exemplified by that ridiculous origin story. We’ve been subjected to a variety of bizarre origin stories over the years (cough radioactive spider cough) but the rabbit story is another level of bizarre.

So I was intrigued, and then delighted, when one of my students, who is a bee enthusiast, told me about a genuinely natural occurrence of the Fibonacci sequence in the ancestry of bees.

I’ll let her take up the story.

Kitty Knight: In a colony of bees there is a single matriarch, the queen bee, who produces all the male and female offspring in the colony. She mates once in her life, when she collects sperm from a number of male bees from other colonies. Back in the beehive, every time she lays an egg she has a choice of whether to lay a female or a male egg, and does this by either laying a fertilised or an unfertilised egg. A fertilised egg will grow into a female bee, and will have half the queen’s DNA, and half DNA from one of the males she originally mated with – that is, the female offspring will have two parents. An unfertilised egg will only have DNA from the queen, and will grow into a male bee, with half the DNA of the females, and only one parent.

The result of this is that males have one parent, a mother, whilst females have two parents, a mother and a father. Looking at the ancestry of a single male bee then yields more interesting results than humans. The male in question will have one mother (generation of size $1$). His mother will then have both a mother and a father (meaning this generation is of size $2$), but this father will only have one female parent whilst the mother will have both a female and a male parent (making a generation of size $3$). The next generation will then be the parents of $2$ females ($4$ parents) and the parent of one male ($1$ parent), making a generation of size $5$. Our single original male therefore has $1$ parent, $2$ grandparents, $3$ great grandparents, $5$ great-great grandparents, then $8$, $13$, $21$, $34$, $55$, $89$ … that is, his number of ancestors follows the Fibonacci sequence (where he is the first in the sequence).

This makes sense, as every generation will consist of a number of females, and a number of males. The number in the generation above will be $\mathrm{females} \times 2 + \mathrm{males}$, as the females have two parents and the males one. The number of females in the current generation is equal to the total number of bees in the generation below (as every bee, male or female, in the generation below must have $1$ and only $1$ female parent). Therefore, the total number of bees in the next generation is the number in the current generation $+$ the number in the previous generation – i.e. the next in the sequence is calculated by summing the two previous terms in the sequence. This method results in the Fibonacci sequence, provided the first two terms are $1$ – and in this case, they are (the original male and his single mother).

The diagram below shows how each of the numbers in each generation are derived from the one below, where $D_{n}$ is the number of drones in the $n$th generation, $Q_{n}$ the number of queens, and $A_{n}$ the total number of bees.

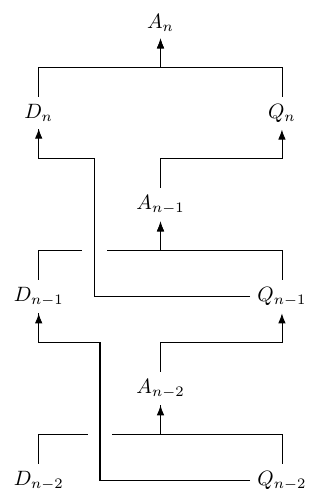
So in equations, we have:

\begin{align}
A_{n} &= D_{n} + Q_{n} \\
&= Q_{n-1} + A_{n-1} \\
&= A_{n-2} + A_{n-1}
\end{align}

Revealing the Fi-Bee-onacci sequence itself.