This is the second in a series of guest posts by David Benjamin, exploring the secrets of Pascal’s Triangle.
Sequences in the diagonals
There are many sequences of numbers to be found in Pascal’s triangle. The Natural numbers occur in the second diagonal, running in either direction, and the next two diagonals after that contain other important sequences:
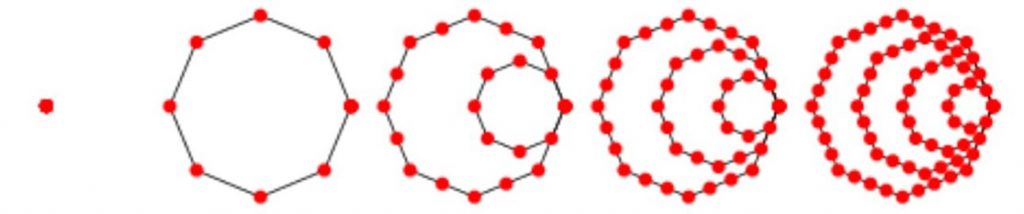
The triangular numbers are part of the sequence of polygonal numbers, all of which can be displayed geometrically by a series of dots. All sets of polygonal numbers begin with $1$ – representing the degenerate polygon, which isn’t really a polygon.
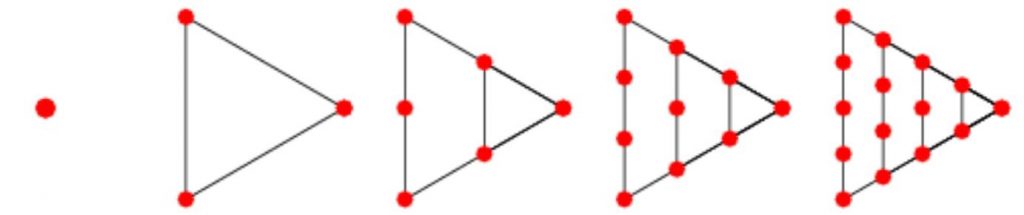
The third diagonal in Pascal’s triangle contains the set of triangular numbers.
Two congruent right-angled triangles can be joined to create a square. In a similar way, summing successive pairs of triangular numbers creates the set of square numbers and so the sequence of square numbers can also be considered to be contained in the third diagonal.
{$1 + 3, 3 + 6, 6 +10, 10 +15, 15 + 21,…$} = {$1, 4, 9, 16, 25, 36,…$}
Yang Hui discovered the formula to find the sum of the triangular numbers. The $nth$ term for the sequence is $\frac{n(n+1)}{2}$ and the sum of the first $n$ terms is $\frac{n(n+1)(n+2)}{6}$, where each term or sum is found by substituting $n = 1, 2, 3, 4,..$
More Square numbers
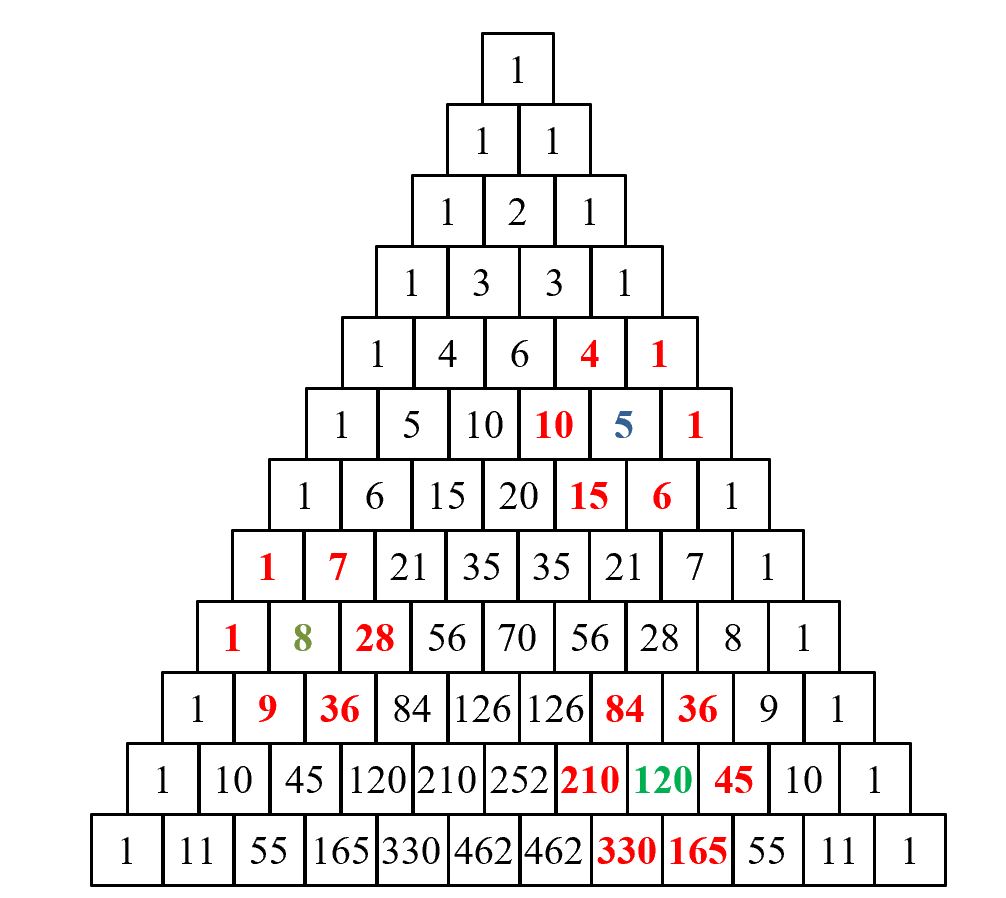
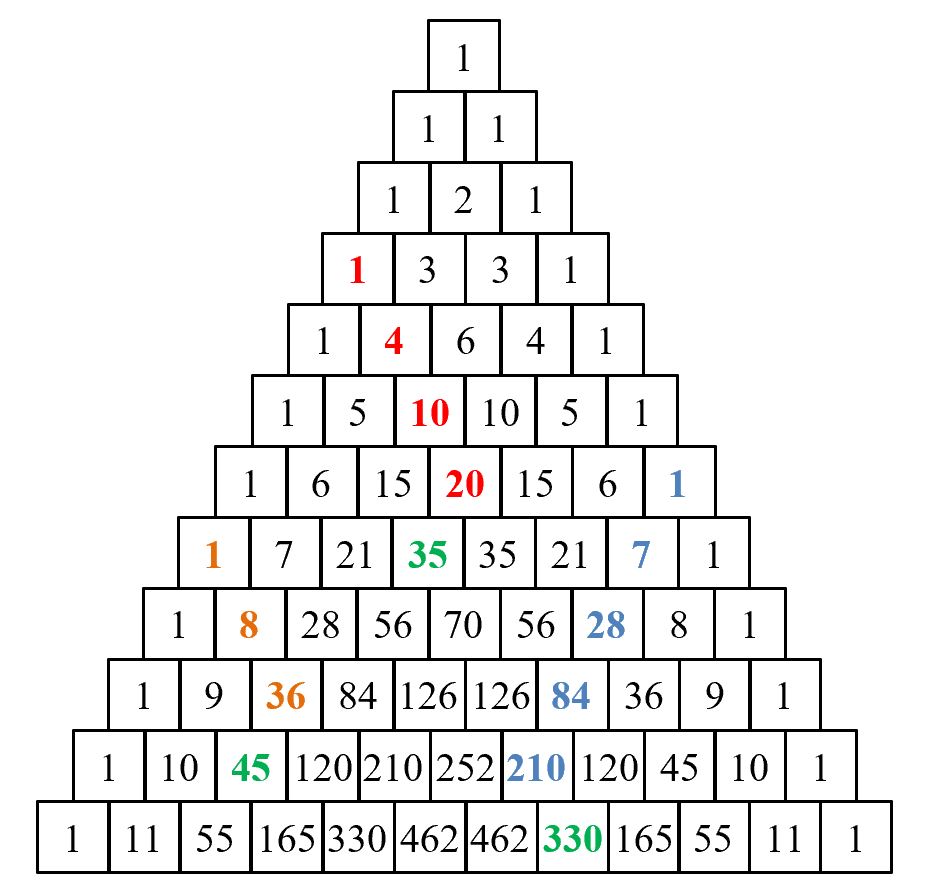
Square numbers can also be found in the triangle by calculating the product of the six numbers surrounding any internal number:
$4\times 1\times 1\times 6\times 15\times 10=3 \hspace{0.1cm} 600=60^2$
$84\times 210\times 330\times 165\times 45\times 36=1 \hspace{0.1cm} 556 \hspace{0.1cm} 006 \hspace{0.1cm} 760 \hspace{0.1cm} 000=1 \hspace{0.1cm} 247 \hspace{0.1cm} 400^2$
$1\times 7\times 28\times 36\times 9\times 1=63 \hspace{0.1cm} 504=252^2$
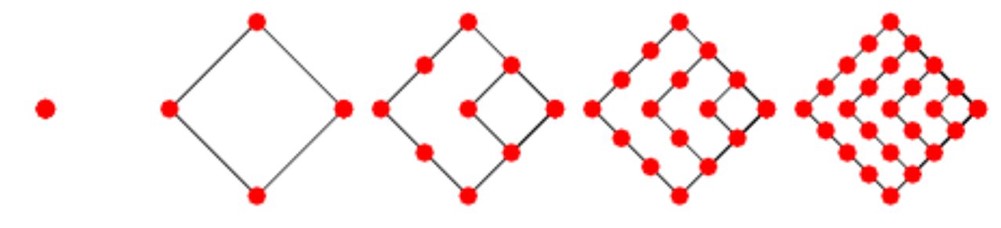
Higher dimensional numbers
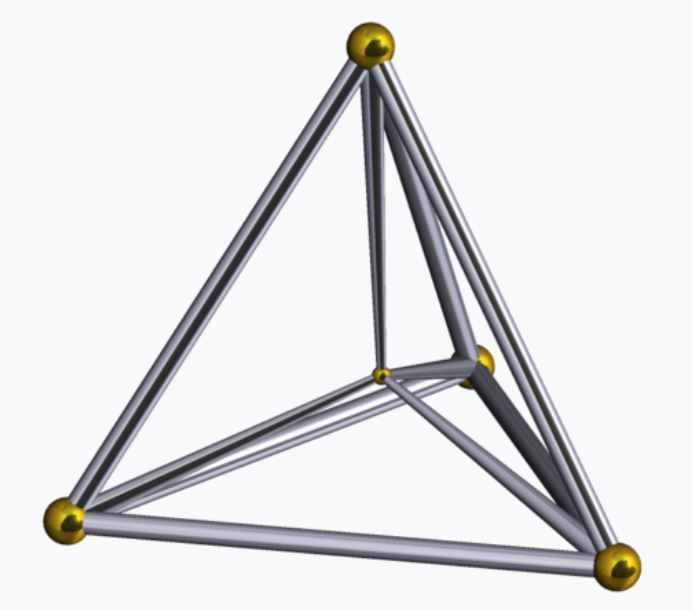
The fourth diagonal of the triangle contains the sequence of tetrahedral numbers, part of the set of pyramidal numbers. They can be represented in 3 dimensions and are created from the triangular numbers.
$1$ on top with $3$ underneath, then $6$, then $10$,….They are displayed below as a stack of balls representing a triangular-based prism. They can also be generated by the power series $\displaystyle\frac{x}{(x-1)^4}=x+4x^2+10x^3+20x^4+35x^5+56x^6+…$. Conway and Guy in their wonderful book, The Book of Numbers, wrote that the tetrahedral numbers are all even except every fourth one, which is odd.
The fifth diagonal of the triangle contains the pentatope numbers: $1, 5, 15, 35, 70, 126, 210,..$ Pascal called them the triangulo-triangular numbers. Pentatope numbers are the sums of the tetrahedral numbers which are the sums of the triangular numbers. The $nth$ term for the sequence is $\frac{n(n+1)(n+2)(n+3)}{24}$ which tells us that the product of four consecutive numbers is divisible by $24$. The power series to generate them is $\frac{x}{(x-1)^5}=x+5x^2+15x^3+35x^4+70x^5+126x^6+…$.
Wolfram Mathworld describes the pentatope as the simplest regular figure in four dimensions, representing the four-dimensional analog of the solid tetrahedron. It is also called the 5-cell, since it consists of five vertices, or pentachoron. The pentatope is the four-dimensional simplex.
The power series $\frac{x}{(x-1)^n}$ generate the diagonals of Pascal’s triangle for $n=1,2,3,4,5,…$
Some other patterns
In Part 1 we saw that the numbers in each row sum to the powers of $2$. If we concatenate the numbers in the first five rows of the triangle then we obtain the powers of $11$:
| $1 = 11^0$ |
| $11 = 11^1$ |
| $121 = 11^2$ |
| $1331 = 11^3$ |
| $14641 = 11^4$ |
Now with some reverse concatenation and summing some pairs of digits we obtain further powers…
$1 5 10 10 5 1 \rightarrow 1 (5 + 1) (0 + 1) 0 5 1 \rightarrow 161051 = 11^5$
$1 6 15 20 15 6 1 \rightarrow 1 (6 + 1) (5 + 2) (0 + 1) 5 6 1 \rightarrow 1771561 = 11^6$
$1 7 21 35 35 21 7 1 \rightarrow 1 (7 + 2) (1 + 3) (5 + 3) (5 + 2) 1 7 1 \rightarrow 19487171 = 11^7$
$1 8 28 56 70 56 28 8 1 \rightarrow 1 (8 + 2) (8 + 5) (6 + 7) (0 + 5) (6 + 2) 8 8 1$
Working from the right, adding the brackets and carrying any $10$ as a $1$ to the sum of the next bracket yields
$214 \hspace{0.1cm} 358 \hspace{0.1cm} 881 = 11^8$
Primes and Pascal
When the second number in each row is a prime number, the symmetry of the triangle means the penultimate number in that row is the same prime and it turns out that all the numbers between the two primes are multiples of that prime.
$55 = 5 \times 11$, $165 = 15 \times 11$, $330 = 30 \times 11$, $462 = 42 \times 11$
We conclude Part 2 with the finite hockey stick sequences:
Start with any $1$ and move down the diagonal any number of rows. The sum of those numbers is equal to the number on the next row on the reverse diagonal
$1 + 4 + 10 + 20 = 35$, $1 + 7 + 28 + 84 + 210 = 330$, $1 + 8 + 10 + 36 = 45$.
In the next part, we’ll consider another famous sequence with an unexpected connection to Pascal’s triangle – the Fibonacci numbers.





Some remarkable discoveries are uncovered here:
The product of the six numbers surrounding any internal number produces a square number!
I particularly liked how power series are used to generate the diagonals of Pascal’s triangle
The concatenation section is astonishing albeit slightly mind-boggling!
Multiples of the prime they are sandwiched between & Hockey stick sums – all v surprising.
Interesting
How can I explain in a meaningful way to my curious 3rd and 4th graders that the numbers 1,5,15,35,70 in Pascal’s triangle are higher dimensional number ? I got so far saying the 1s along the edge are points or zero dimensional ,the 1,2,3…are all linear or 1 dimensional ,the triangle numbers are two dimensional and the Tetrahedral numbers are three dimensional. So good so far, this makes sense to my students , We would now continue to call the Pentatope numbers 4 dimensional , or a 4 dimensional kind of Tetrahedron ,but is there away to see this and understand it, not only for the students but for the teacher too. Thank you Peter
Hi Peter – perhaps use a parallel explanation. I used to introduce higher dimensions via nodes and edges. Joining 2 nodes to create a line. Join correspopnding nodes of 2 lines to create a square, joining the nodes of 2 squares to create a cube, then 4D-cube,….Images here: https://n-dimensional.de/cubes/ I would then extend to show and discuss Escher images and Julian Beever’s pavemnt art https://www.julianbeever.net/pavement-art-3d-illusions/ Some students would inevitably argue that 4D-cubes don’t exist but I would counter that with lines don’t exist they are only in the mind. And then there is Flatland https://www.youtube.com/watch?v=avMX-Zft7K4 a video of Flatland, A Romance of Many Dimensions, a satirical novella by the English school teacher Edwin Abbott Abbott
David, thank you so much for your reply . Especially for the link to visualize a 4D cube is very helpful with regards to my question.
My students and I can learn a lot from your article about Pascal’s triangle. I was always intrigued by the fact that in case the row is prime all its entries except the 1s are divisible by the row number. My enthusiastic students use this fact in connection with discovering , learning and practicing divisibility rules when it comes to the numbers along the larger row numbers. It is certainly tempting to conclude that when all entries in a row are divisible by the row number that the row number must be prime, which is true for the few cases we could test (The entries get so large. The largest number in row 19 is already 92,378) and just as that one all others are divisible by 19 too. and yes 19 is prime . And yet it’s not always true that when all entries are divisible by the row number, that the row number is prime . Is not row 341 a notorious counter example?
Thank you
Peter