Guest author David Benjamin shares some of his favourite ways to use sequences in a teaching context.
As a maths teacher, I’ve found that sequences are a great way to engage and inspire mathematical reasoning. I thought I’d share some examples of sequences, and sequence-related activities, I’ve used with success in the past.
A simple starter
Whenever I asked a group of students for the next 3 terms in the sequence $2,4,6$, I expected their responses to be $8,10,12$. I always hoped to find a budding Carl Gauss who would say $12,24,36$ and then explain that $2,4,6,12,24,36$ are the $2^{nd}$ to $7^{th}$ terms of the sequence of integers that are the product of two factorials, with first term $1$.
In fact the wonderful On-Line Encyclopaedia of Integer Sequences displays $5508$ sequences containing the subsequence $2,4,6$, which opened up a discussion about the need for more information – a starting number, a rule that defines how the next term is generated, and so on. Entering more terms reduces the number of results – $2,4,6,8,10,12$ brings up a possible 337 sequences, such as the product of decimal digits of n (can you work out where this set of terms starts within the sequence without looking?).
Of course, not all sequences have a rule to give the next term – the set of prime numbers being a prime example, or the next digit in the sequence of decimal digits in any irrational number. Many of the examples of sequences students may encounter are arithmetic or geometric progressions, and they’re expected to derive the rule, or give the next in the sequence – but it’s useful for them to see examples of sequences of different kinds, including ones which don’t have a simple pattern.
Sequences in $\pi$
One lesson starter I used was to search, using the Pi-Search page at angio.net, for students’ birthdays in $\pi$. A mini competition to see which student’s birthday appeared the most times, the closest to the start or the furthest away from the decimal point in the first 200 million digits. A starting point was my own birthday 18/11/1952, which produces the following result:
The current record for the number of digits of $\pi$ is 62.8 trillion
![Screenshot of the angio.net Pi Search, with plain text on a pink background. Text reads: 'The string 18111952 occurs at position 25115087. This string occurs 2 times in the first 200M digits of Pi.
counting from the first digit after the decimal point. The 3. is not counted.
[ Find Next button ]
The string and surrounding digits:
30362263315144765995 18111952 13047386731114123205'](https://aperiodical.com/wp-content/uploads/2022/08/18111952-1024x309.jpg)
I used the same website as a plenary after a lesson on common sequences:
| Fibonacci: $11235813$ occurs at position $48300974$ |
| Triangular numbers: $1361015$ occurs at position $5505126$ |
| Primes: $23571113$ occurs at position $8157777$ |
This often led into a philosophical discussion about the longest possible length of a string of an irrational number inside itself, or inside another irrational. How much of $\pi$ is in $\pi$?, $e$ is in $\pi$?, $\pi$ is in $e$,…?


The Collatz conjecture
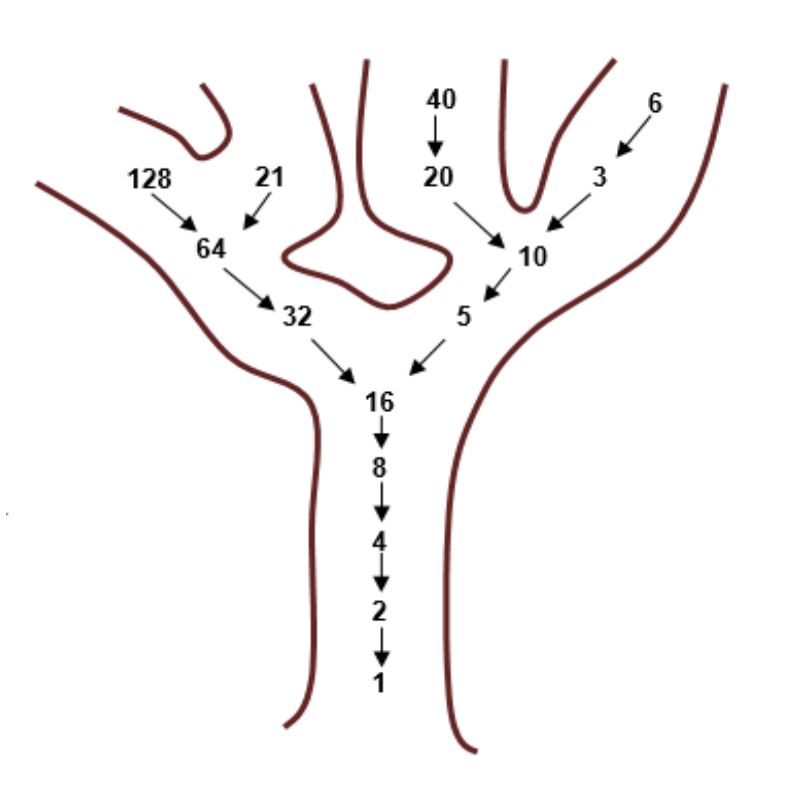
Lothar Collatz [1910-1990] was a German mathematician most famous for his eponymous and currently unsolved conjecture on the outcome of the infinite number of sequences generated from any positive integer, $n$. If $n$ is even then halve it to obtain the next number in the sequence, if $n$ is odd, the next number is found by multiplying by $3$ and adding $1$.
Below is the sequence generated when $n=17$.
$17 \rightarrow 52\rightarrow 26\rightarrow13\rightarrow40\rightarrow20\rightarrow10\rightarrow5\rightarrow16\rightarrow8\rightarrow4\rightarrow2\rightarrow1\rightarrow4\rightarrow2\rightarrow1$
If the rule for odd numbers is changed to ‘multiply by $3$ and subtract $1$, then there appear to be 3 different endings to a sequence: $1,2,1,2$ or $5,14,17,20,10,5$ or the easily missed $17,50,25,74,37,110,55,164,82,41,122,61,182,91,$$272,136,68,34,17$
The conjecture is that all such sequences end at $1$ [via the loop $4,2,1$]. The sequence is often referred do as the hailstone sequence, since the value of the numbers generated bounce up and down as hailstones do in a cloud. Paul Erdős [1913-1996], the Hungarian mathematician and problem solver, believed mathematics was not ready for such a problem and John Conway stated in this lecture that it would not be solved in his lifetime – sadly, this is now true. At the time of writing the conjecture has been verified for all positive integers up to $2^{68}=295147905179352825856$ or 295 quintillion 147 quadrillion 905 trillion 179 billion 352 million 825 thousand and 856.
The number of steps to reach 1 for $n=1$ to $10$ are displayed in the table below:
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| Steps | $0$ | $1$ | $7$ | $2$ | $5$ | $8$ | $16$ | $3$ | $19$ | $6$ |
I used the Collatz sequence in mathematics clubs – a sequence not in KS3/4 specifications and a way of stretching students horizontally. It also allowed me to introduce them to the concept of inverse functions by creating a ‘hailstone tree’. One of my classroom walls displayed a very large student-created tree with trunk $16,8,4,2,1$ and with the first branches appearing at $16$. Students would often extend the tree before the start of a lesson, leaving me to check for any errors later in the day! I hope the image of the tree has remained in some students’ minds in the same way I can still visualise the digits of $\pi$ looping round 3 walls in one of the classrooms at the secondary school I attended in Burnage, Manchester.
John Conway’s constant, $\lambda$
Many years ago a student challenged me to find the next few terms of this sequence $1, 11, 21, 1211,…$. I failed. He gave me the next 4 terms $111221, 312211, 13112221, 1113213211,…$ but that didn’t help. I felt better when I found out that Conway was also unable to work out the sequence when shown it by one of his students at Cambridge University. But the great man was able to analyse what is now called the look-and-say sequence or the C-sequence – another sequence I used in mathematics clubs – and of course Conway took the sequence to a whole new level.
- $1$ is “one one” or $11$
- $11$ is “two ones” or $21$
- $21$ is “one two and one one” or $1211$
- $1211$ is “one one, one two and two ones” or $111221$
- …
Even when the ‘rule’ is known it’s still a challenge of concentration to find more terms (given in the OEIS entry for A005150). Well, it is for me!
Conway’s analysis of the sequence led him to the constant $\lambda$ which is calculated in a similar way to how the golden number $\phi$ is calculated from the Fibonacci sequence:
If $L_{n}$ is the number of digits of the $n^{th}$ number of the sequence then
$\lambda=\displaystyle\lim_{n\to \infty} \frac{L_{n+1}}{L_{n}}\approx1.303577269034…$, an algebraic number, specifically the unique positive real root of this polynomial of degree 71:
\[x^{71}-x^{69}-2x^{68} -x^{67}+2x^{66}+2x^{65}+x^{64}-x^{63}-x^{62}-x^{61}-x^{60}-x^{59}+2x^{58}+5x^{57}\]\[+\ 3x^{56}-2x^{55}-10x^{54}-3x^{53}-2x^{52}+6x^{51}+6x^{50}+x^{49}+9x^{48}-3x^{47}-7x^{46}-8x^{45}\]\[-\ 8x^{44}+10x^{43}+6x^{42}+8x^{41}-5x^{40}-12x^{39}+7x^{38}-7x^{37}+7x^{36}+x^{35}-3x^{34}+10x^{33}\]\[+\ x^{32}-6x^{31}-2x^{30}-10x^{29}-3x^{28}+2x^{27}+9x^{26}-3x^{25}+14x^{24}-8x^{23}-7x^{21}\]\[+\ 9x^{20}+3x^{19}-4x^{18}-10x^{17}-7x^{16}+12x^{15}+7x^{14}+2x^{13}-12x^{12}-4x^{11}-2x^{10}+5x^9\]\[+\ x^7-7x^6+7x^5-4x^4+12x^3-6x^2+3x-6=0\]
The image below gives the ratio $\displaystyle\frac{L_{n+1}}{L_{n}}$ for $n=7$ to $n=12$:

Conway explains the results of his analysis of the sequence in this video.
Some more activities
Here are some more activities on ‘unusual’ sequences I’ve used in the classroom.