This is a guest post by David Benjamin, who’s previously written several other guest posts on various topics.

It’s unavoidable that part of doing mathematics will always involve arithmetic: the simple calculations, additions and multiplications that so much else is built on. But the beauty of mathematics is that even these basic operations can be performed in a multitude of interesting ways.

For example, multiplication, division and subtraction of whole numbers can all be done using forms of addition. Many of us were taught to subtract using the ‘borrow and pay back’ method, but I much prefer to use addition, especially when subtracting numbers in my head. For example, to calculate $63-17$:

\[17 \rightarrow + 3 \rightarrow 20 \rightarrow + 43 \rightarrow 63\]

Then

\[63\ – 17 = 3 + 43 = 46\]

This video by Howie Hua (also available on Twitter) includes this method, which he calls ‘friendly jumps’, alongside some others for making subtraction less of a chore:

In this article, we’ll explore various methods for multiplying whole numbers – simple methods used in the school classroom, ones with historical connections and even ones which tie into modern computing.

The grid method for multiplication

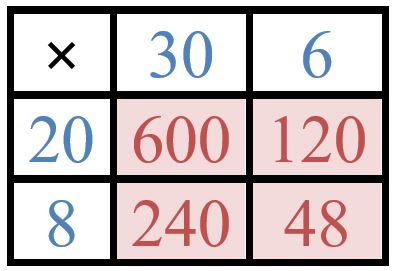
When teaching mathematics I chose to introduce my students to the grid method for multiplication – and many students preferred to use it over other methods. The grid provides links to the partition of numbers, to the area of rectangles and demonstrates to students why the method works. It also proved useful when moving on to the expansion of a pair of binomials like $(x+4)(x+2)$ and subsequently the factorisation of quadratic functions.

\[36 \times 28\equiv (30 + 6) \times (20 +8) = 600 + 120 + 240 + 48 = 1008\]

Grid multiplication, as with Pythagoras’ theorem, is based on area. The rectangle with length $36$ units and width $28$ units is split into four smaller rectangles: $30$ by $20$, $30$ by $8$, $20$ by $6$ and $8$ by $6$. The area of each of these smaller rectangles is easier to calculate using mental arithmetic than the area of the original rectangle. Grid multiplication is a method believed to have been widely used in India around the 10$^{th}$ century and introduced to Europe, along with the Hindu-Arabic digits we use today, by Fibonacci at the start of the 13$^{th}$ century.

Once students become proficient with the the grid method, they are able to go straight to

\[49 \times 56 \equiv (40 +9)\times (50+6)=2000+240+450+54=2744\]

The grid method can also be used to multiply mixed numbers like $2\frac{1}{3}\times1\frac{2}{3}\equiv(2+\frac{1}{3})(1+\frac{2}{3})$. But I wouldn’t recommend it!

Napier’s Bones

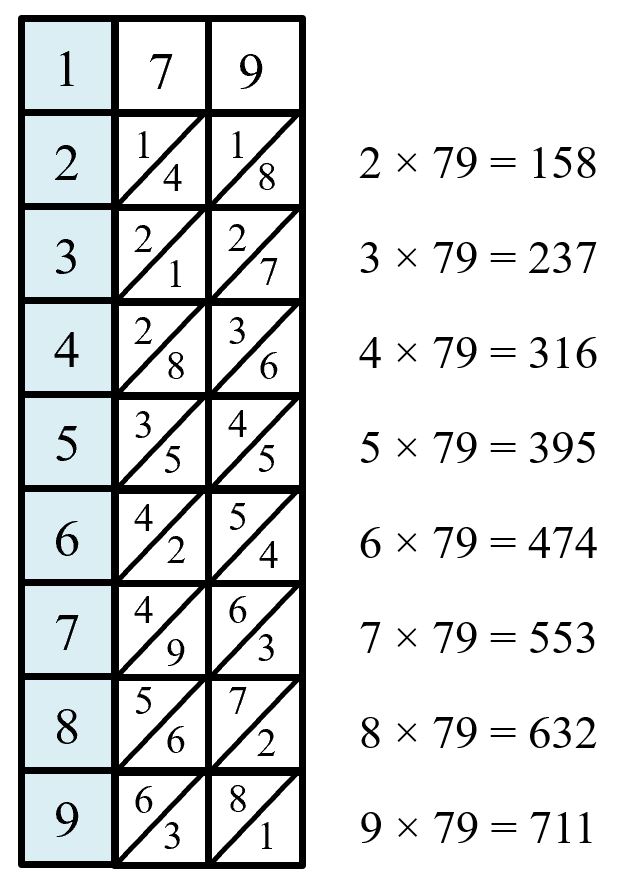
John Napier [1550-1617] was a Scottish amateur mathematician who is best known for his invention of logarithms and numbering rods. The rods were made of ivory, looked like bones and hence became known as Napier’s bones. They can be used for multiplying, dividing and calculating square and cube roots.

My dad was a cabinet maker and made me a set in wood – and left me with the more difficult task of adding the digits. The bones, like logarithms, reduces multiplication to addition and division to subtraction. In the classroom, creating their own set of bones helped students who struggled with single digit multiplication.

To create the product, the bones corresponding to the digits of the multiplicand are lined up side by side and the answer is calculated from the digits working from the right in the relevant row. When there are 2 digits in a parallelogram, it is their sum which is used. If that sum is greater than 9, then carry into the next triangle on the left, as in $4\times79$ below:

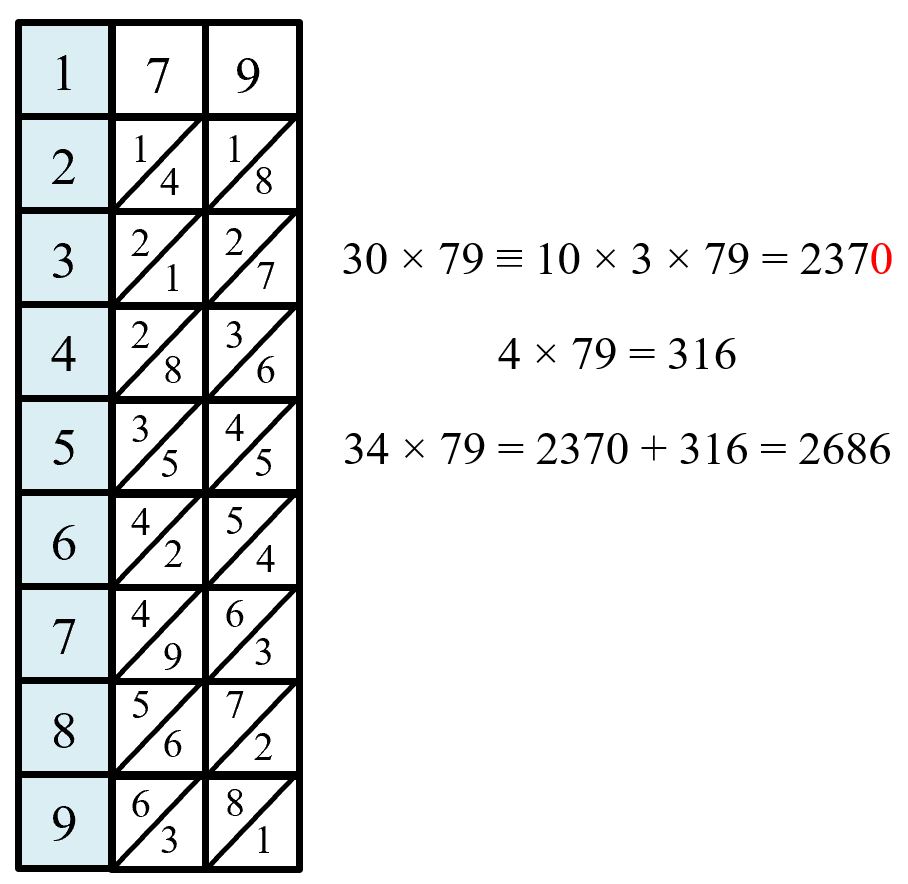
When the multiplier has more than 1 digit then we make use of partition and the distributive law:

$34\times79\equiv(30+4)\times79=30\times79+4\times79$

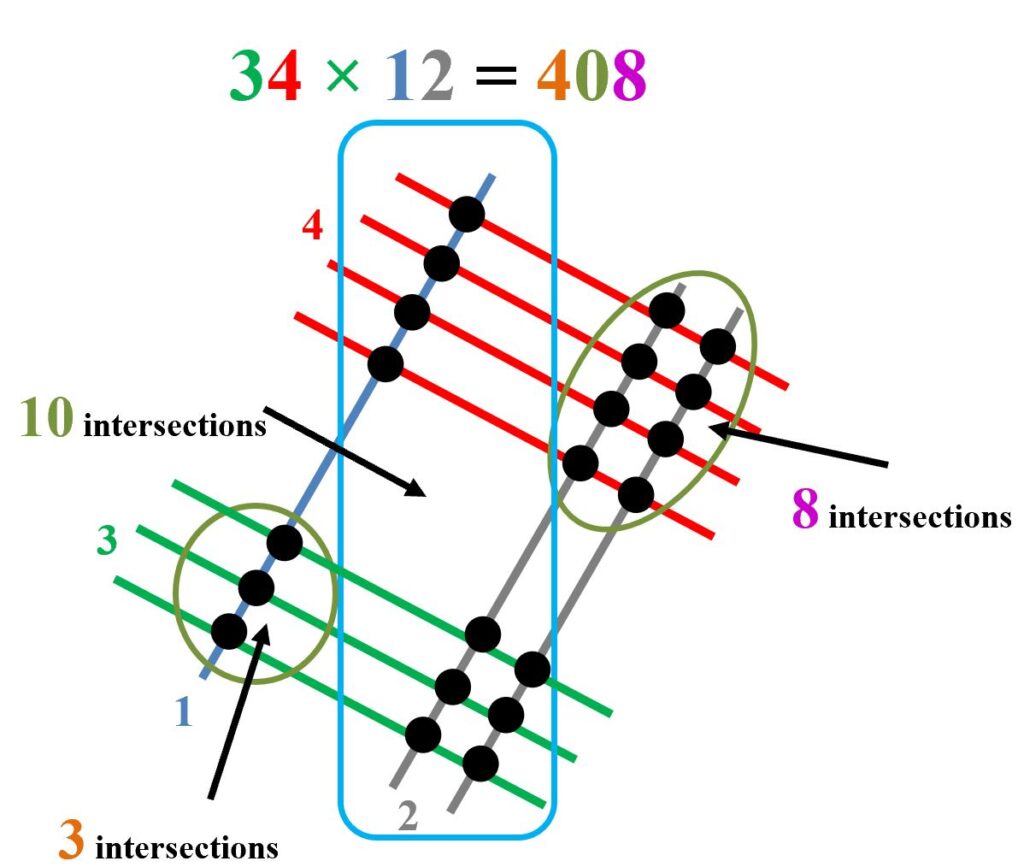
Japanese lattice multiplication

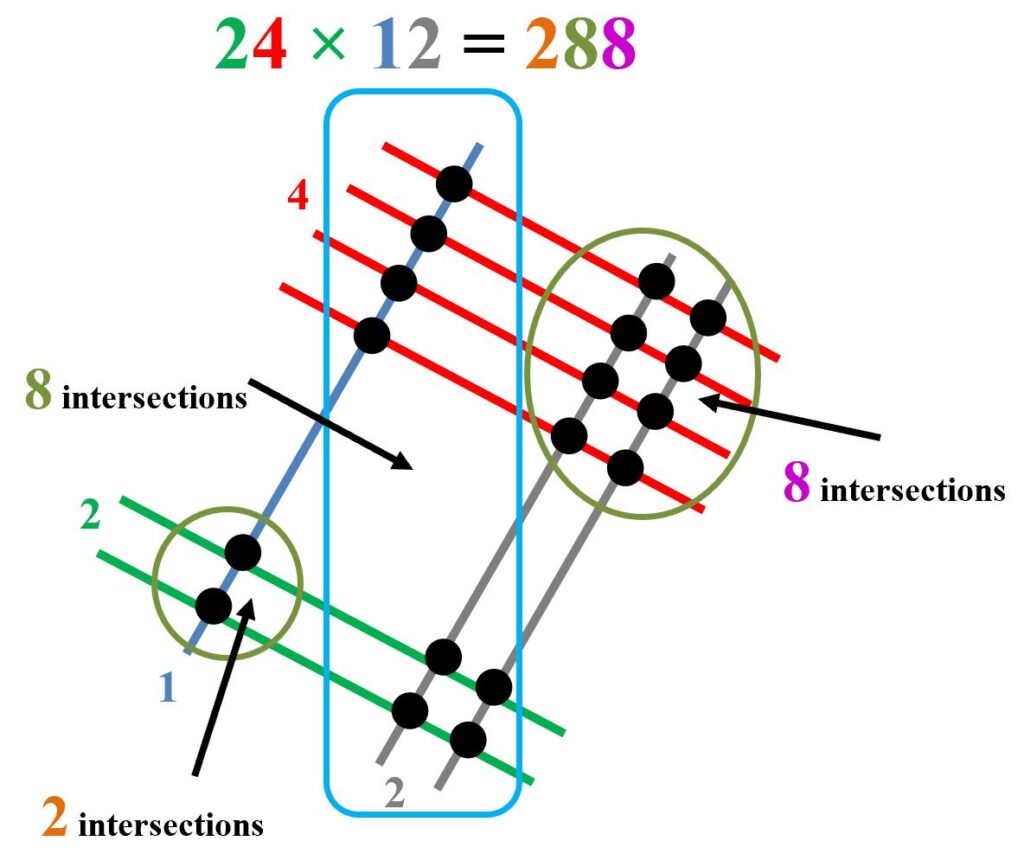
The Japanese multiplication method is based on geometry and was invented by professor Fujisawa Rikitarol (1861-1933) around 1900. Products are calculated by counting the number of intersections of parallel lines. The digits in the multiplier and the multiplicand indicate the number of parallel lines needed.

$24\times12$

The answer is produced from the right by counting the intersections. In the middle area, the value is given by the sum of both sets of intersections. In the example above, two lines meeting four lines creates $2$ lots of $4$ intersections – so the product is $2\times4=8$

$24\times12\equiv(20+4)(10+2)=100\times2+10\times(4+4)+2\times4=200+80+8=288$

If any total is greater than 9, then carry into the next set as shown in the example below

This video by Zero Math demonstrates the method when finding the product of two 3 digit numbers and a second video shows what to do when there are zeros in the numbers being multiplied.

Multiplying numbers close to powers of 10

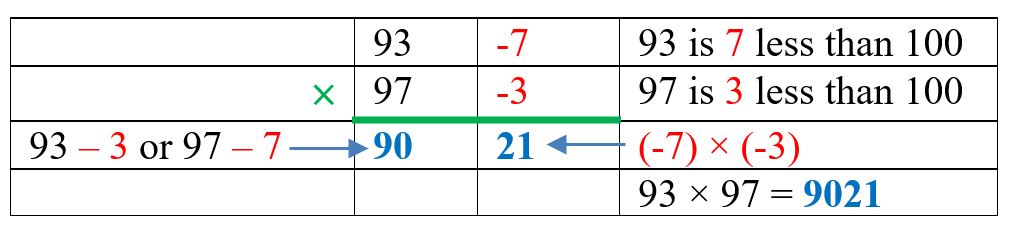
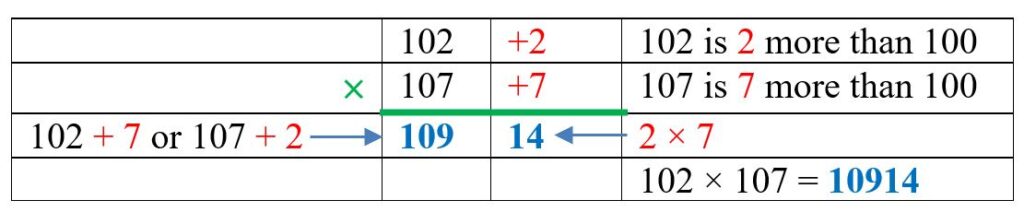
Base multiplication is a Vedic method – a technique from Vedic mathematics – to calculate the product of numbers close to powers of the base (in the case of base $10$, these are $10, 100, 1000,…$). It relies on the Vinculum process, which is a method of writing numbers in which a bar on top of a digit indicates a subtraction, as in the examples below.

\[372\bar{4}=3000+700+20-4=3716\]

\[37\bar{2}4=3000+700-20+4=3684\]

\[7\bar{2}\bar{4}=3000+700-20-4=3676\]

We can use this method to simplify performing subtraction calculations:

\[ \begin{eqnarray}783 & \\ – 348 & \\ \hline \textcolor{blue}{44\bar{5}} & \textcolor{blue}{\ = 440\ – 5 = 435} \end{eqnarray} \]

\[ \begin{eqnarray}614 & \\ – 268 & \\ \hline \textcolor{blue}{4\bar{5}\bar{4}} & \textcolor{blue}{\ = 400\ – 50 – 4 = 346} \end{eqnarray} \]

\[ \begin{eqnarray}19083 & \\ – 1831 & \\ \hline \textcolor{blue}{18\bar{8}52} & \textcolor{blue}{\ = 18000 – 800 + 52 = 17252} \end{eqnarray} \]

This is actually the fourth method shared by Howie in the video above, but using slightly different notation.

Multiplication when both numbers are just less than 100

Multiplication when both numbers are just more than 100

Multiplication when one number is just less than 100 and the other is just more than 100. This example makes use of the Vinculum process

This method of multiplication is only useful when both the multiplicand and the multiplier are close to the power of 10. If, for example, the sum is $56\times49$ then we need to calculate $(-44)\times(-51)$ – a sum not too dissimilar to the original one!

Yavadunam Sutra

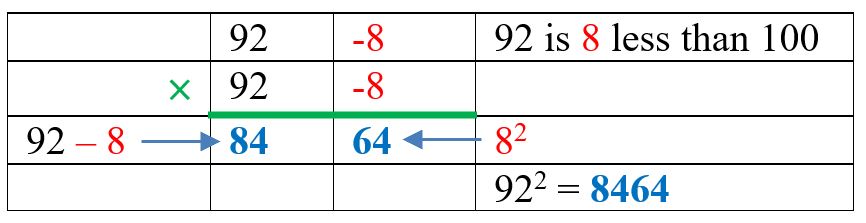
Yavadunam Sutra is a Vedic method to square numbers that are close to a power of 10. It provides a way to square numbers in the head:

$92^2 \rightarrow (92-\textcolor{red}{8})\vert{\textcolor{red}{8}^{2}}\rightarrow84\vert64\rightarrow8464$

$98^2 \rightarrow (98-\textcolor{red}{2})\vert{\textcolor{red}{2}^{2}}\rightarrow{96}\vert{04}\rightarrow9604$

$112^2 \rightarrow (112+\textcolor{red}{12})\vert{\textcolor{red}{12}^{2}}\rightarrow{124}\vert{144}\rightarrow12(4+1)44\rightarrow12544$

There’s more explanation in this TED-Ed talk: The magic of Vedic math – Gaurav Tekriwal

Leibniz and binary numbers

The easiest two numbers to use in multiplication are $1$ and $0$. Gottfried Wilhelm Leibniz (1646-1716) the joint-discoverer of the infinitesimal calculus, liked to use binary numbers for some arithmetical calculations. He even discussed the possibility of designing a mechanical binary calculator which would use moving balls to represent binary digits. The manuscript, written in 1679, is housed in the Gottfried Wilhelm Leibniz, Bibliothek Niedersächsische Landesbibliothek, in Hannover.

The machine was never built, but in 1705 he wrote an Explication de l’arithmétique binaire, qui se sert des seuls caracteres 0 & 1; avec des remarques sur son utilité, & sur ce qu’elle donne le sens des anciens figures Chinoises de Fohy’ which was published in Histoire de l’Académie Royale des Sciences année MDCCIII. An English translation can be found on the Liebniz Translations website. Whilst doing arithmetic is very easy, Leibniz pointed out that working in denary (decimal) is preferable:

However I am not in any way recommending this way of counting in order to introduce it in place of the ordinary practice of counting by ten. For, aside from the fact that we are accustomed to this, we have no need to learn what we have already learned by heart. The practice of counting by ten is shorter and the numbers not as long.

Gottfried Liebniz

Leibniz did eventually build a calculator – the stepped reckoner – completed in 1694. Unlike Pascal’s calculator, it was able to perform multiplication and division as well as addition and subtraction. However, the Reckoner couldn’t carry or borrow numbers automatically and more significantly, it didn’t work. There is one surviving version of the calculator also housed at the National Library in Hannover and a replica is displayed at the Deutsches Museum in Munich.

While Liebniz preferred denary calculations to working in binary, binary numbers do have their uses in other forms of multiplication – as we will see.

Russian peasant multiplication

Sometimes referred to as Russian multiplication, Ethiopian multiplication or Egyptian multiplication, this method makes use of doubling and halving. It’s possible the users knew that this method makes use of binary numbers, but they could not have imagined the technique would be the one that microprocessors would be using centuries later.

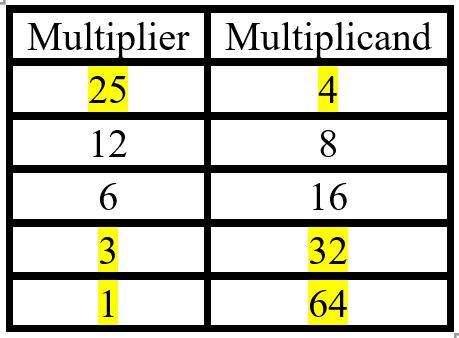
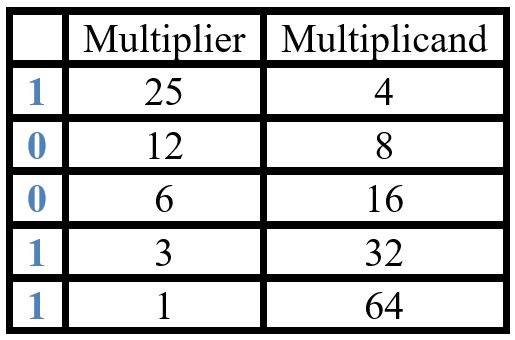
To perform this method, choose a multiplier and a multiplicand. Create a table with a column for each, writing the number at the top of its own column. Then follow this procedure to fill each column:

• Halve the multiplier, ignoring any remainders, and stop at 1
• Double the multiplicand

To extract the answer, highlight the rows containing odd numbers in the first column and sum the corresponding numbers in the second column.

\[25\times4=4+32+64=100\]

Part of the reason this works is that halving a number and ignoring the remainders is one way to turn a denary number into a binary number – each binary digit is the remainder on division by 2, and it is 1 for odd numbers and 0 for even numbers. The binary equivalent of $25$, the multiplier, is written upwards from the bottom of the table, and the rows corresponding to 1s are those we add. In our example, $25$ as a binary number is $11001$.

\[25 \times 4 \equiv (1\times16+1\times8+0\times4+0\times2+1\times1)=(16+8+1)\times4=100\]

Thoughts on teaching and multiplication techniques

It is essential to make students confident with numbers from the beginning of their schooling and to encourage them to suggest alternative ways to solve problems. Not every idea may be suitable but we all learn from methods that do not work and enjoy the thrill of finding the neatest solution to a problem. Understanding arithmetic leads to success with algebra.

Throughout my 44 year career as a teacher of mathematics, I met so many people who told me how they hated mathematics at school and were not confident when using numbers. There came a time when asked what I did, I replied I was a coal miner. It became a way of avoiding hearing experiences of the misery of their mathematics lessons. Manchester City defender, Manuel Akanji had the opposite experience – as he explains in this video, I was interested in numbers at school.

This quote from a research paper on the use Japanese Multiplication in teaching summarises it well:

Mathematics is a vital tool for national development. It is not just a mere subject offered in schools but it is a pillar upon which other discipline depends on. Mathematics has its real-life application in medicine, political science, engineering, construction, computer science, business, fashion designing, cooking and baking –the list is endless. The problem has never been “the role of mathematics but the interest in mathematics”. Students generally express fear, shock, phobia just at the mention of the word mathematics. Getting the students to be interested in learning mathematics has been one of the difficulties teachers of mathematics face. Research has shown that students especially those at the primary level love learning when concepts are visualized. Visualizing concepts triggers the interest of students hence, mathematics teachers are encouraged to make mathematics appealing, admiring, and interesting by visualizing mathematics concepts to the students.

Further reading

The Man Who Loved Only Numbers – Paul Hoffman’s biography of Paul Erdős

Vedic Squares & Vedic Worms, Spirolaterals

National Museums Scotland and Napier’s bones

The Effect of Japanese Multiplication on Pupils Interest in Mathematics