Here’s the third quarter-final match of The Big Internet Math-Off. Today, we’re pitting Fran Watson against Fran Herr. It’s an extravafranza!

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Fran Watson – Learn about rotation

Fran invites you to hum along, join in with the actions or just listen and enjoy!

Fran Watson is a teacher and communicator of mathematics originally hailing from Cornwall but now living in Cambridgeshire (by way of Cardiff in between – locations today brought to you by the letter C!) She loves puzzles, origami, games and musical theatre and will endeavour to weave these passions into her pitches.

Fran Herr – All knotted up

Take a long paper strip, twist one end \(180^{\circ}\), and attach the short ends with some tape. This produces a Möbius loop.

If have spent some time in the math communication world, you might know the result of cutting this shape along the center line. But, if this is new for you, take a moment and try the experiment for yourself! (Or just watch the video below.)

Why do we get only one loop? My favorite explanation is to view the resulting longer loop as a thickened version of the boundary of the Möbius loop. This experiment tells us that the boundary of the Möbius loop is a single unknotted circle.

Consider repeating this process with more twists. For a Möbius loop with \(k\) half-twists, what is the result of cutting it in half? If you want to know the answer in full generality, I made a video on this exact topic a few years ago. I will demonstrate one more example here: a thrice-twisted Möbius loop.

This little activity tells us that the boundary of the thrice-twisted Möbius loop is the trefoil knot. Have I surprised you yet?

A mathematical knot is an continuous embedding of the circle into \(\mathbb R^3\). Think of a piece of string with the ends attached. Two knots are the same (ambiently isotopic) if you can “wiggle them around” in \(\mathbb R^3\) to look the same. We can also have links which are embeddings of a finite disjoint collection of circles into \(\mathbb R^3\). I will often abuse terminology and call them all “knots”. Some of my favorite examples are below.

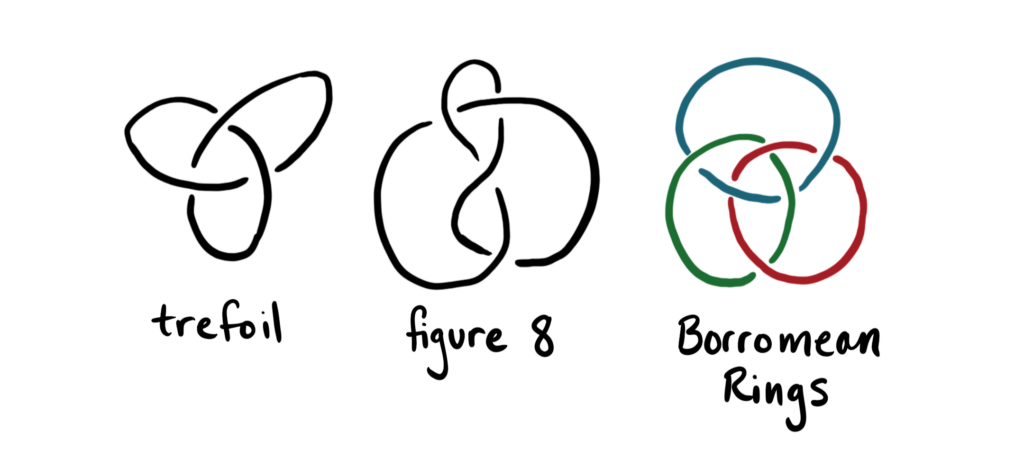
Knots are a bit squirrely in character. For example, mathematicians don’t yet know an algorithm to tell if two knots are the same! One way to study knots is to instead study a Seifert surface of a knot. This is an (orientable) surface with the given knot (or link) as the boundary. Although the “orientable” condition does have some uses, it doesn’t matter for our purposes so we will consider both orientable and non-orientable Seifert surfaces. Our investigation above reveals that the thrice-twisted Möbius loop is a (non-orientable) Seifert surface for the trefoil knot.

Given a knot, there is a simple algorithm to generate a corresponding Seifert surface (two surfaces, in fact). First draw a planar knot diagram which sections the plane into different faces. We can color these faces red and blue in an alternating way so that no two faces sharing a bounding edge are the same color.

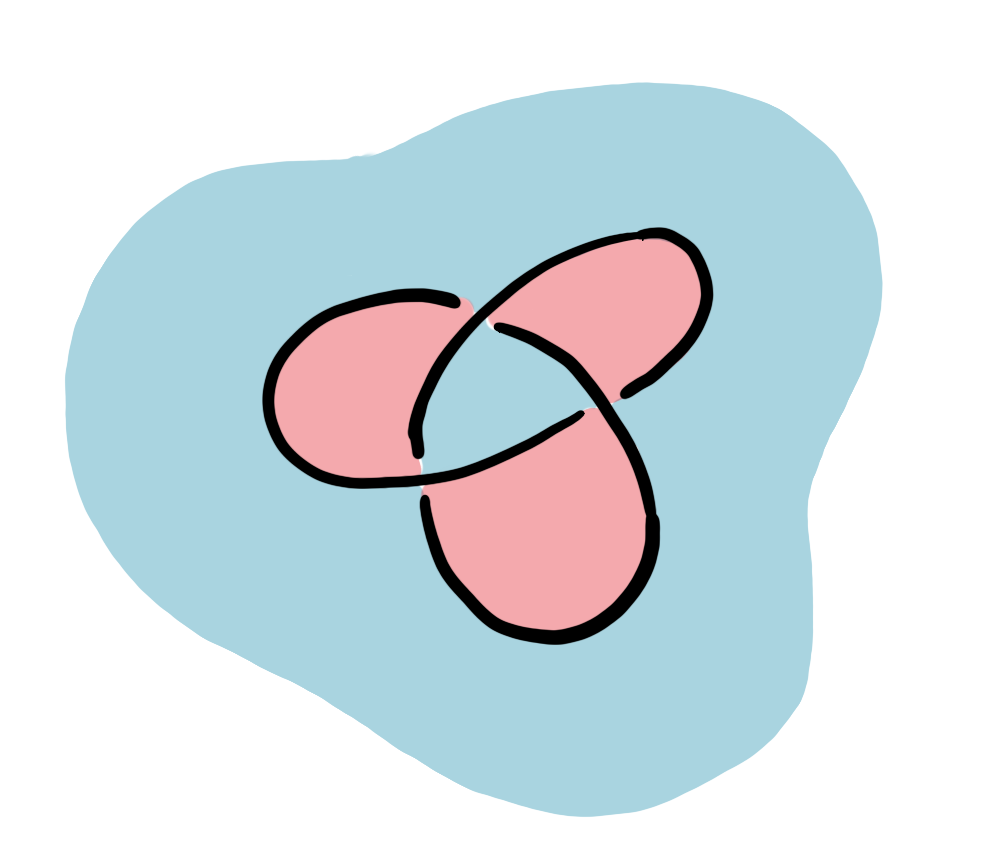
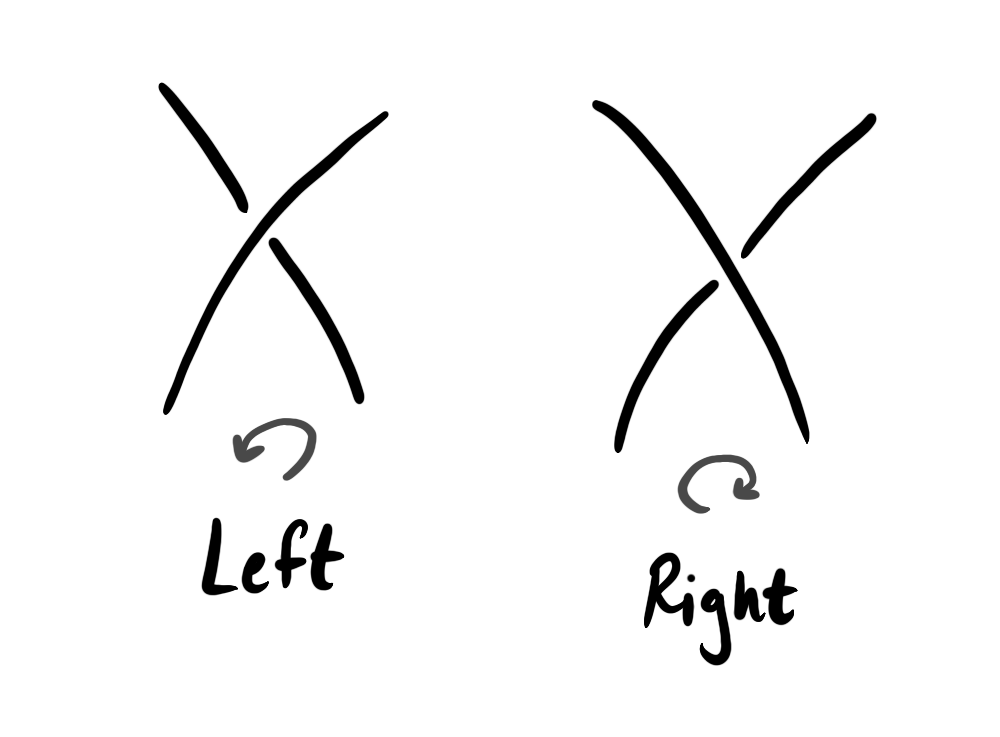
Place a vertex in each red face and connect each pair of vertices once for each crossing between the corresponding faces. Mark these edges \(L\) or \(R\) for a left-hand or right-hand twist. Repeat with the blue faces. Then we have generated two planar graphs which are dual to each other by construction. Each of these graphs encode a Seifert surface. Place a disk at each vertex of the graph and a twisted band with a right or left twist for each edge. We are left with a surface that has the given knot as a boundary.

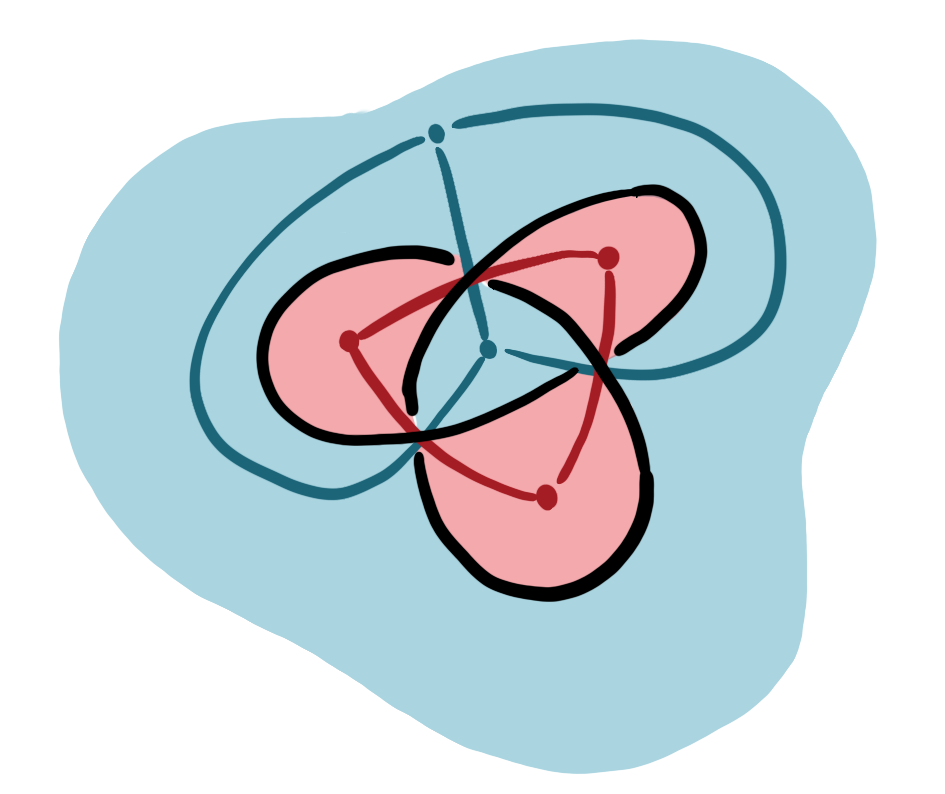
Consider the example above for the trefoil knot. The red graph represents the thrice-twisted Möbius loop; the blue graph provides an alternative Seifert surface. The trefoil is an alternating knot, meaning that all its crossings have the same orientation. Thus, we have omitted the left/right labeling for this example.

Last year I became acquainted with Shiying Dong’s fantastic work in topological crochet. Shiying constructs Seifert surfaces with natural crochet principles by performing a sort of inverse of the process described above. She starts with a graph— some vertices and edges— and imagines each edge as a “ribbon” with thickness. Then she applies a right-hand twist to each edge and reattaches it. If she starts with the blue graph in the figure above (consisting of two vertices with three edges between them), she obtains the orientable Seifert surface for the trefoil.

This is the first crochet project that I learned from Shiying and the first that she teaches in her workshops. You can learn to make one for yourself with my tutorial video or the videos on Shiying’s channel! But without yarn and a crochet hook on hand, we can perform the same process on a graph using pen and paper.

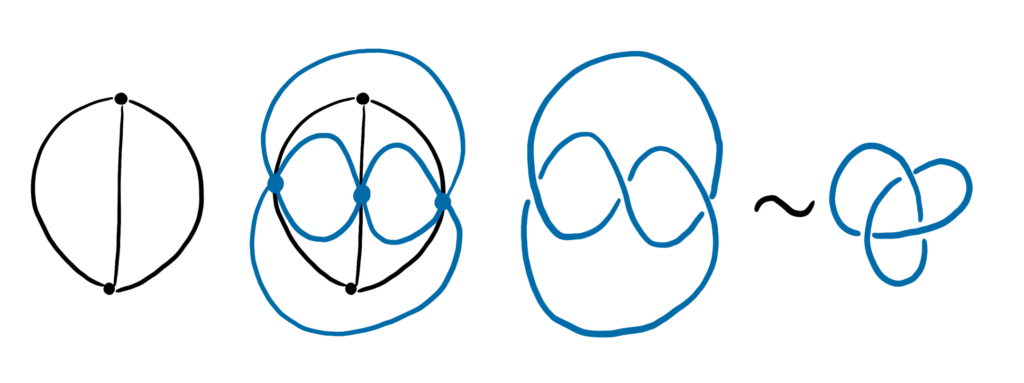
For a general planar graph, the steps are as follows.

1. Draw a planar graph \(G\). It can have double edges and loops, but no edges should cross. The cyclic order of the edges at each vertex is fixed by the embedding into the plane.

2. We will construct a new graph \(H\). Put a vertex of \(H\) on each edge of \(G\) in a new color.

3. A given edge of \(G\) has four “neighboring edges”. If the endpoints of edge \(e\) are vertices \(v\) and \(w\), then the neighboring edges of \(e\) are on its right and left sides in the cyclic order at each vertex \(v\) and \(w\). Some edges may be double counted.

4. Add an edge in \(H\) between two vertices if the corresponding edges in \(G\) are neighbors. Each vertex in \(H\) should have degree 4.

5. At each vertex of \(H\), draw a right-handed crossing.

6. You are left with a knot or a link!

In this process, we have made a universal choice for the handedness of each crossing. This means that all knots and links generated in this way will be alternating. A modification would be to choose the handedness of each crossing individually.

I have really enjoyed trying this on my favorite graphs. Sometimes the resulting knot is surprising and reveals an unexpected connection. In general, it seems difficult to determine which knot or link we obtain—or even the number of link components.

What are the next graphs that you would try? Here, I’ll choose the edge graphs of the Platonic solids. Let’s start with the tetrahedron. Draw four vertices and connect every pair of vertices with an edge. What link do we get when we apply with the process above?

Try for yourself and you will see that we meet another old friend: the Borromean rings. If we continue with the other platonic solids, we obtain two more woven links, one for the cube/octahedron, and one for the icosahedron/dodecahedron. (Recall that dual graphs will give the same link.) These links can be nicely woven by pipe cleaners; thanks to my friend Elliot Kienzle for pointing that out!

Some other great examples to try are the wheel graphs and the edge graphs of prisms. What corresponding graphs and knots can you find? Whether you engage with this question by crocheting surfaces or by doodling graphs, there are many surprises and delights to be found.

Fran Herr is a PhD student in mathematics at the University of Chicago. She studies low dimensional topology and geometric group theory. You can follow her on YouTube and X.

So, which bit of maths has tickled your fancy the most? Vote now!

 Loading ...

The poll closes at 08:00 BST tomorrow. Whoever wins the most votes will get the chance to tell us about more fun maths in the semi-final.

Come back tomorrow for the last quarter-final match, pitting Ayliean against Dave Richeson, or check out the announcement post for your follow-along wall chart!