This is the thirteenth match in our group stage: from Group 1, it’s Lucy Rycroft-Smith up against Alaric Stephen. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Lucy Rycroft-Smith – Counting

Lucy Rycroft-Smith is a researcher and writer at Cambridge Maths (an organisation creating an innovative map of school mathematics 3-19).  She was a maths teacher for ten years across primary, secondary and HE and is the co-editor of Flip the System UK: A Teachers’ Manifesto. She’s @honeypisquared on Twitter.

Have you ever stopped to think about how complicated counting is? By my, er…reckoning, there are at least six separate bits to counting, and they take years to develop. If you’ve ever quizzed a toddler (and may I suggest protective clothing and a manual), you may have noticed all kinds of weird and cool things happening as they assimilate all the mathematical ideas of counting, often in quite a predictable order.  Here’s some of the things you need to be able to do to count even a very small number of things reliably:

Don’t believe me?  Reader, I quizzed that toddler. I got down and dirty with some wonderful young mathematicians to show you just how exciting early counting can be. Here is Evie, an extremely smart mathematician aged three, counting eggs with me.  (No, it was not in French and hence one was not an oeuf).

As you can see, Evie is quite proficient at understanding that one counting word belongs with one object, and is grasping the sophisticated idea that the order of the things you counting doesn’t matter, but the order of the words do.  She hasn’t yet reached the stage, though, where she can start from the count and ‘add on’, trusting that counting a set ends with the final number of the set and vice versa. Look at the way she starts from the beginning of the count again here:

When we teach young mathematicians to count, often we are simply teaching a recital of count-poetry at first, with very little understanding of the abstractness of counting (and no wonder, it’s a REALLY hard thing to grasp). Here is Evie finding it funny as we subvert the count-poem by making counting-noises, which aren’t actually counting, but sound enough like them to be obviously a joke.

And here is Pippa, aged 19 months, showing a high degree of competence and delight at reciting the count-poem but missing the odd one, or forgetting to correspond each noise with an item in the set. Like I said, counting is hard. Please also enjoy the oven timer going off in the video because maths is hungry work and those pizzas need cookin’.

A few years later, young mathematicians will have put together all these skills and started to get at the abstract bit of counting, or the ‘fiveness of five’.  Here’s a ten-year-old mathematician, Millie, explaining some of the elements of counting – you can she is struggling to explain to silly old me what is so obvious to her by this point (there is also an understandable residual degree of contempt because I happen to have birthed this particular mathematician).

As part of an experiment, I asked five high-profile mathematicians to count on their fingers to ten in front of me. (How many can you name? Answers at the end).*Note the slight wariness as they suspect a trap (mathematicians need to stop trying to catch one another out).  Note also the difference in the way that they use their fingers, the order they use them in, the time it takes, and the degree to which they are counting to themselves or counting out towards the audience.  

There is quite a lot of difference, even among this reasonably homogenous group. The way people use their fingers to count has great variation; what is common is that they do use their fingers to count, as a local, convenient, accessible, free and easy-to-use tool that is always (and I’m not even sorry about this) on hand. And yet –and yet, as mathematicians, so often we give the impression that using this tool is infantile or childish, that somehow *imagining* the calculation instead of representing it in front of us is more mathematical or more sophisticated. (We use tools all the time in maths, actually). Finger counting is somehow seen as not polite or what real mathematicians do.  It is scooping your food into your mouth with your hands; it is burping after a good meal; it is staring in the changing room. Why? Using our fingers, not only to count to ourselves, but to signal to others, is a lovely and universal language, beloved of tourists and foreign-language teachers alike. I’ve used my fingers to make not only numbers but also signs and signals to help me teach mathematics in other languages, and I don’t know what I would have done without those dynamic digits. If you have ever struggled with maths, your fingers may have rescued you from the panicky fear of trying to keep track of things, and maybe they still do.  If you are reading this as someone who feels ashamed of using your fingers to do maths: please don’t. You are valid and seen and ok. If it helps you feel better, Professor Anne Watson at Oxford University and I had a lovely discussion of all the many ways she uses her fingers to do maths, including using different hands to keep track of things like tea and coffee orders and also to do times tables. 

But I did just say ‘universal’ language, didn’t I?

Have you seen the film Inglourious Basterds?  

One of the (contentious) plot points involves a wonderful idea: that we use our counting fingers with some kind of accent.  There are, after all, many ways to make three with ten fingers (I count 120…maybe 240 if we are allowed both orientations, palms-forward and palms-backwards). In the film, the spy is found out because he does not, intriguingly, speak ‘finger German’ (I suspect those who use sign language find this idea of a finger dialect not at all odd!).

Look at the differences here among my mathematician friends, when I asked them to hold up a certain number of fingers as a signal – some interesting variations, even in this simple task. Our fingers have other kinds of signatures than just the ones we enact with pens.

I leave you with a nice finger-counting-based joke which also relies on some common frame of finger dialect reference: an ancient Roman walks into a bar, holds up two fingers and shouts ‘five glasses of wine, please!’ 

*Did you get them all?  Susan Okereke, maths teacher and host of podcast Maths Appeal; Bobby Seagull, maths teacher, writer and TV presenter; Andrew Jeffrey, mathemagician, writer and speaker; Ems Lord, director of NRICH at the University of Cambridge; and Mark Dawes, maths teacher and PGCE mentor.

Alaric Stephen – Tournament maths

Alaric Stephen is one of the two hosts of the recreational maths podcast Odds and Evenings. He’s currently teaching Maths and Engineering at Hereford Sixth Form College.

Since we are in a tournament, let’s do a piece of connected mathematics. Let’s say you want to organise an all play all tournament at your local chess club. Every round you pair people up with people that they haven’t played before with the hope that in every round everything slots together with nobody having the sit out and wait unnecessarily. With an even number of players can you always accomplish this?

It doesn’t take long to convince yourself that it’s for 2, 4 or 6 (the first non-trivial case), but as the number of potential fixtures increase it quickly gets hard to calculate manually. If you are looking for a challenge before we dive towards an algorithm, give the 10 case a try.

…

A couple of years ago, my chess club of 12 members was trying to figure out how to arrange just such a blitz tournament one Christmas. We failed badly. Rather than the perfectly packed 11 rounds which are possible, we used 13. The next day at work I presented it as a problem to my maths department and this is what we came up with. Much thanks to my coworker Dr Ali Everett.

I’m going to go through the 6 person tournament with permutation cycle notation. To find our first pairings we are going to use this:

\[ (1,2)(3,4)(5,6) \]

To find who person $n$ plays we scan from left to right finding the next bracket to mention n and reading off the number to the right of it (or, if you are at the end of the bracket, looping back to the start of the bracket, these are cycles). Then using that new number you continue on towards the brackets on the right repeating the process

So, for input 1 we look at the first bracket and get 2. The number 2 isn’t mentioned in the other brackets so we are finished with this iteration and so 1 will play 2. Looking up the other players we get the full matchings for round 1:

• 1-2
• 3-4
• 5-6

On to round 2 our permutation is:

\[ (2,4,5,3,1)(1,2)(3,4)(5,6)(1,3,5,4,2) \]

An input of 1 becomes 2 in the first bracket (remember, these are cycles, so if you reach the end of a bracket you loop back to the beginning), then taking that 2 it becomes 1 again in the bracket (1,2), before finally 1 becomes 3 in the last bracket. Therefore overall input 1 led to output 3. Confused? Here’s the same thing as a picture:

After iterating each input we get the full round 2:

• 1-3
• 2-5
• 4-6

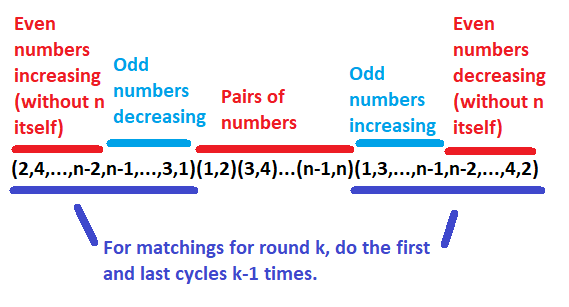
Further rounds are made by adding multiple copies of initial and final brackets onto each end. So round 3 couple be written as:

\[ (2,4,5,3,1)(2,4,5,3,1)(1,2)(3,4)(5,6)(1,3,5,4,2)(1,3,5,4,2) \]

This is easier to think about when you realise that taking the $k$th power of a permutation is the same as taking $k$ steps around it rather than 1. So the above formula you can think of as $(2,4,5,3,1)$ [taking 2 steps] $(1,2)(3,4)(5,6)(1,3,5,4,2)$ [taking 2 steps]

By taking 2 steps, 3 steps and then 4 in those brackets we can get the final rounds of the 6 person tournament:

However all of this was set up so it could be generalised to any number of players. Here’s the case for any even numbered tournament with n players:

The final piece to the problem is dealing with an odd number of people. Unavoidably somebody is going to have to sit out each round. However you can get a maximal solution by using a dummy person to bring the total number of people up to an even number and using the original solution. Whenever someone is due to play the dummy, they have a bye.

So, which bit of maths do you want to win? Vote now!

 Loading ...

The poll closes at 9am BST on the 14th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.

Come back tomorrow for our fourteenth match of the group stages, featuring Vincent Pantaloni and Sameer Shah. Or check out the announcement post for your follow-along wall chart!