
This morning, Twitter was doing its Twitter thing about a maths problem again. Most people were linking to this BBC story, “Crocodile maths question ‘was challenging'”.
Apparently this year’s Scottish New Higher maths exam contained a question which a lot of people found hard. You could remove the word “crocodile” from that headline and obtain a perfectly acceptable statement about a maths exam, but that’s not what people are complaining about.
I had nothing better to do, so I decided to try the question and see if I could make any sense of it. Here’s what happened: (please excuse my terrible handwriting, I was drawing with my finger)
It’s just occurred to me, after making that video, that plotting the function $T(x)$ might be illuminating, so here’s that:
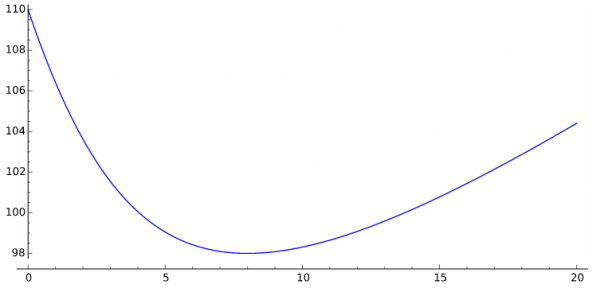
The SQA has put the whole paper online, along with the marking scheme, in case you want to have a look at it yourself. Interestingly, this question has no “commonly observed responses”!
Christian! You missed that T(x) is measured in tenths of a second! So the croc actually takes 9.8 seconds to reach the zebra, which sounds much more reasonable than a minute and a half.
I did! I spotted that first time I read it but completely forgot when I did the video. It’s still silly anyway.
It doesn’t actually matter how far to the right the zebra is, as long as it’s more than 8 metres. The crocodile should always swim 8m along the river (10m diagonally) if it wants to then head along the far bank optimally.
The crocodile behaving optimally is analogous to light coming out of a medium such as glass, where it travels slower than it does in air. The crocodile takes 25% longer to travel each metre in water than on land so the refractive index, n, is 1.25. The critical angle of a medium is asin(1/n). If a ray of light approaches the boundary at that angle from inside the medium, it gets refracted so once it gets out into the air, it travels parallel to the boundary.
If n is 1.25, that angle is asin(1/1.25) = asin(0.8), which is the angle in the 6m, 8m, 10m triangle that marks the crocodile’s route across the river.
Effectively, the crocodile crosses the river at the critical angle and then gets refracted to travel along the bank.
>>It doesn’t actually matter how far to the right the zebra is, as long as it’s more than 8 metres.
This shows up in the fact that the parameter 20 only appears as a constant in T(x) and disappears from the derivative when finding the minimum.
Is there another way to see this? Equivalently, is there a way to find the minimum of T(x) without using calculus?
I think the exam-writers tried to make it “easier” for students by skipping the “construct the function” part of this question, thus leaving the more mechanical bits. They probably didn’t put the speeds and the width of the river in so that students weren’t tempted to try to construct the function themselves and thus “waste time”, but I imagine the effect was just to confuse people. It would probably have been best to put in information about the width of the river and the speeds, even if they were going to do the function for them — students are often aware that exam-writers will do parts of a process for them.
By the way, when I did it I didn’t try to multiply the 16*36, since I was going to divide it by 9 anyway. That gave me:
\[ 9x^2 = 16\times36 \\
x^2 = 16\times4\\
x = 4\times 2 = 8 \]
My issue with this problem is that it tries to embed some math into a “real world” context, but then actual knowledge of that context is in conflict with the math. In this case, there are two conflicts.
First, the crocodile can probably swim faster than it can move on land. They are animals that spend most of their time in the water and are great swimmers. For very short bursts on land, they can also move quickly, but 12m seems too long for one of these short bursts. Also, short land sprints are rare and most footage of crocodiles moving on land shows them going quite slowly. FWIW, there are web references to land speeds of 11kph and swimming speeds of 18 kph or higher (though see below for a caveat on this one).
In any case, given that knowledge, the student’s intuition will be in conflict with the dictated model and should tell them that the crocodile swims the entire distance.
Second, and more importantly, this model is not consistent with the crocodiles’ attack strategy. They don’t make long, wild dashes after prey. Instead, they make use of stealth and patience. The crocodile in this scenario would swim slowly underwater, get as close as possible without detection, and then launch itself out of the water over a short distance. Better yet, the crocodile would already be waiting near the drinking spot, taking advantage of its ability to stay submerged and wait for a very long time.
Because stealth is such a key, it is rare for them to need to swim as fast as possible in the water, hence our lack of clarity about what their maximum swimming speeds are. Contrast with cheetahs, for example, where there is a natural situation in which they need to demonstrate their maximum running speed.
I’ll throw in a third objection: crocodiles and zebra aren’t really part of the “real world” for those sitting the Scottish higher math’s exam. It sits in a strange and uncomfortable third universe that isn’t mathematics and isn’t the actual real world. Perhaps the best name for this odd place is “home of maths word problems.”
Finally, if anyone wants to see a version of the concepts in this problem done well, Dan Meyer’s Taco Cart is the way to go: http://blog.mrmeyer.com/2012/3acts-taco-cart/
I’m considering implementing a +1 function on this site just for that comment. Thanks!
On the one hand, the rest of the two exam papers clearly expects the subject to know some calculus; on the other hand, there is a mild qualitative difference between the present optimization and earlier-requested derivatives (a little chain rule, a radical). So the most interesting question, so far as I can tell, is Whether whoever is sitting for these papers really is supposed to have seen some Calculus, or whether the examiners are fishing for enthusiasts who will have caught it on their own?