Previously, we posted about Katie’s Binary Nail varnish tutorial video, and how you can use glitter (1) and no glitter (0) to encode binary messages in your nail varnish. We also posted an accompanying puzzle, stated as:
Suppose I want to paint my nails on one hand differently every day for a month – so I need to use all 31 combinations involving glitter. Assuming that a nail painted with plain varnish can have glitter added, but a nail with glitter needs to be nail-varnish-removed before it can become a plain nail again, what order do I apply the different combinations so that you minimise the amount of nail varnish remover I’ll need to use?
Here’s our take on the solution.
First of all, there’s a slightly subtle point to note – there’s a similar question you can ask, to which there is an easy and well-known answer. If instead we were asking how to minimise the number of times I need to change a nail, either from glitter to no glitter or back again, that’s the same as asking how to minimise the number of flips from 0 to 1 or from 1 to 0. The answer to this is to use a Gray code.
A Gray code – sometimes known as reflected binary code, and named after its creator Frank Gray – is an ordering of numbers such that each successive pair of numbers differ in only one bit (binary digit). Patented in 1947, it was originally designed to minimise errors in mechanical switching systems – if more than one switch has to flip to change between two numbers, they might not flip at exactly the same time, so the output might temporarily read or print out a number unintentionally. In the conventional order, binary numbers sometimes involve flipping multiple bits – such as going from 3 (011) to 4 (100), in which all three bits flip; the Gray code is an alternative ordering that can be worked out for any set of numbers $0 \ldots 2^n-1$ to ensure each switch is only one digit – for example, the numbers 0 to 7 can be written in the following order with only single bit-flips:
| 0 | 000 |
| 1 | 001 |
| 3 | 011 |
| 2 | 010 |
| 6 | 110 |
| 7 | 111 |
| 5 | 101 |
| 4 | 101 |
In fact, the binary combinations above are referred to as the Gray code for the numbers 0 to 7, in that order, so Gray code for 2 is 011 (even though that’s 3 in binary).
A Gray code for an $n$-bit sequence can be constructed from the $(n-1)$-bit Gray code, in quite a pleasing way. To go from 2-bit to 3-bit, take the sequence for 2-bit:
00, 01, 11, 10
Add a reflected version of this same string to the end:
00, 01, 11, 10, 10, 11, 01, 00
Then prefix the first half with 0s and the second half with 1s:
000, 001, 011, 010, 110, 111, 101, 100
This process can be repeated to generate the 4-bit sequence, and so on.
Since its creation, the Gray Code has been used in error correction and digital logic, and it can also be used to solve the Towers of Hanoi puzzle. As far as I know, the present work is the first application to personal grooming.
So, if I were to use the Gray Code ordering for my nails, I’d get the following sequence:
| Order | Gray Code | Decimal equivalent | Order | Gray Code | Decimal equivalent | Order | Gray Code | Decimal equivalent |
|---|---|---|---|---|---|---|---|---|
| 0 | 00000 |
0 | 11 | 01110 |
14 | 22 | 11101 |
29 |
| 1 | 00001 |
1 | 12 | 01010 |
10 | 23 | 11100 |
28 |
| 2 | 00011 |
3 | 13 | 01011 |
11 | 24 | 10100 |
20 |
| 3 | 00010 |
2 | 14 | 01001 |
9 | 25 | 10101 |
21 |
| 4 | 00110 |
6 | 15 | 01000 |
8 | 26 | 10111 |
23 |
| 5 | 00111 |
7 | 16 | 11000 |
24 | 27 | 10110 |
22 |
| 6 | 00101 |
5 | 17 | 11001 |
25 | 28 | 10010 |
18 |
| 7 | 00100 |
4 | 18 | 11011 |
27 | 29 | 10011 |
19 |
| 8 | 01100 |
12 | 19 | 11010 |
26 | 30 | 10001 |
17 |
| 9 | 01101 |
13 | 20 | 11110 |
30 | 31 | 10000 |
16 |
| 10 | 01111 |
15 | 21 | 11111 |
31 |
Each time I change from one nail to the next, I’m changing exactly one nail – either adding glitter, or removing it, and this is undeniably the most efficient way. But the question we asked in our puzzle was slightly different – since it’s much more effort to remove nail glitter than to add it, can we minimise the number of glitter removals, i.e. changes from 1 to 0?
If you’d like to try and work it out for yourself, go and do that now.
Minimising Glitter Removals
The first question you might ask is, is Gray Code the answer here too? In the list given above, there are 15 instances of switching from a 1 to a 0. But it can be done in fewer!
Our first breakthrough here was to find a solution more efficient than the Gray Code ordering, and we did find an ordering which takes 14 removes (for the record, it was 0, 2, 3, 1, 5, 4, 6, 7, 11, 10, 8, 9, 13, 12, 14, 15, 23, 22, 20, 21, 17, 19, 18, 16, 24, 26, 27, 25, 29, 28, 30, 31). But can we do any better?
It’s actually possible to prove that the lower bound on this — the fewest removals any valid solution can have — is 13. Let’s assume that each move consists of removing or adding exactly one nail’s glitter, and note that there are 31 ‘steps’ to achieve all 32 positions. If you start with no nails glittered and finish with all five glittered, the difference between the number of moves adding and removing glitter must be at most five, and therefore the minimal solution in terms of removals must have 18 adds and 13 removes making up the 31 steps.
All we need now is to actually find a way of doing it with only 13 removals. Ooh, here’s one:
| Order | Binary | Decimal Equivalent | Order | Binary | Decimal Equivalent | Order | Binary | Decimal Equivalent |
|---|---|---|---|---|---|---|---|---|
| 0 | 00000 |
0 | 11 | 01000 |
8 | 22 | 10010 |
20 |
| 1 | 00001 |
1 | 12 | 01010 |
10 | 23 | 10011 |
22 |
| 2 | 00011 |
3 | 13 | 01011 |
11 | 24 | 10111 |
23 |
| 3 | 00010 |
2 | 14 | 01111 |
15 | 25 | 10101 |
21 |
| 4 | 00110 |
6 | 15 | 01110 |
14 | 26 | 10001 |
17 |
| 5 | 00111 |
7 | 16 | 11110 |
30 | 27 | 10011 |
19 |
| 6 | 00101 |
5 | 17 | 11100 |
28 | 28 | 11011 |
27 |
| 7 | 00100 |
4 | 18 | 11000 |
24 | 29 | 11001 |
25 |
| 8 | 01100 |
12 | 19 | 11010 |
26 | 30 | 11101 |
29 |
| 9 | 01101 |
13 | 20 | 10010 |
18 | 31 | 11111 |
31 |
| 10 | 01001 |
9 | 21 | 10000 |
16 |
One obvious way to find the most efficient solution is to crunch it all through a computer: generate all the possible orderings, and count how many removals you need in each case. Of course, this would take a huge amount of computer time – the number of possible orderings is 32!, which is 263130836933693530167218012160000000, and as you can see below in the results of a simulation of 126,000 randomly-chosen orderings in R, only a tiny proportion achieve fewer than thirty removals, let alone thirteen.
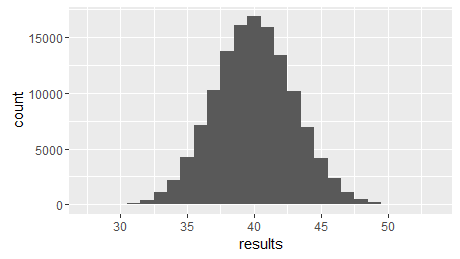 So instead of relying on luck, we used a bit of maths thinking. The standard Gray Code that will solve you the Tower of Hanoi looks like this
So instead of relying on luck, we used a bit of maths thinking. The standard Gray Code that will solve you the Tower of Hanoi looks like this
\[1213121412131215121312141213121\]
where each digit represents the nail you change at each step (or which disk you move to a new peg). The problem with the standard solution for our purposes is that, starting with five unglittered nails, it doesn’t end with all fingers glittered — it ends with only digit 5 glittered. Fortunately, it’s easy to modify the sequence to change this.
Consider the simpler case of a three-fingered mathematician. They can imagine their nail-painting journey as a trip round the edges of a cube visiting every corner, with forwards and backwards movemement in each of the three dimensions correpsonding to glittering and unglittering each of the three nails. The picture below shows how the standard Gray Code solution can be modified to create a minimal-removals, no-glitter to all-glitter, solution, which on the cube corresponds to a path starting and ending at opposite corners.
Switching 1s for 2s and vice versa in the second 121 subection has done the trick here, but for the five-nails case it’s a bit more complex. It’s hard to visualise a trip round a five-dimensional hypercube, so let’s return to the digit sequence. Starting and ending at opposite corners happens if and only if each digit appears in the sequence an odd number of times (an even number of changes puts you back where you started). In the longer five-digit sequence we can still switch 1s and 2s in a 121 subsequence, but we can also switch around the 1s, 2s and 3s in a larger 1213121 subsequence, or even the 1s, 2s, 3s and 4s in one of the two big 121312141213121 chunks. A brief bit of faffing around before too long delivered this sequence:
\[1213121413121315232423212324232\]
where we’ve switched 2s with 3s in the second 1213121 chunk, and changed the 1s to 2s, 2s to 3s, 3s to 4s and the 4 to a 1 in the second 121312141213121 chunk. This sequence of digit-changes contains each digit an odd number of times, and gives the full sequence of nails tabulated above.
Having found this one solution, any equivalent solution made by permuting the five columns of binary digits will also only involve 13 removals; plus there are other tweaks you can make to the ordering using the method above. So, this solution generates hundreds of potential other 13-remove solutions. We’ve not ascertained whether all solutions that take exactly 13 can be found in this way from this one, or whether there are multiple classes out there, but this is pretty satisfying.
As always, CL-P has done his usual trick and built an interactive version of this problem, so you can play around with it for yourself and see if you can find a different solution with 13 removals:

This is a intriguing problem and you provide an interesting and really educational solution. In the interests of pedantry, we could point out that in the sample solution the binary for step 22 and step 23 does not match the decimal value.