This post is part of a series of posts by guest author Joshua Holden.

I ended Part I with the observation that the Monster group was connected with the symmetries of a group sitting in 196883-dimensional space, whereas the number 196884 appeared as part of a function used in number theory, the study of the properties of whole numbers.  In particular, a mathematician named John McKay noticed the number as one of the coefficients of a modular form.  Modular forms also exhibit a type of symmetry, namely if F is a modular form then there is some number k for which

$$F\left(\frac{az+b}{cz+d}\right)= \frac{1}{(cz+d)^k} F(z)$$

for every set of whole numbers a, b, c, and d such that ad–bc=1.

Modular forms, elliptic curves, and Fermat’s Last Theorem

In 1954, Martin Eichler was studying modular forms and observing patterns in their coefficients.  For example, take the modular form

$$F(e^{2 π i z}) = e^{2 π i z} \prod_{n=1}^\infty\left[(1- e^{2 π i z n})^2 (1- e^{2 π i z 11 n})^2\right]$$

The coefficients of this modular form seem to be related to the number of whole number solutions of the equation

y² = x³ – 4 x² + 16

This equation is an example of what is known as an elliptic curve, which is a curve given by an equation of the form

y² = x³ + ax² + bx + c

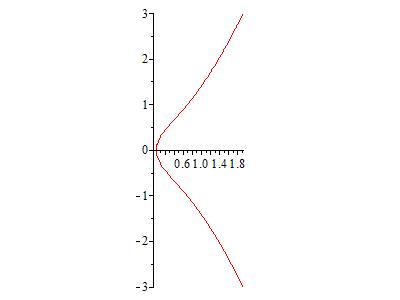
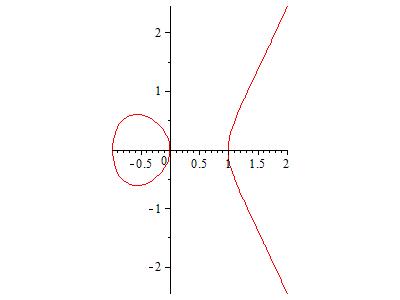
Elliptic curves have one line of symmetry, two open ends, and either one or two pieces, as shown in Figures 1 and 2. They are called elliptic curves because the equations came up in the seventeenth century when mathematicians started studying the arc length of an ellipse.  These curves are considered the next most complicated type of curve after lines and conic sections, both of which have been understood pretty well since at least the ancient Greeks.   They are useful for a lot of things, including cryptography, as I describe in Section 8.3 of The Mathematics of Secrets.

In the late 1950’s it was conjectured that every elliptic curve was related to a modular form in the way that the example above is.  Proving this “Modularity Conjecture” took on more urgency in the 1980’s, when it was shown that showing the conjecture was true would also prove Fermat’s famous Last Theorem.  In 1995 Andrew Wiles, with help from Richard Taylor, proved enough of the Modularity Conjecture to show that Fermat’s Last Theorem was true, and the rest of the Modularity Conjecture was filled in over the next six years by Taylor and several of his associates.

Modular forms, the Monster, and Moonshine

Modular forms are also related to other shapes besides elliptic curves, and in the 1970’s John McKay and John Thompson became convinced that the modular form

J(z) = e ^{-2 π i z} + 196884 e ^{2 π i z} + 21493760 e ^{4 π i z}  + 864299970 e ^{6 π i z}  + …

was related to the Monster.  Not only was 196884 equal to 196883 + 1, but 21493760 was equal to 21296876 + 196883 + 1, and 21296876 was also a number that came up in the study of the Monster.  Thompson suggested that there should be a natural way of associating the Monster with an infinite-dimensional shape, where the infinite-dimensional shape broke up into finite-dimensional pieces with each piece having a dimension corresponding to one of the coefficients of J(z).   This shape was (later) given the name V♮, using the natural sign from musical notation in a typically mathematical pun. 

John Conway and Simon Norton formulated some guesses about the exact connection between the Monster and V♮, and gave them the name “Moonshine Conjectures” to reflect their speculative and rather unlikely-seeming nature. A plausible candidate for V♮ was constructed in the 1980’s and Richard Borcherds proved in 1992 that the candidate satisfied the Moonshine Conjectures.  This work was specifically cited when Borcherds was awarded the Fields medal in 1998.

The construction of V♮ turned out also to have a close connection with mathematical physics.  The reconciliation of gravity with quantum mechanics is one of the central problems of modern physics, and most physicists think that string theory is likely to be key to this resolution.  In string theory, the objects we traditionally think of as particles, like electrons and quarks, are really tiny strings curled up in many dimensions, most of which are two small for us to see.  An important question about this theory is exactly what shape these dimensions curl into.  One possibility is a 24-dimensional shape where the possible configurations of strings in the shape are described by V♮.  However, there are many other possible shapes and it is not known how to determine which one really corresponds to our world.

More Moonshine?

Since Borcherds’ proof, many variations of the original “Monstrous Moonshine” have been explored.  The other members of the Happy Family can be shown to have Moonshine relationships similar to those of the Monster.  “Modular Moonshine” says that certain elements of the Monster group should have their own infinite dimensional shapes, related to but not the same as V♮.  “Mathieu Moonshine” shows that one particular group in the Happy Family has its own shape, entirely different from V♮, and “Umbral Moonshine” extends this to 23 other related groups which are not simple groups.  But the Pariah groups remained outsiders, rejected by both the Happy Family and by Moonshine — until September 2017.