This is a guest post by mathematician and maths communicator Ben Sparks.
Roger Apéry: 14th November 1916 – 18th December 1994
100 years ago (on 14th November) was born a Frenchman called Roger Apéry. He died in 1994, is buried in Paris, and upon his tombstone is the cryptic inscription:
\[ 1 + \frac{1}{8} + \frac{1}{27} +\frac{1}{64} + \cdots \neq \frac{p}{q} \]
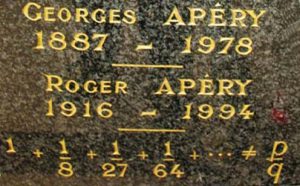
Apéry’s gravestone – Image from St. Andrews MacTutor Archive

Roger Apéry – Image from St. Andrews MacTutor Archive
The centenary of Roger Apéry’s birth is an appropriate time to unpack something of this mathematical story.