In what flipping dimension is a square peg in a round hole just as good as a round peg in a square hole?

Let’s start at the beginning.

My Plus magazine puzzle from March asks “Which gives a tighter fit: a square peg in a round hole or a round peg in a square hole?” By “tighter” we mean that a higher proportion of the hole is occupied by the peg.

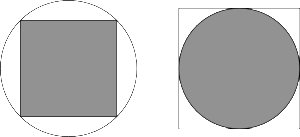
Note that everything is scalable when considering fit: think of shrinking or expanding the images above with a photocopier; it’s only the ratios of areas that are important, not the specific measurements.

This question has been asked and answered many times before, and in generalised form too (more on that below).

One could also ask which is a better fit on the internet, by comparing Google hits for “round peg in a square hole” versus “square peg in a round hole”. The latter has been gaining popularity for over a century, at least since Edward Bulwer Lytton wrote

You … insist upon forcing a square peg into a round hole, because in a round hole you, being a round peg, feel tight and comfortable. Now I call that irrational.

Have those who use this phrase considered the alternative above, and done the maths? Probably not.

Ponder this related puzzle.

What portion of the large square does the small square cover?

The answer to that one is “one half” — just imagine that the inner square is rotated ${45}^{\circ }$ and it becomes pretty clear, without any computation at all. This observation allows us to answer our question too.

Assume that the larger square in the triple nested image above has width $2$, and hence area $4$. Upon reflection—and rotation, as just suggested—the smaller inside square must have area $2$ (an application of Pythagoras also confirms this). The circle has area $\pi$ of course.

So the square peg in a round hole fit is $\frac{2}{\pi }$, and the round peg in a square hole fit is $\frac{\pi }{4}$.

Since $\pi >3$ it follows that ${\pi }^2>8$, and hence $\pi >\frac{8}{\pi }$. Dividing by $4$ yields $\frac{\pi }{4}>\frac{2}{\pi }$.

Hence, a round peg in a square hole is a better fit than a square peg in a round hole!

As decimal approximations, we are comparing $0.7854$ with $0.6366$: a round peg fills up about 78.54% of a square hole, whereas a square peg only fills up about 63.66% of a round hole.

Maybe that’s why we sometimes see round tins in rectangular boxes, but square bottles such as those pictured on the right are rarely packed in cylindrical boxes, since the latter is a less economical use of space.

If we’re going to move up a little in dimension, from $2$, let’s go all the way to $3$, and ask:

Is a sphere in a cube also a better fit than a cube in a sphere? Can you do the appropriate computations in this case? Does it help to consider the 3D analogue of the nested image above, this time of a cube in a sphere in a cube, and then rotate the inner cube?

It’s fun to envision a sphere starting inside a cube and then expanding until it perfectly encloses the cube.

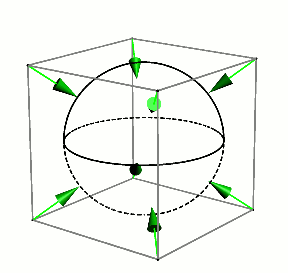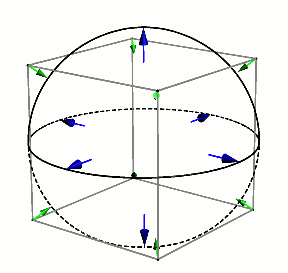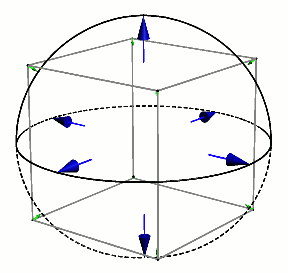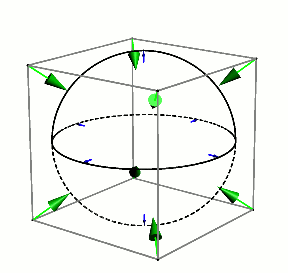
It turns out that we are comparing $\frac{\pi }{6}$ (52.36% filled) and $\frac{2}{\pi \sqrt{3}}$ ( 36.76% filled)

What about in dimension $4$? That’s a little harder for most of us to visualise, unless you have the 4D instincts of somebody like geometer Tom Banchoff! Is a $4$-ball a better fit in a $4$-cube than a $4$-cube in a $4$-ball?

Here, it turns out that we are comparing $\frac{{\pi }^2}{32}$ (30.84% filled) and $\frac{2}{{\pi }^2}$ ( 20.26% filled)

Notice that we are getting poorer fits in both cases as the dimension goes up. It gets worse (before it gets weird).

How is your sixth sense? In 6D we are comparing $\frac{{\pi }^3}{384}$ (8.07% filled) and $\frac{16}{9{\pi }^3}$ ($5.73% filled)

In 8D it drops to $\frac{{\pi }^4}{6144}$ (1.59%) versus $\frac{3}{2{\pi }^4}$ (1.54%), and by 10D, it’s $\frac{{\pi }^5}{122880}$ (0.025%) versus $\frac{768}{625{\pi }^5}$ (0.04%).

The pattern of poorer performance persists. But wait, the fit facts have flipped: apparently, when $n=10$, an $n$-sphere in an $n$-cube is a worse fit than an $n$-cube in an $n$-sphere!

Actually, the flip took place before the tenth dimension.

David Singmaster (now a London resident) examined this in detail half a century ago, computing the appropriate ratios of hypervolumes, and published his results in a November 1964 paper called “On Round Pegs in Square Holes and Square Pegs in Round Holes” in Mathematics Magazine, 37, 335-339, which is also available in the recent MAA/Cambridge book “Harmony of the World — 75 Years of Mathematics Magazine“.

His conclusion was that an $n$-ball in an $n$-cube is indeed a better fit than an $n$-cube in an $n$-ball, for $n=2,3,4,5,6,7$ and $8$, but that the situation is reversed from dimension $9$ onwards.

There is a sense in which things flip as we cross a mysterious dimension around $8.13794$ (see OEIS sequence A127454).

As discussed by Singmaster and summarised in the MathWorld article on the question, the formulae to be compared (in a particular dimension) involve factorials, and hence can be generalised to non-whole numbers using the Gamma function. Those generalised hypervolumes agree for the specific dimension number between $8$ and $9$ mentioned above.

So the answer to the question “In what flipping dimension is a square peg in a round hole just as good as a round peg in a square hole?” is, “In dimension $8.13794$, more or less!” ((Another flipping question—which is of peripheral interest when coding with playing cards—namely “for what number n between $3$ and $4$ does $n!$ first pass out $2^n$ ?” was only noted at the On-Line Encyclopedia of Integer Sequences quite recently, by this author.))

As for the continually shrinking numbers representing quality of fit, an anonymous comment at the Plus magazine puzzle site pointedly remarks, “Roughly speaking as you increase the number of dimensions, more and more of the volume of the hypercube is out near its corners – high dimension cubes are qualitatively more like hedgehogs than building blocks!”

Wolverhampton native (and unrepentant Hammers fan) Andew Worsey raises another interesting question in the comments following the Plus magazine puzzle:

“Is the same true for any regular $m$-gon, as opposed to the square, when you look at the inscribed and circumscribed circles, and what is the limiting behaviour?

Why not start with $m=3$, that is to say the case of equilateral triangles and circles! Then try pentagons, hexagons, and so on. For any regular $m$-gon, the question is readily settled using trigonometry.

How about generalising that too, say to regular polyhedra and spheres in the third dimension? Try it for the four platonic solids other than the cube. For instance, does a sphere fit better in a dodecahedron than the other way around?

Moving up to higher dimensions, you need to consider the analogues of the Platonic solids, namely polytopes. In the fourth dimension, there are five non-hypercube polytopes to consider, but from dimension five on, there are only two possible non-hypercube polytopes.

Incidentally, it’s not just $n$-balls and $n$-cubes that surprise (by reversing roles) starting in dimension $9$. In the “Spheres and Hyperspheres” chapter of Martin Gardner’s Mathematical Circus (MAA, 1981) there’s a discussion of several strange phenomena which occur for the first time in dimension 9, including the one above and also a sphere packing paradox of Leo Moser’s. (Some of this is reproduced in the Gardner compendium “The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems“.)

One can of course become beautifully befuddled in lower and much more familiar dimensions. We leave you with the following problem, which Gardner observed is equivalent to a celestial conundrum over which Isaac Newton and Oxford astronomer David Gregory argued circa 1694, and which was not definitively settled for another 180 years:

Can 13 paper circles, each covering a 60-degree arc of a great circle on a sphere, be pasted on that sphere without overlapping?