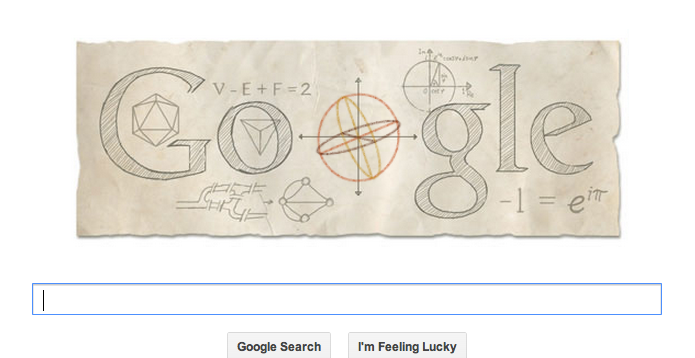
Today is Euler’s $-306 \times e^{i \pi}$^th birthday, and Google have chosen to celebrate (despite ignoring several other prominent mathematical birthdays, including Erdős’s centenary – see the @MathsHistory twitter feed for a full list) by creating a Google doodle on their homepage.

For anyone who isn’t aware, this is when Google changes the image above the search box on the homepage at Google.com, so it still says ‘Google’ but using an appropriate image, which sometimes has built-in interactive elements. I thought it was worth pointing out some of the fantastic maths they’ve included in today’s doodle.

In celebration of the Swiss mathmo’s achievements, the Google doodle today includes:

• The formula for the Euler characteristic, $V – E + F = 2$, which relates the number of vertices, edges and faces of a spherical polyhedron. The doodle also features some polyhedra (icosahedron and tetrahedron). The formula also applies to a diagram of vertices, edges and faces drawn on a flat plane, or on a sphere – and a similar one can be used for on other surfaces, by subtracting 2 from the right hand side for each hole in the object (so on a donut, $V – E + F = 0$).
• The famous ‘Seven bridges of Königsberg‘ problem, drawn as both the layout of bridges and a graph. Euler pioneered graph theory; an Eulerian graph is one which can be fully traversed starting from any point (equivalently, one where each node has an even number of arcs coming into it). Since the ‘bridges of Königsberg’ graph has an odd number of arcs coming into every node, it can’t be traversed from any start point – although if a graph has all even nodes apart from two, it’s called semi-Eulerian, and can be traversed only if you start at one odd node and end at the other.
• Euler’s identity, $-1 = e^{i \pi}$. This is often described as one of the most beautiful equations in mathematics – if you rewrite it as $e^{i \pi} + 1 = 0$, you have a relation involving five amazing constants (the additive and multiplicative identities, $0$ and $1$, plus the exponential constant $e$, circle constant $\pi$ and the imaginary number $i$) as well as all the major mathematical operations – addition, multiplication (between $i$ and $\pi$) and exponentiation. This relationship expresses nicely the connection between trigonometry and the exponential function, and it’s boss as heck.
• There’s also a geometrical interpretation of Euler’s formula, which shows how as the angle changes, the real and imaginary parts of the points on a circle in the complex plane change according to trigonometric functions.
• At the centre of the Google doodle is a three-dimensional representation of a sphere, which you can drag around and it will rotate in all three axes. Within the sphere you can see three orthogonal sections, creating a cross in each plane. Euler introduced the idea of Euler angles, to describe the orientation of a rigid body using an angle of rotation around each of the three Cartesian axes. This way of describing angles is widely used, from Euler’s time right through to modern day technology such as accelerometers – these are used in mobile computing devices and controllers to measure the position and motion in space of the object, which can be used to control the device (think Wiimotes, and tilty marble games on your phone, and then think of Euler and be grateful.)

Props to Google for popularising Euler’s amazing work, and for making such a lovely doodle! Also, Google, if you’re looking to employ someone to research and create amazing mathematical doodles like this in future, I’m totally available. Although I imagine there are enough Google employees interested enough in maths that they don’t have a problem there.