The Online Encyclopedia of Integer Sequences contains over 200,000 sequences. It contains classics, curios, thousands of derivatives entered purely for completeness’s sake, short sequences whose completion would be a huge mathematical achievement, and some entries which are just downright silly.
For a lark, David and I have decided to review some of the Encyclopedia’s sequences. We’re rating sequences on four axes: Novelty, Aesthetics, Explicability and Completeness.
Following last week’s palaver, we’re going to do our best to be serious this time. Game faces on.
A052486
Achilles numbers – powerful but imperfect: writing n=product(p_i^e_i) then none of the e_i=1 (i.e. powerful(1)) but the highest common factor of the e_i>1 is 1 (so not perfect powers).72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, 1125, 1152, 1323, 1352, 1372, 1568, 1800, 1944, 2000, 2312, 2592, 2700, 2888, 3087, 3200, 3267, 3456, 3528, 3872, 3888, 4000, 4232, 4500, 4563, 4608, 5000, 5292, 5324, 5400, 5408, 5488, ...
Explicability
Christian: “Powerful but imperfect”… a bit like you, then?
David: ?!
Christian: Actually, we can draw a Venn diagram. Hang on…
…
Christian: Oh no I got it wrong. Continue hanging on…
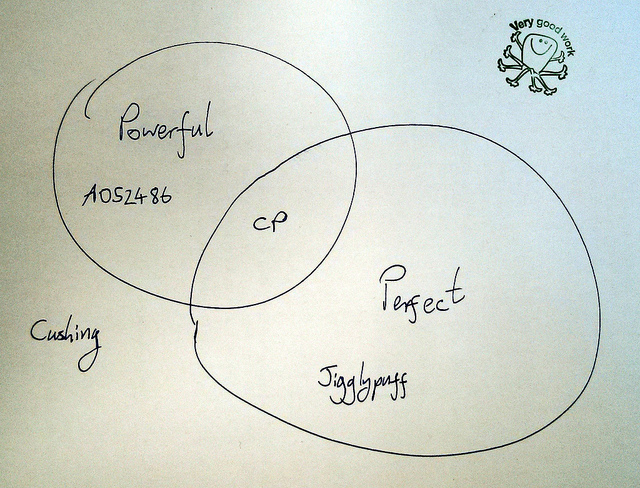
Christian: Good work on the stamp.
David: Anyway, back to the explanation. A number is POWERFUL if all the powers in its prime decomposition are bigger than 1 – so if a prime divides it, its square does as well.
Christian: Ah, we are punning. Very droll.
David: I didn’t make a pun!
Christian: Not you, whoever invented powerful numbers.
David: You mean Achilles?
Christian: Have we explained it? Can we give a score?
David: Hold your horses. An Achilles number is a POWERFUL number which is not a perfect power.
Christian: OK! Four out of five. Yes?
Novelty
Christian: I don’t like this category any more.
David: Why?
Christian: All the interesting sequences were thought up ages ago. Actually, maybe this one wasn’t. I might have been misled by Achilles. You could call my tendency to jump to conclusions my… Achilles heel!

Christian: It was added to the OEIS in 2000 with no references. So it’s fairly new.
David: I was going to say it should lose 1 for being a subsequence of another sequence, but every sequence is a subsequence of another sequence.
Christian: I put it to you, Cushing, that it’s the very act of taking a subsequence that is novel. Anyway, what fresh new ideas has this one got going for it?
David: I don’t care any more. Three.
Christian: No, it’s a new idea to me. More: four.
David: We found it when I thought I had a new sequence. So it’s not that novel.
Aesthetics
David: All these numbers are sexy. They’re so full and yet so empty.
Christian: Like Quavers?
David: EXACTLY like Quavers. I am worried about all the zeroes.
Christian: I don’t think they turn up particularly often. You need to have both 2 and 5 as factors, which asymptotically almost no Achilles numbers do.
(David points out all the zeroes in the first 80 entries)
Christian: Have faith! Once we get to the bigger primes there will be fewer zeroes. Because of combinatorics, you’ll get lots of fives and twos at the start.
David: What about 5,000,000,000? That’s a lot of zeroes. And it’s Achilles.
Christian: I’m not denying that there are zeroes, I’m just saying there aren’t too many.
David: You pick the score. I’m sad now I’ve run out of chocolate raisins.
Christian: Actually, we still need to discuss this. I want to give it a high score, but it hasn’t moved me to tears of joy.
David: 72 is such a beautiful number! I think all the numbers here are beautiful by themselves. But you can have too much beauty. Three out of five.
Christian: We’ll stick with four.
Completeness
David: Is there a way to generate them all?
Christian: Like a generating function? I’m sure there is.
David: To the OEIS!
<batman noises>
Christian: The OEIS doesn’t have one. Why not? We just want vectors in… what do you call the space with infinitely many dimensions?
David:
Christian: Yeah. There’s a bijection with the reals.
David: So there are uncountably many Achilles numbers. Now this is a palaver. Let’s quickly move on and give it a 4.
Christian: Let’s play it safe. Five.
Total score
David: STOP THE PRESSES! We only want vectors from
Christian: Can you write down a generating function yet?
David: I’ll do it later.
Christian: Well, pending that, we’ll add up a provisional score.
Christian: Something seems wrong. Oh well. We’ve got bigger troubles at the moment.
David: We should review it again next week but give it a Novelty score of 1 because we’ve seen it before. And I’ll work on a generating function.
Will our intrepid heroes find a generating function? Will they ever review a sequence sensibly? Will David get credited next time this series appears in the Carnival of Maths? Find out next week, same Bat-time, same Bat-place!
There’s an
Goodness, that’s ugly…
Good work! Using the Möbius function to pick out squarefree numbers feels a little bit like cheating, but it’s better than what we came up with.
Not sure if you have seen it before (I’m surprised I haven’t) but there is an (unofficial) oeis movie http://www.youtube.com/watch?v=LCWglXljevY