You're reading: Blackboard Bold, Features

How to solve a Rubik’s Cube in one easy step

By . Posted in Blackboard Bold, Features

Note: If you’re looking for instructions on solving Rubik’s cube from any position, there’s a good page at Think Maths.

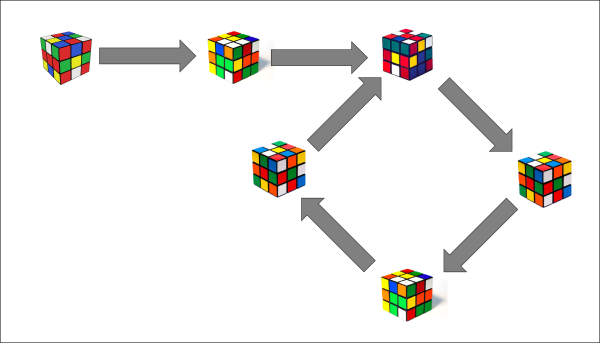
One day some years ago I was sat at my desk idly toying with the office Rubik’s cube. Not attempting to solve it, I was just doing the same moves again and again. Particularly I was rotating one face a quarter-turn then rotating the whole cube by an orthogonal quarter-turn like this:


Having started with a solved cube, I knew eventually if I kept doing the same thing the cube would solve itself. But this didn’t seem to be happening – and I’d been doing this for some time by now. This seemed worthy of proper investigation.

The first thing to sort out is, how did I know the cube would eventually solve itself if I kept doing this same thing over again? Well, a pretty obvious fact about a Rubik’s cube its that it’s non-random. If two cubes are in the same state and you do the same moves on both, they’ll both end up in the same state. The initial state and the moves together determine the end state. So as you repeat the same sequence of moves, the cube tracks through different states in a predetermined way. There’s a finite number of states the cube can be in (rather more than the 3 billion that the product’s marketing originally claimed but still a finite number) so eventually it will hit a state it’s been in before. From then the cube will be stuck Groundhog-Day-style in its previous pattern; the same states and the same moves producing the same results.

But this doesn’t prove that the cube will return to its initial solved state. Why could the following not happen?

Rubik's cube configuration diagram

Do not let this diagram unsettle you; it will shortly turn out to be impossible.

If the cube doesn’t go back to a solved state, it must do this, landing on some previously seen non-solved position and from there entering a loop. But look at the first cube in the loop. It’s reached from two different states. Another pretty obvious fact about the Rubik’s cube is that any move, or sequence of moves, can be reversed. If I can twist a face then spin the cube, I can just as well spin the cube the other way then twist it backwards. Doing a move then doing its inverse will have no net effect on its state. So suppose the cube is in one of the two states feeding in to the loop, and I do my twist-and-spin move combo then its spin-and-twist inverse. In both cases we must end up with the cube as it started. But both start by twist-and-spinning the cube into the first state of the loop. But then we have the curious situation where both cases involve having a cube in this state, both have the spin-and-twist ‘undo’ moves applied, but both end up in different states. We know this doesn’t happen. The only way to reconcile this paradox is if the loop goes right back to the initial solved state, so that the two-into-one problem does not arise.

Compare this state of affairs to Conway’s Life, the ‘zero-player game’ wherein a grid of black and white squares changes over time according to a simple rule that can give rise to almost endless variety. Given an initial state for Life and its one repeated ‘move’, what can (and very often does) happen is that the game gets locked into an infinitely-repeating pattern that does not begin with a repetition of the initial game state. That’s because the move in Life is not invertible; you can reach the same position from two different previous states, so the ‘lasso’ pattern above does occur.

Now we know I will eventually ‘solve’ the Rubik’s cube with my twist-spin moves, but the question remains when? Since my office was in the maths department at Manchester University, we decided to work it out, and do it the only way we knew how: with stickers and computers.

Stickered Rubik's Cube

Stickered-up Rubik’s Cube, pictured with a Manchester University maths department pencil

With the little ‘facelets’ of the cube numbered 1 to 54, we can track the effect of a move on the cube by seeing how the numbers swap places. Doing my quarter-turn we see that facelet 1 goes to the position previously occupied by facelet 37, facelet 2 goes to the position previously occupied by facelet 38, and so on. When doing serious maths, to avoid constantly typing the phrase “goes to the position previously occupied by”, we might write this as

\[ \scriptsize{\left( \begin{array}{ccccccccccccccccccccc}
1&2&3&37&38&39&27&26&25&46&47&48&34&36&30&28&35&33&29&31\\
\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow\\
37&38&39&27&26&25&46&47&48&1&2&3&36&30&28&34&33&29&31&35\end{array}\right).} \]

If we’re feeling particularly terse (we always are) we might write that even more compactly as

\[ (1\ 37\ 27\ 46)(2\ 38\ 26\ 47)(3\ 39\ 25\ 48)(34\ 36\ 30\ 28)(35\ 33\ 29\ 31) \]

Here we start with $1$, which goes to the position previously occupied by $37$, so we look at $37$ next, and so on. If we get back to the number we start with we put brackets round that cycle and start again with the smallest number we haven’t looked at yet. (We know this will form separate tidy cycles for basically the same reason we know the states of the cube form a cycle.)

So we got the stickered cube, squinted at a number, twisted or turned the cube and worked out whose position that number took over. Doing so we arrived at the cycles for both the twist and the spin:

\begin{align} \mathrm{twist} &= (1\ 37\ 27\ 46)(2\ 38\ 26\ 47)(3\ 39\ 25\ 48)(34\ 36\ 30\ 28)(35\ 33\ 29\ 31) \end{align} \begin{align} \mathrm{spin} &= (1\ 3\ 9\ 7)(2\ 6\ 8\ 4)(25\ 27\ 21\ 19)(20\ 22\ 26\ 24) (12\ 54\ 34\ 37)(11\ 51\ 35\ 40)(10\ 48\ 36\ 43)(13\ 47\ 33\ 44)(14\ 50\ 32\ 41)  (15\ 53\ 31\ 38)(16\ 46\ 30\ 45)(17\ 49\ 29\ 24)(18\ 52\ 28\ 39). \end{align}

The twist moves four strips of three numbers round in little cycles of four, and the eight outer squares on the twisted face move in two more cycles of four. The spin has a more far-reaching effect, changing the position of every sticker except the two at the ‘poles’ of the rotation, $5$ and $23$.

Once you have two moves written down in this way, it’s easy to see the effect of one move followed by another: you just work out what happens to each number in turn. So the first move takes $1$ to the original position of some other number, call it $n$ ($n$ itself has of course also moved elsewhere). Where does the second move now take $1$? Well we know where it takes $n$ on the solved cube, and we know $1$ is now in that position, so the move now takes $1$ to whatever position it takes $n$ to in the solved cube. Once we’ve done this for every number,we’ll have written down the combined twist-and-spin move in the same form as above.

From this we can work out how many times it would need to be repeated to get back to the start. This last step shows the power of the cycle-based notation. A single cycle of length $n$ just needs to be repeated $n$ times so that every number shuffles back to its original position. And since none of the cycles interfere with each other, the number for a whole move is just the smallest number that’s a multiple of the lengths of all the cycles. Once we’ve found this, we’ll have the number of repeats needed to get the cube back to solved. What’s more, we’ll have worked it out without even having to actually do the two moves over after the other, let alone repeat them again and again. It doesn’t matter how ridiculously high the number turns out to be, we can get the answer with the same moderate amount of effort.

Although, as I’ve explained, it’s relatively simple to work out the number of repeats needed from this information, needing one slightly laborious calculation to get the sequence for the combined twist-spin, and a quick comparison of the lengths of the cycles, we instead plugged the cycles into a computer program. We used MAGMA, which is designed for doing calculations in the areas of maths that this is a pretty simplistic example of. You can try this yourself by pasting the below code into the online MAGMA calculator:

G:=Sym(54);
twist:=G!((1,37,27,46)(2,38,26,47)(3,39,25,48)(34,36,30,28)(35,33,29,31));
print "Order of twist";
Order(twist);
spin:=G!((1,3,9,7)(2,6,8,4)(25,27,21,19)(20,22,26,24)(12,54,34,37)(11,51,35,40)(10,48,36,43)(13,47,33,44)(14,50,32,41)(15,53,31,38)(16,46,30,45)(17,49,29,42)(18,52,28,39));
print "Order of spin";
Order(spin);
print "Order of twist*spin";
Order(twist*spin);

Plugging this into the computer gives the answer, which is 1,260. If you were doing serious maths you would call this the ‘order’ of the move sequence, as you can see from the name of the command used above. I find it pretty astonishing that two moves that individually each only need to be done four times to return to the initial state can get that much bigger when combined. This raises the obvious question: what’s the highest number of times that any sequence of moves would have to be repeated to return the cube to its initial state? Well we can find that out too, but first: a technicality!

One of my moves was to rotate the whole cube a quarter-turn. Well, some people might argue that that isn’t a proper move – I didn’t really change the cube. I may as well have sat it on a table and myself walked round to a different side. These purists would rewrite my two-move sequence as a four-move one: twist the front face, then the right face, then the back face then the left face. This four-move sequence still takes 1,260 twists to solve itself, but that’s now ‘just’ 315 repeats of the sequence. (A technicality within a technicality: if I’m counting rotating the whole cube as a single move, do I count a solved but rotated cube as being back in its initial state? I guess I shouldn’t – luckily this doesn’t arise with my sequence of moves. But probably best to stick with the purists’ view from now on.) It’s a little disappointing that we’ve had to drop from the impressive-sounding 1260 to a mere 315, but in our new system we can more easily determine the highest number of repeats possible.

If you’re going to tackle a question like this, it helps to have some notation worked out so you can talk about things like “a quarter twist of the front face clockwise and then a quarter twist of the back face anticlockwise by which I mean anticlockwise if you were round the back looking at it which is sort of clockwise when you do it by reaching round from the front” without needing to go and have a lie down. Luckily, many of the first people to seriously tackle Rubik’s cubes were mathematicians, so this is not a problem. The standard notation is now to use the letters $F$, $R$, $L$, $B$, $U$ and $D$ to denote a quarter twist of the front, right, left, back, top (up) and bottom (down) faces respectively (clockwise from the point of view of someone looking straight on at that face). Sequences of moves are just written as the corresponding sequence of letters, so my move was $FRBL$. A half-turn of, say, the front face can be written $FF$ (since it’s just two quarter turns) or more snappily as $F^2$. Since a quarter-turn anticlockwise is three clockwise quarter-twists, and is also the inverse of the clockwise quarter-twist, we can write it as $FFF$, $F^3$ or $F^{-1}$ (for “the inverse of $F$”).

The six lettered twists comprise a complete basic set of Rubik’s cube moves: everything you can do on the cube can be considered to be a sequence of these six moves. So if we tell a computer the permutations for these six moves, and if our computer is smart enough, it can tell us what combination of these has the longest ‘repeat time’. This is trickier than I’ve made it sound: effectively you have to work out the entire structure of the group of all sequences of moves and how they interlock. But if you do this, you find that the most repetitions any sequence needs is a familiar number: 1,260. One such move consists of five twists of various faces (four quarter-turns and one half-turn), written $RU^2D^{-1}BD^{-1}$. At a couple of seconds per twist, doing this sequence would take three-and-a-half hours to solve the cube. Still, this move is a little elaborate, and the random move-sequence I tried got pretty far up the scale of futility. In fact 315 is the best you can do with a sequence of up to four of the basic moves, so I claim a small victory for idly toying with objects as a means of uncovering some of their deeper mathematical structure.

287 Responses to “How to solve a Rubik’s Cube in one easy step”

  2. Avatar fatima

    If we spin it in the same position like shown in the video will it come to its original state

    Reply
  3. Avatar mgelo

    @ fatima: yes it will.

    In fact, the process of repeating the same basic sequence is a way to construct moves that only touch a small group of cubies. (I believe this is the term for the little cubelets that make up the Rubik’s cube.) For example, doing $F^2 R^2$ three times is a famous way to exchange two pairs of 2-colored cubies.

    “315 is the best you can do with a sequence of up to four of the basic moves”
    A more difficult question is: what is the absolute top bound?
    I wonder if an answer can be achieved using group theory. I recall there was a lot of this stuff done in the 1980s.

    Also, “solve” usually means bring the cube to order from a given (messed-up) state.

    I also like using brackets (if you noticed).

    Reply
    • Avatar Anonymous

      Okay first of all stop talking geek these are only kids trying to solve their Rubik’s cubes I’m pretty sure I’m the only other person who understands what your talking about like I said they’re only KIDs not geeks like you and me.

      Reply
      • Avatar Anonymous

        Be nice, some kids do understand what “geek” says, some might not. It’s life, deal with it.

        Reply
  4. Avatar Tudor Timi

    Since you’re dissecting the mathematics of Rubik’s cube, I have another question. At how many faces do I have to look at to guarantee that the cube is solved without looking at the rest?

    What I mean is, having 1 of the 6 faces solved does not mean that the other 5 are solved as well; they may still be shuffled. The same way, having 2 of the faces solved does not mean that the other 4 are solved as well.

    Just looking at 5 faces and seeing them solved will, however guarantee that the 6th is also solved. Is the same true for 4 faces or 3?

    Reply
    • Avatar Keith

      If you can only see four faces there are ways the other two faces might be incorrect. If the two faces are adjacent, the edges can be wrong. If they are opposite, the centres could be wrong.

      Reply
      • Avatar Samuel Noble

        While this might appear true at a first look, it isn’t.

        A minimum of four centers can be in disorder at a time. The centers are physically linked in an immutable way.
        Also, a single edge piece- can not by itself be in disorder. If flipped, there must be another flipped as well. If switched, there must be at least two others also switched.

        However, you are right to say that four sides is not sufficient to determine success:
        Looking at the cube in the photo above (the one in which numbered labels were attached). Imagine that Green and Orange are the unseen sides, and all the rest are solved. Faces 11 and 51 could be switched without your knowledge, as could faces 17 and 49. The same principle holds true if the unseen sides are opposite.

        Reply
  5. Avatar Katharine

    This is a fascinating application of math to every day objects. Most people don’t notice that everything is an equation.

    Reply
  7. Avatar Thomas

    Those are not brackets, they are parentheses ( ). These are brackets = [ ]

    Reply
        • Avatar Christian Perfect

          () are also called parentheses, but they’re more often called brackets. So we use “parenthetical”. If you’re looking for consistency, English is not the right place to look.

          Reply
          • Avatar Paul Taylor

            You’d also call a statement parenthetical if, like this one, it’s enclosed by commas or dashes. The punctuation marks which we may or may not call ‘parentheses’ are named after the sort of clause they contain rather than the other way round.

          • Avatar Samuel Noble

            While English doesn’t have a simple set of rules, there are very few exceptions to the vast set of complex regulations.
            I don’t have this on any authority, but in my experience and to the best of my knowledge, each “inconsistency” is actually just subject to a very specific rule that doesn’t have many application.

            For example:
            “I before E, except after C”
            Recently, people have added:
            “Or when making ‘eɪ’, as in neighbor or beige.”
            (Note: ‘eɪ’ is the phonetic description for English’s ‘long A’ sound).

            Other exceptions include ‘society’ and ‘science’, both of which can be pointed out as a rule in which the clever little rhyme above does not apply because the I and the E are con part of the same syllable.

            Yes, English is weird, complicated, and unintuitive, but I do believe it is mostly consistent.

            PS: In case you think you’ve caught me with one of the words in the last remark, know that it actually can be traced back to an Old English version that had two syllables, fitting into one of the rules above and one other major rule: everything in English is inevitably abbreviated, slurred, or otherwise shortened over time.

  9. Avatar Ted Berenyi

    An interesting discussion.
    However, your two basic assumptions make the problem much simpler.

    1. The unsolved cube was first obtained by a finite sequence of your “transformations” from the pristine “solved” state of the cube.

    2. The transformation is reversible.

    Hence, you can solve the cube by a finite sequence of the inverse transformation.

    Reply
  10. Avatar Ishan

    Do you mean that if we repeat the same steps again and again, starting from a solved cube, we will get a solved cube again?

    Reply
    • Avatar Ted Berenyi

      Yes, that is what this means. I wouldn’t really call this “solving” the cube. Given any unsolved cube with no knowledge of how it was obtained, this would not help to solve it. It solves a very special case whose solution is obvious anyway. It is never the less interesting.

      Reply
  11. Avatar Art W

    Thank you for the article! Ever since I was the kid in 80s I wondered if this kind of quarter turning can get the cube back to the solved state. I think the highest I got before giving up was about 200 turns. Now I know the answer: 1260.

    Reply
  12. Avatar omkar

    i am also with the 11 year old !!!
    i got nothing ! even though i am 15!!!!

    Reply
  13. Avatar Anonymous

    nooo it goes back keep on dooing it it does a lot of loops then goes back its called a trigger

    Reply
  14. Avatar RubiksCube

    Does anyone know an easy way that truly works properly in 2 moves and 1-5mins for an 11year old

    Reply
  20. Avatar Rob

    No this is not right, if you spin and twist the cube, the top face will eventually come up again, after I think 72 moves, the whole cube will be done again after 6 of these, 72 * 6 does not equate to 3 billion, therefore only a fraction of the possible combinations are possible with this one move. Try it, it takes about 15 minutes.

    Reply
  23. Avatar aash

    I can solve the cube without following any particular algorithm. I just search for the color that is needed to be matched and rotate that column remembering the colors that are going to be disturbed. Doing the same I manage to solve the cube each and every time.

    Reply
  26. Avatar Person

    Wow! This is truly fascinating. What a mind-blowing concept, and yet it makes so much sense. :)

    Reply
  27. Avatar FIDHA FATHIMA R

    I AM 10 YEAR ‘s OLD.
    I AM STUDYING SANATANA DHARAMA VIDYASALA ENGLISH MEDIUM SCHOOL.
    AT ALAPPUZHA .
    MY HOME WAS KAIJOONDI JUNCTION.
    I BUY RUBIX WHILE I HAVE 8 YEAR’s OLD.
    BUT I CVAN DO IT !!!!!!!!!!!!!!!!!!!!!
    I DO ONE COLOUR AT ONE TIME.
    THIS IS NOTHING . I DIDNOT UNDERSTAND THIS.
    ANY LIKE THIS ?
    PLESE REPLAY
    WITH YOUR ADRESS……………………………………

    Reply
    • Avatar abhijay

      im 6 years old and i can solve the rubiks cube in 1 second litraly i just do 1 thing and it solvves the intire rubiks cube

      Reply
  39. Avatar Michael

    GOT STUCK!!!!
    I wasn’nt able to get the white corners and match em’ with the centre………..
    …………..DIDNT WORK AT ALL.
    USE LESS ALGORITHMS

    Reply
  45. Avatar Sebastian Ramos-Roux

    This is stupid. I can do a rubiks cube in 45 seconds using algorithms from any scrambled state whereas this can only be used on a solved cube and isn’t really solving it. For that matter, turn one side 4 times and you also have a “solved” cube.

    Reply
    • Avatar Mya

      Me too. All i understand is that the dumb stupid video ruined my rubix cube. I had one side done but then i thought the video showed you how to complete it so now i have to figure out how to complete one side again thanks to that stupid video!

      Reply
    • Avatar Mya

      its not easy, but someone on my bus can do the rubix cube in 8 seconds and hes in 3rd grade. Im in 5th grade and i cant even do it. And im awesome at solving puzzles. One time i solved a puzzle in 6 hours in one day and its a 500 piece puzzle. If i can do that, im sure that i could solve the rubix cube but i cant

      Reply
    • Avatar Diptoneel De

      OMG!The king of cubing on such an amateur website!
      Well I live in India and average around ~70 secs.But you do it in just ~6 secs!Even though I use Cfop with algorithmic F2L and 4LLL,the move goes very high,around 110moves.Please help and suggest.

      Reply
  57. Avatar Feliks Zemdegs

    Which means F2L, FL2, FL2, F2L. If you do that algorithm 5-6 times, than your cube will be solved, ( any cube ). Try it guys, you can start from any position, pick up your cube THE WHITE TOWARDS YOU AT ALL TIMES, and start from scratch, I hope you guys do well in solving it.

    Reply
  59. Avatar Mya

    the only thing that i can complete is one side only i all ways do the white side first but then when im done with the white side i cant do anything else. But someone on my bus when i go to school in the morning, someone in 3rd grade can complete the rubix cube in 8 seconds

    Reply
  61. Avatar Anonymous

    This is sooooo confusing! (-_-) (-_-)
    \( (> <) )/
    / \ / \
    all the single ladies, all the single ladies…lol

    Reply
  70. Avatar Anonymous

    I don’t get this and I’m 10 1/2 years old and a girl so that doesn’t mean that girls are always smarter than boys and all these comments I’ve read make sense but then I don’t get the other comments Don make any sense so yeah I have a rubik’s cube so if u think breaking the rubik’s cube is cheating I don’t because I was so fist rated when I couldn’t do it

    Reply
  71. Avatar Peter

    I just learned how to solve it regularly, it’s fun and I can solve it in 25 seconds on average.(personal best is 18.563)

    Reply
  73. Avatar Kazuki

    The Rubik’s Cube is an amazing puzzle. It just takes practice and practice and practice. You just need to get used to the mindset. I’m 14 but anybody can learn. Just play with it, trying different patterns from its solved state. If you mess it up, you can always just take it apart and put it back together lol

    Reply
    • Avatar Dodo

      Im nine and this is harder then anything iv ever done
      (You guys make no sense) oh how old is the guy who said he was a month old???????
      Sorry i mean 3 moths old.

      Reply
  78. Avatar Kale_b

    I can solve a ruby’s cube regularly, but I’m trying to find a way to solve it in under 40 seconds. This makes no sense what so ever. Not even what I asked for

    Reply
  79. Avatar Malachi Clifton

    I’m 17 (apparently that matters). I have over 15 cubes (only like 3 of which are 3x3x3s). My record on a 3×3 is 45 seconds which is not terrible fast but not worthy. When I’m bored I sit around messing with my cube figuring out patters and logic. This entire post made complete sense, the writer clearly is very smart bit does not actually know how to solve a cube. In his video he is doing hi “algorithm” the hard way, but it still works. I really like how he mathematically calculated it but he must have missed something in his calculations . He is exactly 60 short, which is interestong because after sixty of these moves the top of the cube solves and it takes exactly 22 of these sets of 60 to solve it. I have counted it many times. Somehow he came up with 21 which makes no sense because cubes resolve after doing a repetitious algorithm in round even numbers that can in some way be divisible or multiples the amount sides, species and or the sides being moved.

    Reply
  80. Avatar Malachi Clifton

    I would like to correct my incorrect counting from my previous comment, since then I have redone this and realized it is actually 21 sets of 60 which is 1260.

    Reply
  83. Avatar poo

    Liam
    May 23rd, 2016

    age is just a number

    false! Age is the amount of times you’ve been around the sun. hahahahahahahahaha!!!!!!!!!!!

    Reply
  85. Avatar Diptoneel De

    So easy!Better learn the standard method to solve it.I’m just aged 13 now but,after 4 months of practice,I can solve it under 80seconds

    Reply
  88. Avatar Wonder Woman

    Yeah I’m 11 and I don’t understand a thing, well bits of the first half anyway. :-(
    I agree it is quite boring.

    Reply
  89. Avatar Edgar

    I dont really get this. ..just one thing that i kinda get and will ask is; this steps only work wgit a rubiks cube that is already solved right? Or will it also work with one that is scrambled??

    Reply
    • Avatar Paul Taylor

      If you start with a scrambled cube, it will go through its own cycle of 1260 positions and return to the scramble you started with. That cycle of 1260 positions won’t have any positions from the “main” cycle in it (except if by a massive coincidence you started with one of the scrambled positions in the main cycle, in which case you’ll go round the main cycle but starting in a different position).

      Reply
  92. Avatar Pat

    I am 12 and i know how to solve a rubies cube in 28 seconds! This is true but you have to do it from the when you have the rubies cube already finished and done so this can’t really help any of you that don’t know how to solve one! sry!

    Reply
  97. Avatar dusty

    please help i suck im 13 and still cant solve mine and ive been working on it since i was four

    Reply
  100. Avatar Anonymous

    hoooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooow!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!DO YOU SOLVE THE CUBE!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

    Reply
  104. Avatar Anonymous

    i’m 5 year old and i understand everything
    But the method deviates little bit form my primary solution to this equation

    Reply
  105. Avatar the great sean

    Im 5 and I understand everything.
    Well I would like to say the method deviates little bite form an easier path to the primal solution to this equation.
    Thank you.

    Reply
  108. Avatar Anonymous

    I don’t understand thus bullshit of a method. I tried it and it doesn’t work. I woukd not recommend this stupid shitty ass method on how to solve the method. NO ONE TRIED THIS METHOD AT ALL THE PERSON WHO MADE THIS METHOD I A FRAUD AND A LIER DON’T LISTEN TO THEM

    Reply
  110. Avatar Carlako

    > needing one slightly laborious calculation to get the sequence for the combined twist-spin

    But then again, maybe it’s just on-par with the initial work done to write out the cycles for the spin!

    If you combine the two moves you listed:

    [twist]
    (1 37 27 46)
    (2 38 26 47)
    (3 39 25 48)
    (34 36 30 28)
    (35 33 29 31)

    followed by:

    [spin]
    (1 3 9 7)
    (2 6 8 4)
    (25 27 21 19)
    (20 22 26 24)
    (12 54 34 37)
    (11 51 35 40)
    (10 48 36 43)
    (13 47 33 44)
    (14 50 32 41)
    (15 53 31 38)
    (16 46 30 45)
    (17 49 29 24)
    (18 52 28 39)

    you get

    [twist+spin]
    (1 12 54 34 43 10 48 9 7)
    (2 15 53 31 40 11 51 35 44 13 47 6 8 4)
    (3 18 52 28 37 21 19 25 36 45 16 46)
    (14 50 32 41)
    (17 49 29 38)
    (20 22 26 33 24)
    (27 30 39)

    If you count, these independent cycles have lengths:
    9, 14, 12, 4, 4, 5, and 3.

    In prime factors, that is:
    3*3, 2*7, 2*2*3, 2*2, 2*2, 5, and 3

    The cycle will repeat when all the independent cycles meet up, which is the least common multiple of all the independent cycle lengths. Which is the product of maximum power of each prime across all the cycles:
    2*2 * 3*3 * 5 * 7

    Which is your 1260.

    Reply
  112. Avatar Anonymous

    I don’t understand it one bit I’m 11 years old and it’s like stupid cause they just show you what it looks like but they don’t really help you and it’s annoying and I don’t get it so they suck

    Reply
  114. Avatar Genuis

    I’m 13 and I understand this. If you read the whole thing it makes sence.

    Reply
    • Avatar niko

      its been a while since ive last been on here. you literaly don’t have to pay attention to this website to solve a Rubiks cube. there is no alorithm to solve any rubiks cube at any time. however, if you have extreme skill, the mind of a robot, you can easily solve any rubiks cube in 24 moves or less. ive been able to solve a 3×3 rubiks cube for years now. the best way to do it is by this link https://www.rubiks.com/media/guides/RBL_solve_guide_CUBE_US_5.375×8.375in_AW_27Feb2020_VISUAL.pdf. its the most basic way to solve a rubiks cube, but it still takes tallent. as time goes on, you can move onto the cfop meathod. im still learning some of the cfop meathod, so i can solve a rubiks cube significantly faster that i used to. my record is 38 seconds, so once i learn all of the cfop i can solve it faster. the world record is 3.47 seconds, so ill never get there. if anyone can find someone who knows how to solve a rubiks cube in 24 moves or less, contact me at dominik.nebelski@gmail.com so that i can hopefully train them to break the record.

      Reply
  118. Avatar AB

    I’m think there’s a flaw in your impossibility of loops argument. You are assuming that the loop repeats after a complete (integer) set of the original moves. But there’s nothing stopping it from completing a loop after a fractional number of steps, i.e. the last step need not complete the original move but end part way. Then you don’t have a paradox.

    Reply

(will not be published)

$\LaTeX$: You can use LaTeX in your comments. e.g. $ e^{\pi i} $ for inline maths; \[ e^{\pi i} \] for display-mode (on its own line) maths.

XHTML: You can use these tags: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>