Ten! TEN! TEN! Incredible. David Cushing asked me a very good question once: what have you done between five and ten times (inclusive)? Well, this is the last time ‘Writing an Aperiodical Round Up’ will be in the same category as ‘getting a new wallet’ and ‘saying hello to Peter Beardsley’.
Hello, my name’s Christian Perfect and, more often than an unbiased observer would expect, I find odd maths things on the internet.
A while ago, I went through a phase of noticing mathematically interesting times more often than I thought was reasonable. For example, there’s a great run of times from 12:34 to 12:36:
- 12:34 is an arithmetic sequence of digits
- 12:35 is the first four Fibonacci numbers
- 12:36 is interesting because $1 + 2 + 3 = 6$, $1 \times 2 \times 3 = 6$, and $12 \mid 36$.
And it felt like I’d suddenly started noticing them happen every day.
Of course, this digit-rich instance of the Baader-Meinhof phenomenon leaves me only a pinch away from the undiluted crazy-juice of numerology. One class of ‘interesting’ times is the repeating digits: 3:33, 22:22, and so on. It turns out some sad saps have taken to calling the members of A010785 “Angel Numbers”, because angels are… noted for their repetitive nature or something?
Joanne at Sacred Scribes has a big long page listing the messages and meanings behind the numbers from 0 to 1700. Don’t let the fact that there are only 29 repdigits below 1700 put you off: clearly a number such as 433 is just the concatenation of the angel numbers 4 and 33, and is hence
a combination of the vibrations and energies of number 4 and number 3, with number 3 appearing twice, amplifying its influences and resonating with the Master Number 33.
Uri Geller has a page about how it always seems to be 11:11. Spurious claims abound, including this particularly fishy revelation:
HOWEVER, if you count the fingers on your hands in unary arithmetic – no zeros – then 10 fingers, in unary mathematics, = 11111111111 – EXACTLY 11 ONES
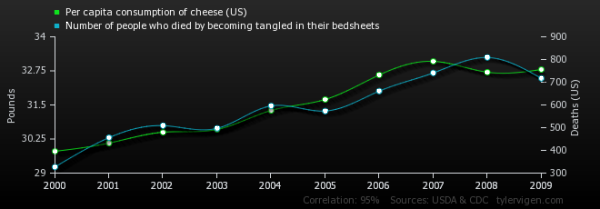
Talking of spurious claims, Tyler Vigen has downloaded a load of historic statistics from the US, and compared them all against each other to find Spurious Correlations. For example, did you notice that per capita consumption of cheese correlates very strongly with the number of people who die by becoming tangled between their bedsheets? (don’t say Winsor McCay didn’t warn us)
If you’d asked me before I wrote this paragraph to give a criterion for an interesting collection, I would’ve said that its individual elements had to be interesting on their own. But that rules out House of Leaves of Grass, a ten trillion-stanza poem generated by combining lines from Leaves of Grass by Walt Whitman and House of Leaves by Mark Z. Danielewski. It makes creative use of the bijection between mouse co-ordinates and an enumeration of the combinations of lines.
Now, I’m a big fan of encyclopedias and collections, and I’ve written here in the past about collections of interesting numbers. But there’s so much more to collect! There’s a bit of my brain that gets excited when I come across a new collection, whether it’s minimal sudoku puzzles, or unsolved problems. People studying topology like to use counterexamples to prove or disprove theorems about properties of spaces. That means there’s a market for collections of counterexamples! There’s the venerable book Counterexamples in Topology, but this is the twenty-first century and I want a refund if there aren’t at least two similar collections freely available on the internet.
π-base and Spacebook are databases of topological spaces, searchable by properties and packed to the gunnels with proofs and references.
But what if you could boil down all the knowledge and facts contained in these collections into a sheet or two of A4 paper? That’d be really convenient. László Kozma has collected what he reckons are some of the most useful mathematical inequalities into a handy cheat sheet. I can’t think how it would ever be useful, but I’m considering putting it up outside my office to scare the students during the exam period.
Poetry can involve maths in ways other than its composition: Patrick Stevens’ slightly silly Sylow pseudo-sonnets use a variety of poetic forms to state the Sylow subgroup theorems in a way that could easily be set to music – cough cough Herbert Gangl.
Next, I’ve got some things about graphs and some things about books, and I’m not sure which should go first.
I’ll go with books, because poetry usually happens in books and I like to have some continuity between my topics. There’s a thing called the New Books Network, and it has a section for new maths books. It’s a podcast of interviews with the authors of maths books. The books that have been covered so far all fit pretty well in to the “popular maths” mould.
What’s the opposite of popular maths? Unpopular maths! There’s a place called MathSciNet, where mathematicians review other mathematicians’ work. Normally they provide an overview of the work under consideration and some comments on the work in context but, in exceptional circumstances, the reviewer gets their claws out and rips the author a new one. Kimball Martin’s list of Exceptional MathReviews collects these lapses in scholarly propriety for your amusement.
If your disagreement with a work is so great that you can’t confine it to a snotty MathSciNet review, what else can you do? If you’re Peter Luschny, and you’re taking on both the Handbook of Mathematical Functions and Knuth’s Concrete Mathematics, you need to lay out your case on a nicely-presented page with lots of graphs and equations and pictures of historical luminaries, in your Bernoulli Manifesto.
Historical mathematicians are very moreish. Here, have Some Mathematical Works of the 17th & 18th Centuries, including Newton’s Principia, Euler’s Mechanica, Introductio in Analysin, etc., translated mainly from Latin into English, by Ian Bruce.
How long did Goodnight Moon take? The answer may shock you/surprise you/not be well-defined!
Now graphs. Did you know that Marvel Entertainment maintains a huge database of every bit of information they’ve ever invented about their characters, and uses graph theory to “understand, model and ultimately represent the uncanny Marvel Universe”?
By the way, did you know that Marvel Heroes Math Made Easy is a book that exists and can be bought? I didn’t. What a marvellous thing that is.
Here’s something else you probably didn’t know you could buy: packs of post-it notes with graph grids and axes printed on them, for those occasions when you need to stick a precise function plot on something. What could that something be? Maybe one of Michael Punzak’s models of the addition and multiplication tables. That would really math it up a notch.
Somehow, I’m still not done with my graph links. The online graphing calculator Desmos has a page of artistic graphs. For example, here’s a Road Runner.
The Wellcome Collection recently put all its stuff online for the public to view. Obviously, the first thing I did was look for pictures with some maths in. Here’s what I found:
- Man giving geometry lesson
- Castle maths
- Professor Maths and his students
- Pascal’s calculating machine
- Graph plotter
- Compass set, in new X-Ray Vision™
- Mechanicks cheat sheet
- Cherubs at war
- Let Geometry help!
That diagram of Pascal’s calculating machine should have piqued your curiosity. I’ve tracked down this nice video explanation of how it worked for you. De rien, don’t thank me!
[youtube url=https://www.youtube.com/watch?v=3h71HAJWnVU]
The Florida Center for Instructional Technology has a lovely collection of mathematical clip-art. I particularly like the “Math Tools” section.
 This appears to be the arts section of the post, so I’ll leave Martin Probert’s page on The Survival, Origin and Mathematics of String Figures here. I’ll be back to pick it up at the end. Maybe it’d like to play with Steven H. Cullinane’s pages on the Finite Geometry of the Square and Cube.
This appears to be the arts section of the post, so I’ll leave Martin Probert’s page on The Survival, Origin and Mathematics of String Figures here. I’ll be back to pick it up at the end. Maybe it’d like to play with Steven H. Cullinane’s pages on the Finite Geometry of the Square and Cube.
Recently on the SeqFan mailing list, the mailing list for fans of integer sequences, Neil Sloane asked about the number of arrangements of $n$ lines in the plane, and Jon Wild responded with this fantastic document of diagrams showing distinct planar configurations of $n$ circles. If an arty maths person doesn’t turn those into a polyptych of some sort, I’ll be sorely disappointed.
There are a few very short sequences in the Online Encyclopedia of Integer Sequences. Some of them only have a couple of known members, but are conjectured to be infinite. It can’t be a coincidence that so many of them have names starting with the letter W. I can only assume that’s why the Wieferich, Wilson, Wall-Sun-Sun and Wolstenholme search is tackling those sequences together. The intrepid leaders of the search wrote up some preliminary results a few years ago; in case you’re wondering where to start your search, they report that there exist no such primes $p \lt 2 \times 10^{14}$.
So those sequences are very hard to compute. The easiest sequences to compute (literally?) are recursive sequences. Tanya Khovanova has made a gloriously expansive page collecting all the recursive sequences she can find.
I’m going to end with some software. Of course, that means I’m going to show you a cellular automaton, but don’t worry: this time I don’t care if it’s Turing complete. Panic Shooter is a shoot-’em-up which takes place inside a cellular automaton. Groovy!
Some hoopy froods in Germany have made a program which tells you how to make any 3d model out of Zometool. Disappointingly, they have not yet made a Zome gnome.
swMATH is a search engine for maths software, offered by the same people who made zbMATH, which is a bit like MathSciNet but without the catty reviews (as far as I know).
So that’s the end! I’ve got just one link left for you. Do you know about numbers stations? They’d just transmit numbers all day, for spies to use. That’s right: numbers! On the radio! A mathematician’s dream! But they don’t really exist any more, which is sad.
Well, someone has recorded a load of grime music stations and edited them down to just the good bits. I present to you the Grime Numbers Station:
[soundcloud url=”https://soundcloud.com/autodespair/grime-numbers-station-mp3″]
It’s transfixing, like a version of Sailing By from the world where mathematicians get their way.



2 Responses to “Aperiodical Round Up 10: a rathole down which valuable mathematical effort is being poured”