Bees have encouraged mathematical speculation for two millennia, since classical scholars tried to explain the geometrically appealing shape of honeycombs. How do bees tackle complex problems that humans would express mathematically? In this series we’ll explore three situations where understanding the maths could help explain the uncanny instincts of bees.
Honeycomb geometry

A curvy wild honeycomb.
Honeybees collect nectar from flowers and use it to produce honey, which they then store in honeycombs made of beeswax (in turn derived from honey). A question that has puzzled many inquiring minds across the ages is: why are honeycombs made of hexagonal cells?
The Roman scholar Varro, in his 1st century BC book-long poem De Agri Cultura (“On Agriculture”), briefly states
“Does not the chamber in the comb have six angles, the same number as the bee has feet? The geometricians prove that this hexagon inscribed in a circular figure encloses the greatest amount of space ((Translation by Hooper and Ash in the Loeb. I’ve been told that ‘Hexagonon’ is in its singular form, and the only Greek word (also having Greek grammar) amongst this part of Varro’s Latin text. I would be happier that Varro understood what he was writing about if the text more explicitly described the construction, perhaps ‘Three hexagons encircling a point’, or ‘Six hexagons arranged around a seventh’. In translation, it could be viewed as falsely suggesting that the hexagon is the polygon with the greatest area that fits inside a circle. In his defense though, Varro also earlier suggests that orchards be arranged regularly in quincunxes, the arrangement of spots representing the number five on dice, to take up less room and give better quality produce. The centres of hexagons in a regular hexagonal tiling can be thought of as an elongated quincunx, repeated. As this is essentially the same result used in another context, I’ll give Varro the benefit of the doubt and defer to Varro’s poetic license.)).”
This quote is the earliest known source suggesting a link between the hexagonal shape of the honeycomb and a mathematical property of the hexagon, made more explicit a few centuries later by Pappus of Alexandria (sometimes considered to be the last Ancient Greek mathematician). Writing after the Roman Empire’s glory days, 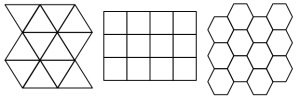 Pappus points out that there are three regular polygons that tile the plane without gaps—triangles, squares and hexagons—and bees, in their wisdom, choose the design that holds the most honey given a set amount of building material ((A translation by Ivor Thomas in the Loeb “Greek Mathematics: Volume II“, of a passage from Pappus’ Synagogue, Book V: “That [bees] have contrived this in accordance with a certain geometrical forethought we may thus infer. They would necessarily think that the figures must all be adjacent one to another and have their sides common, in order that nothing else might fall into the interstices and so defile their work. Now there are only three rectilineal figures which would satisfy the condition, I mean regular figures which are equilateral and equiangular, inasmuch as irregular figures would be displeasing to the bees
Pappus points out that there are three regular polygons that tile the plane without gaps—triangles, squares and hexagons—and bees, in their wisdom, choose the design that holds the most honey given a set amount of building material ((A translation by Ivor Thomas in the Loeb “Greek Mathematics: Volume II“, of a passage from Pappus’ Synagogue, Book V: “That [bees] have contrived this in accordance with a certain geometrical forethought we may thus infer. They would necessarily think that the figures must all be adjacent one to another and have their sides common, in order that nothing else might fall into the interstices and so defile their work. Now there are only three rectilineal figures which would satisfy the condition, I mean regular figures which are equilateral and equiangular, inasmuch as irregular figures would be displeasing to the bees ![]() . [These being] the triangle, the square and the hexagon, the bees in their wisdom chose for their work that which has the most angles, perceiving that it would hold more honey than either of the two others. Bees, then, know just this fact which is useful to them, that the hexagon is greater than the square and the triangle and will hold more honey for the same expenditure of material in constructing each.”)).
. [These being] the triangle, the square and the hexagon, the bees in their wisdom chose for their work that which has the most angles, perceiving that it would hold more honey than either of the two others. Bees, then, know just this fact which is useful to them, that the hexagon is greater than the square and the triangle and will hold more honey for the same expenditure of material in constructing each.”)).
The idea that bees economically choose the regular tiling polygon with the greatest area for a given perimeter satisfied the ancients. But why should all the honeycomb cells be identical—could bees do any better than using regular polygons?

The rhomboidal base of a wax foundation is behind the flatness of domestic honeycombs. Image from Creative Commons
The amazingly regular honeycombs we are used to seeing are built by domestic honeybees, using perfectly regular wax foundations provided by their beekeepers as a guide. Wild honeybees, however, don’t have the luxury of nestboxes fitted with wax foundations. Their honeycomb cells, though still very regular, aren’t always hexagonal—sometimes pentagons and heptagons creep in. After choosing an irregularly-shaped tree cavity, many worker bees will start independently building the hive’s hexagons at once, meeting in the middle along seams. It is along these seams where the five and seven-sided irregularities and other defects tend to appear ((Hepburn and Whiffler, “Construction defects define pattern and method in comb building by honeybees“, Apidologie (1991) observe that sometimes the pentagons and heptagons appear together, and at other times pentagons appear in clusters. They suggest that the latter can happen when a heptagonal comb is bisected by an extra wall, giving rise to two pentagonal cells.)).
More intriguingly, what happens if you provide honeybees with the wrong size of foundation as a guide? H. Randall Hepburn tried this with variously-sized hexagonal foundations ((H.R. Hepburn “Comb Construction by the African Honeybee, Apis mellifera adansonii“, Journal of the Entomological Society of Southern Africa, Vol.46, No.1, pp.87-101 (1983) ))(with flat bases unlike the standard ridged commercial ones). The largest caused the bees to to build gorgeous rosettes—they filled each large hexagonal foundation with five or six cells (again, typically five or seven-sided) surrounding a central cell. The next size down caused the bees to build in an irregular pattern, while the size smaller than that led to the bees building hexagonal cells on each vertex of the foundational hexagons, and leaving a hexagonal void or ‘false cell’ in the centre.

Cell construction by African honeybees on foundations of various sizes. ©Entomological Society of Southern Africa – reproduced with permission of the Society
So bees don’t necessarily need to use regular polygons at all. Allowing for the possibility of a mixture of shapes leads to two subtly different mathematical problems:
(P) Which mixture of shapes that tile the plane, and each have unit perimeter, have the maximum average area?
Fejes Tóth, a Hungarian mathematician, had proved by 1963 that the regular hexagonal tiling was the solution to the isoperimetric problem, (P), but only proved that it solved the iso-areal problem, (A), under the assumption that all the shapes were convex. This convexity condition is more restrictive than it may at first seem: a bulging edge on one shape leads to a concave indentation on a neighbouring shape, so the only convex shapes that can tile the plane are polygons.
It wasn’t until 1999 that Thomas Hales proved that hexagons also divide a plane into shapes of equal area with the least perimeter.
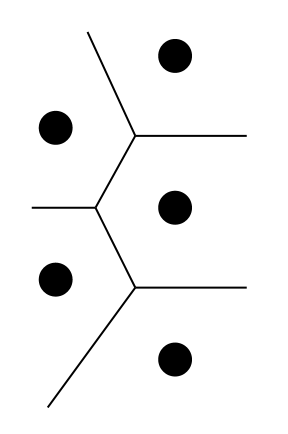
A key step in the proof (though not Hales’ breakthrough) is showing that, on average, such shapes would have six sides. Take a planar graph (ie. with no edges crossing) on a sphere. Using the Euler characteristic of a planar graph (which also holds on a sphere), we know that the number of the vertices, edges and faces of the graph satisfies $V-E+F=2$.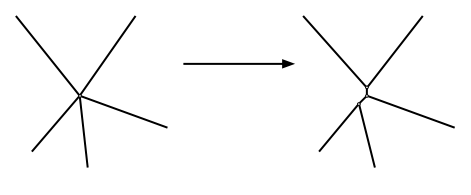 Nudging the edges slightly, it turns out to be sufficient to consider only vertices of degree 3. It’s quite easy to convince oneself with a diagram (like the one above) that this is plausible. Moving edges by a tiny amount, you can make sure no more than three lines meet at one vertex. You might change the numbers of edges and vertices, but without changing the perimeter or area by much.
Nudging the edges slightly, it turns out to be sufficient to consider only vertices of degree 3. It’s quite easy to convince oneself with a diagram (like the one above) that this is plausible. Moving edges by a tiny amount, you can make sure no more than three lines meet at one vertex. You might change the numbers of edges and vertices, but without changing the perimeter or area by much.
If the $i$th face has $e_i$ edges (and vertices), then adding these up for each face, we would count each edge twice and each vertex three times ((Explicitly, $V=\sum_i \frac{e_i}{3}$, $E=\sum_i \frac{e_i}{2}$, and $F=\sum_i 1$.)). So, by the Euler characteristic of the whole graph, overall we must have $$V-E+F=\sum_i \left ( \frac{e_i}{3}-\frac{e_i}{2} + 1 \right )=\sum_i \left ( 1 – \frac{e_i}{6} \right )=2.$$As the number of faces increases, $1 – \frac{e_i}{6}$ must become very small, and so the average of $e_i$ over all faces $i$ tends to $6$, which is the number of sides we were hoping for. ((This part of the argument was adapted by Hales from Fejes Tóth’s proof, except Hales used a torus instead of a sphere, which has the more computationally elegant Euler characteristic V-E+F=0.)) This step can be used to show a finite version of the theorem on the plane, which is a good start for the infinite version.
So out of all the prisms arranged side-by-side, hexagonal prisms use the least beeswax to build a unit bee-sized volume. But honeycombs are not made up of hexagonal prisms: the hidden end of the honeycomb cell is not flat. There are two layers of cells, back-to-back and offset, and the end-cap between them is a pyramid made of three rhombuses, so the whole shape could also be described as ‘half of an elongated rhombic dodecahedron’. The ridged wax honeycomb foundation pictured near the start mimics these rhombuses. This shape is more efficient than a hexagonal prism with a flat base.
What bees haven’t realised, is that there’s a slightly more efficient way to cap off their hexagonal cells. Keeping the hexagonal footprint of their hive, they could make repeated use of a truncated octahedron, formed by lopping off the vertices of an octahedron. This would lead to a saving of almost 2% in the idealised version with walls of negligible thickness, which isn’t much.
Using a curvy non-polyhedral variant of the truncated octahedron, Lord Kelvin, the 19th century physicist, held the record for ‘least surface area for a fixed volume’ in the three-dimensional version of the honeycomb conjecture for a full century ((On the Division of Space with Minimum Partitional Area, Sir William Thompson (1st Baron Kelvin), 1887 – given that the polyhedral truncated octahedron beats the rhombic dodecahedron anyway, I’m confused by what problem Kelvin claims is solved in his Yoda-like comment: “Certainly the rhombic dodecahedron is a solution of the minimax, or equilibrium-problem; and certain it is that no other plane-sided polyhedron can be a solution.”)). This was assumed to be the best possible until 1994, when two physicists, Denis Weaire and Robert Phelan, armed with computers, devised an ever-so-slightly more efficient way of dividing space into cells of equal volume, using two different curvy solids (2.2% more efficient than the rhombic dodecahedra). It was after this discovery that the long-standing two-dimensional honeycomb conjecture seemed less obviously true: a suggestion from Weaire is what nudged Hales to attempt his proof ((Weaire to Hales: “Given its celebrated history, it [the honeycomb conjecture] seems worth a try . . . ”)).
Despite the fact that honeybees do not achieve a theoretical minimum surface area for a set volume, honeycombs are still a sensible way to reduce the need for building materials. However, we should question the assumption that evolution is purely trying to economise on the bees’ behalf, and ask whether this actually is the main reason why honeybees build hexagonal honeycombs. Building a typical wild nest takes approximately a kilogram of wax, produced by consuming about eight times that amount of honey. Since this is also a third of the amount of honey the bees require to survive the winter, there is a strong evolutionary incentive to use as little wax as possible. There is evidence that bees do economise in another sense when building hives: they have some preference for nesting sites where honeycombs are already present ((Seeley and Morse, “Nest site selection by the honey bee, Apis mellifera” £29.95, Insectes Sociaux (1978) )), so they don’t need to build new ones. An alternative explanation to the economic argument is an engineering one: that hexagonal honeycombs are strong structures. It seems pretty hard to design experiments to determine how much each factor contributes to the bees’ motivations ((If the regular hexagonal array is both locally optimal for structural integrity as well as for wax conservation, then separating the two contributions is even more difficult)), so for the time being the explanations may well remain as Just-So stories.
One useful way of looking at the causes of a particular animal behaviour is to ask four questions, known as Tinbergen’s questions. The idea is to explain the current and historical reasons for a behaviour’s existence by asking questions about the individual and the species.
(Current & species: Function) Why have honeybees evolved to build combs in this shape?
(Historical & species: Phylogeny) How has honeycomb building evolved over time?
(Current & individual: Mechanism) How do the bees construct the honeycomb?
(Historical & individual: Ontogeny) How does the behaviour develop in an individual bee?
We’ve been looking at one possible answer to the first question, however this still leaves three unanswered. The ontogeny, or biological and neurological development of bees’ building behaviours is well beyond the scope of this article, which is convenient because I know absolutely nothing about it. As for the other two questions, Charles Darwin (among others) had a good crack at them.
Among the biological investigations recorded in Darwin’s “On the Origin of Species” were experiments and observations relating to honeycomb formation. He proposed that a rough evolutionary progression (the phylogeny) could be inferred from various types of modern bee nests. Bumblebee nests are rough conglomerations of almost spherical cells found underground. The nest of the Mexican stingless bee, Melipona domestica, lies somewhere between that of the bumblebee and honeybee, with a hexagonal arrangement but more rounded cells and cylindrical walls.
Looking at these other bee nests, Darwin suggested that honeybees once had nests similar to bumblebees, then more like those of the Mexican stingless bee, before their current honeycombs. Through conversation and correspondence, he came to the same conclusion as some others before him, that if bees built regular arrangements of cylindrical or spherical cells closer and closer together over the generations, then at some point they would crowd together into the famous honeycomb arrangement.
In more formal modern mathematical terms, this is the idea of Voronoi cells. Take some points in space: the region closer to one point than any other is known as that point’s Voronoi cell. If you take points in two slightly offset layers, all spaced equally to their closest neighbours (ie. joining the points would form equilateral triangles and hexagons), then the three-dimensional Voronoi cells form the honeybees’ hexagonal cells with their rhombic bases (partial rhombic dodecahedra).
Darwin wanted to know whether this theory matched up with the way bees actually build their hives. He watched very closely as his own honeybees constructed their nest and his observations support the Voronoi cell idea of how the nests evolved and how they are built. Darwin conducted some brilliantly simple experiments that involved introducing either a thick wax block or thin coloured wax sheet into a hive. With a wax block introduced, each bee dug a small hemisphere into the block, until it touched or got extremely close to an adjacent bee’s excavation, at which point the bees built the hexagonal walls up, leaving a smooth basin. This suggests that in the usual situation, the rhomboid basins are caused by pressures from bees working on cells on the other side, whereas in this case there were none. With a thin sheet introduced, the bees started excavating but stopped before they broke through to the opposite side, leaving very shallow and flat basins. This is all supports Darwin’s suggested mechanism for the cell construction.
In the classic 1917 book “On Growth and Form” D’Arcy Thompson points out that the beeswax is warm and slightly liquid when being used for building, which may cause tension effects to come into play. The same effects cause bubbles to naturally seek shapes that minimise their surface area. This is attractive as an alternative to the Voronoi cells idea, and so gets frequently repeated, but to me it doesn’t yet seem to be supported by the evidence.
The surface tension explanation is most vocally put forward in the paper Honeybee combs: construction through a liquid equilibrium process? (££) ((Pirk et al (£29.95), Naturwissenschaften (2004) )). The authors suggest that—in analogy with experiments where wax is melted around close-packed rubber bungs—the bees first construct cylindrical cells, and then heat them until the wax melts enough for surface tension to take over and form the hexagons. ((The paper also makes an interesting mistake, by remarking that the shape of the honeycomb base is rounded, and not rhomboid as usually described. This is based on moulds they made of the cells. It was later pointed out that they must have used old honeycomb cells, which gradually become rounded over time. The authors ascribed the previous rhomboid observations as either having been taken from cultivated honeycombs with wax foundations, or the straight-edges being an optical artefact from viewing two offset layers of hexagons. While being independent-minded and relying on your own observations is admirable, overturning several centuries of observations shouldn’t be taken lightly.))
A rebuttal, Hexagonal comb cells of honeybees are not produced via a liquid equilibrium process (££) ((Bauer and Bienefeld (£29.95) Naturwissenschaften (2013) )), points out some weaknesses in the paper above. The bees are seen to actively move their mandibles across the cell walls (video, 22mb AVI), mechanically shaping them, as well as feeling them with their antennas. Social wasps build their hexagonal nests with cellulose, a rather different material to wax. Cellulose doesn’t have the same fluid properties under heating either, so it is merely softened by the wasps using saliva. This means that wasps achieve similar results to the honeybees by actively kneading cells into shape without surface tension effects. If in doubt, we should prefer arguments that have more explicative power, and not resort to special cases for bees and wasps.
Central to the argument is the question of whether bees construct intermediate cylinders. This observation only seems to appear once in the literature, in a paper published in 2013 (after the above rebuttal) ((Karihaloo et al. “Honeybee combs: how the circular cells transform into rounded hexagons“, J.R. Soc. Interface (2013) )). This paper shows a close-up photo of the few circular cells found after the honeybees were smoked out during the construction of their hive. The circular cells were near the edge of the growing comb, a bit shorter than the usual 10mm, and the walls nearest the base of the circular cells were hexagonal. After the bees returned and completed their work, these cells were modified to their normal hexagonal specifications.
Unfortunately, this observation doesn’t clinch the argument either way. While it is necessary for surface tension to play a major role, intermediate cylinders are consistent with both explanations. The fact that bees rework their cells as the comb expands was noticed by Darwin, who observed that some vermillion-coloured wax introduced at the edge would become dispersed throughout much of the comb.
It’s going to take a very well-designed experiment to convince me that bees rely largely on surface tension effects, as opposed to moulding the exquisite hexagons themselves. After all, the worker bees are rarely depicted as lazy.
Further reading:
Charles Darwin’s “On the origin of species”: is freely available on Archive.org and Project Gutenberg, for instance, and cheaply available in book form. Chapter VIII: Instinct, Cell-making instinct of the Hive-Bee, is the section referred to above.
After reading about Darwin’s experiments in his own words, I strongly recommend reading an account of Darwin’s honeycomb correspondence which includes some modern recreations of Darwin’s original experiments.
“On Growth and Form” by D’Arcy Thompson not only has a detailed history of the study of honeycomb geometry, but has many interesting facts about biological and geological shapes and their growth, as well as speculation about their root causes.
And on the pure mathematical geometry side, Fejes Tóth’s “What the bees know and what they do not know” gives the best overview of minimisation problems that bees’ honeycombs do solve, and then many more they do not solve.
Apiological part 2: Estimating nest volumes
Interesting article. For some reason it pleases me to think of bees as sensible, if not mathematically perfect.
Hey. Why were ei/3 and ei/2 is used for the Euler characteristic? I get that it will be a number of edges and vertices per face in the hexagon tiling but doesn’t it assume it will be the hexagon? Therefore, will it prove anything>
I hope to clarify that because I wanted to use a similar proof in my math paper :)